Gewone differentiaalvergelijkingen: Asymptotiek en stabiliteit
 Stabiliteit
Stabiliteit
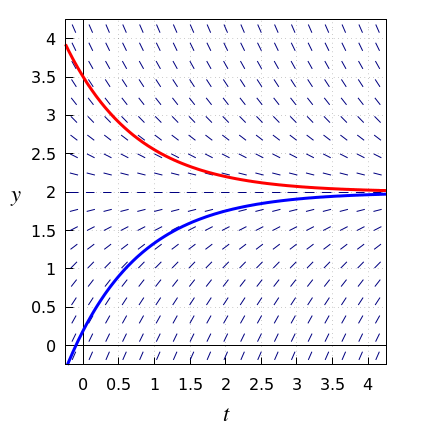
Veel voorkomend gedrag van een oplossing van een differentiaalvergelijking is dat deze een constante waarde nadert. De constante waarde is zelf ook een bijzondere oplossing, namelijk een evenwicht. We hebben al kort gekeken naar het gedrag van oplossing bij de logistische differentiaalvergelijking. Laten we hier als voorbeeld kijken naar de volgende differentiaalvergelijking van begrensde exponentiële groei: \[\frac{\dd y }{\dd t}=2-y\] In onderstaand lijnelementenveld zijn twee oplossingskrommen getekend die illustreren dat een oplossing van deze differentiaalvergelijking altijd \(y=2\) nadert voor grote waarden van \(t\). \(y(t)=2\) is zelf ook een oplossing van de differentiaalvergelijking en is een evenwicht, ook wel vast punt of steady state genoemd.
Het algemene geval is niet veel moeilijker. We bekijken dan de differentiaalvergelijking \[\frac{\dd y }{\dd t}=r\cdot (a-y)\] met positieve constanten \(r\) en \(a\). Er is één evenwicht en dat kunnen we vinden door de vergelijking \(\frac{\dd y }{\dd t}=0\) op te lossen. De oplossing van de lineaire vergelijking \(r\cdot (a-y)=0\) is eenvoudig te vinden en is \(y=a\).
Natuurlijk kun je ook de eisen over positiviteit van \(r\) en \(a\) loslaten.
Stabiliteit en asymptotiek van begrensde exponentiële groei We bekijken dan de differentiaalvergelijking \[\frac{\dd y }{\dd t}=r\cdot (a-y)\] met constanten \(r\neq 0\) en \(a\). De oplossing \[y=a\] is een evenwicht.
Als \(r>0\), dan nadert een oplossing van de differentiaalvergelijking altijd \(y=a\) voor grote waarden van \(t\). Met andere woorden, er is dan sprake van een aantrekkend evenwicht. We spreken ook wel van een stabiel evenwicht.
Als \(r<0\), dan wijkt elke oplossing van de differentiaalvergelijking ongelijk aan het evenwicht steeds meer van \(y=a\) af voor grote waarden van \(t\). Met andere woorden, er is dan sprake van een afstotend evenwicht. We spreken ook wel van een instabiel evenwicht.
Voorbeeld van een semistabiel evenwicht Behalve een stabiel of instabiel evenwicht, is er nog een derde variant, namelijk een semistabiel evenwicht, ook wel een half-stabiel evenwicht genoemd. In dit geval hangt het gedrag van een oplossing af van waar de oplossing zich bevindt ten opzichte van het evenwicht. De eerder bekeken GDV met exploderende oplossingen \[\frac{\dd y }{\dd t}=y^2\] illustreert dit.
Er is sprake van een evenwicht als \(y=0\). De algemene oplossing is een rationale functie van de vorm \[y(t)=\frac{1}{c-t}\] voor zekere constante \(c\). Maar in feite beschrijft dit functievoorschrift twee oplossingen: voor \(t<c\) hebben we een oplossing die wegloopt van het evenwicht in de loop der tijd en voor \(t>c\) hebben we een oplossing die naar het evenwicht toe gaat als de tijd verstrijkt. Anders geformuleerd in dit geval: een oplossingskromme met positieve functiewaarden loopt van het evenwicht vandaan in de loop der tijd en een oplossingskromme met negatieve functiewaarden nadert mettertijd het evenwicht. Het evenwicht is aan de ene kant een afstotend evenwicht, maar aan de andere kant een aantrekkend evenwicht.


