We hebben al gekeken naar het gedrag van oplossingen in de buurt van een evenwicht voor enkele autonome eerste-orde differentiaalvergelijkingen van de vorm

$$\frac{\dd y}{\dd t}=\varphi(y)$$ waarbij $\varphi$ een 'nette' functie is zodanig dat de eerder besproken stelling voor existentie en uniciteit opgaat. Meer specifiek eisen we in wat volgt dat de functie $\varphi$ een continue afgeleide heeft. We hebben bij de bestudering van het gedrag van oplossingen vooral het lijnelementenveld en integraalkrommen gebruikt om het gedrag in de buurt van evenwichten te verklaren. Grote vraag was steeds wat voor type evenwicht we hebben: afstotend of aantrekkend. We gaan dit stabiliteitsonderzoek nu systematisch aanpakken via

1. het tekenoverzicht van de functie $\varphi$.
2. lokale linearisatie van $\varphi$.

In deze theoriepagina behandelen we de eerste methode. Deze methode kan het eenvoudigst uitgelegd worden aan de hand van een concreet voorbeeld, zeg de GDV

$$\frac{\dd y}{\dd t}=y\,(y-1)(y-2)$$ De grafiek van de functie $\varphi(y)=y(y-1)(y-2)$ ziet er als volgt uit

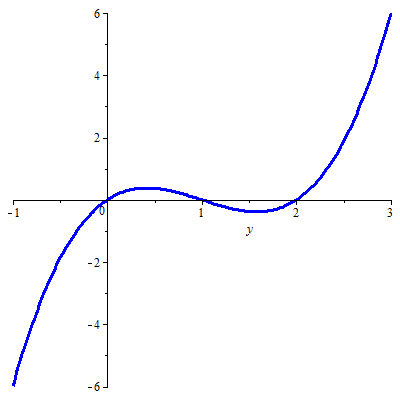
Aan deze grafiek kun je het volgende zien:

• De GDV heeft evenwichtsoplossingen $y=0$, $y=1$ en $y=2$
  omdat in deze waarden de functie $\varphi$ gelijk is aan $0$.
  
  
• $\displaystyle\left\{ \begin{array}{rl} \dfrac{\dd y}{\dd t}>0 & \text{voor alle punten }(t,y)\text{ met } 0\lt y\lt 1\text{ of }y>2\\ \dfrac{\dd y}{\dd t}<0 & \text{voor alle punten }(t,y)\text{ met } y<0\text{ of }1\lt y\lt 2\end{array}\right.$

Het tekenoverzicht van $\dfrac{\dd y}{\dd t}$, d.w.z. van het rechterlid van de GDV, is in onderstaande figuur aangegeven met plus- en mintekens. Het geeft aan in welke regio's van het $ty$-vlak een oplossingskromme daalt of stijgt.

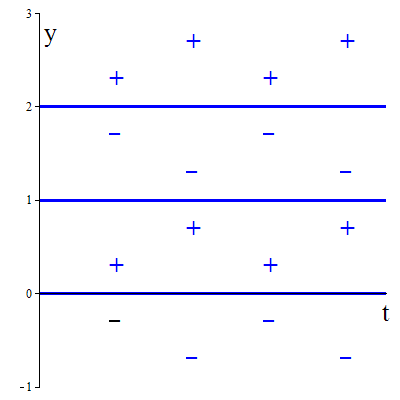
Vanwege de eis dat de functie $\varphi$ voldoende net is opdat de stelling van existentie en uniciteit opgaat, kunnen oplossingskrommen elkaar niet doorkruisen en kan in het bijzonder een stijgende of dalende oplossingskromme niet een evenwicht doorkruisen; een oplossingskromme kan dus alleen een evenwicht naderen. Bijvoorbeeld, de oplossingskromme door het punt $(0,1\tfrac{1}{2})$ is dalend en kan de lijn $y=1$ niet bereiken, maar wel onbeperkt naderen. Dus is de lijn $y=1$ een horizontale asymptoot van de oplossingskromme door $(0,1\tfrac{1}{2})$. De oplossingskromme door het punt $(0,\tfrac{1}{2})$ is stijgend en kan de lijn $y=1$ niet bereiken, maar wel onbeperkt naderen. Dus is de lijn $y=1$ een horizontale asymptoot van de oplossingskromme door $(0,\tfrac{1}{2})$. Meer algemeen: Alle oplossingskrommen door punten $(t,y)$ met $1\lt y\lt 2$ zijn dalend en hebben de lijn $y=1$ als asymptoot. Alle oplossingskrommen door punten $(t,y)$ met $0\lt y\lt 1$ zijn stijgend en hebben de lijn $y=1$ als asymptoot. Hieruit volgt dat $y=1$ een aantrekkend evenwicht is. Op dezelfde wijze blijken de evenwichten $y=0$ en $y=2$ afstotend te zijn.

In plaats van het tekenverloop van $\dfrac{\dd y}{\dd t}$ in een $(t,y)$-vlak te tekenen, gebruikt men ook vaak een getallenlijn waarin men met pijlen op deze lijn aangeeft of de helling van de oplossingskromme $y(t)$ van de GDV bij deze $y$-waarde positief of negatief is: een pijl naar rechts betekent een stijgende oplossingskromme en een pijl naar links betekent en dalende oplossingskromme. Voor de constructie van deze getallenlijn, die de toestandslijn van de GDV genoemd wordt (of in sommige boeken ook wel de naam faseportret gegeven wordt), hoeft men alleen maar te weten of de functiewaarden van $\varphi$ in een punt op de lijn positief, nul of negatief is. Onderstaande figuren illustreren de constructie van de toestandslijn, waarin open cirkels $\large\circ$ de afstotende evenwichten representeren en dichte cirkels $\large\bullet$ aantrekkend evenwichten aangeeft. Nota bene, dichte cirkels in toestandslijnen worden ook gebruikt om evenwichten aan te geven waarvan de stabiliteit onbekend is of niet te karakteriseren is als aantrekkend of afstotend.

Het eerste plaatje hieronder is de grafiek van de functie $\varphi(y)$ met op de horizontale as pijlen die aangeven of de functiewaarde positief of negatief is, dat wil zeggen, of oplossingskrommen op deze hoogte in het $(t,y)$-vlak stijgen of dalen. In een interval waar $\varphi(y)$ positief is, tekenen we een pijl naar rechts en in een interval waar $\varphi(y)$ negatief is, tekenen we een pijl naar links. Daar waar $\varphi(y)$ gelijk aan nul is (de evenwichten) bepaalt het soort pijlen links en rechts ervan wat voor evenwicht het is; bijvoorbeeld pijlen die naar elkaar toegericht zijn geven een aantrekkend evenwicht aan en wanneer de pijlen van elkaar af lopen hebben we te maken met een afstotend evenwicht.

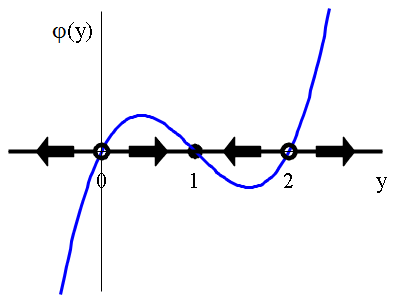
Bovenstaande figuur kan ingeperkt worden tot een 1-dimensionale figuur, de toestandslijn genaamd, die alle benodigde informatie over stabiliteit van oplossingen al bevat: dichte cirkels geven aantrekkende evenwichten aan, open cirkels geven afstotende evenwichten aan, en pijlen geven aan in welke richting oplossingskrommen gaan in de loop van de tijd.

In dit voorbeeld kwam geen semistabiel evenwicht voor, maar mocht je dat wel tegenkomen (bijvoorbeeld zoals in de GDV $\dfrac{\dd y}{\dd t}=y^2$), dan geef je dit aan met een half-dichte/half-open cirkel zoals ◐, waarbij de dichte kant zit aan de zijde waar oplossingen naar het evenwicht toegaan in de loop der tijd en de open kant aangeeft waar oplossingen mettertijd weglopen van het evenwicht.