Gewone differentiaalvergelijkingen: Lijnelementenveld en oplossingskrommen
 Lijnelementenveld
Lijnelementenveld
Voor een dynamisch systeem van eerste orde dat geschreven kan worden in de vorm \[\frac{\dd y}{\dd t}=\varphi(t,y)\] geldt voor elk punt \((t,y)\) op de grafiek van een oplossing dat de raaklijn helling \(\varphi(t,y)\) heeft. Om deze conditie te visualiseren teken je een kort lijnsegment met helling \(\varphi(t,y)\) gecentreerd in het punt \((t,y)\) (zie de linkerkant van onderstaande figuur). Dit lijnstuk heet een lijnelement in \((t,y)\). Als de functie \(y=y(t)\) een oplossing van de gegeven differentiaalvergelijking is door het punt \((t,y)\) dan raakt de grafiek van de functie aan het lijnelement in dat punt (zie de rechterkant van onderstaande figuur).
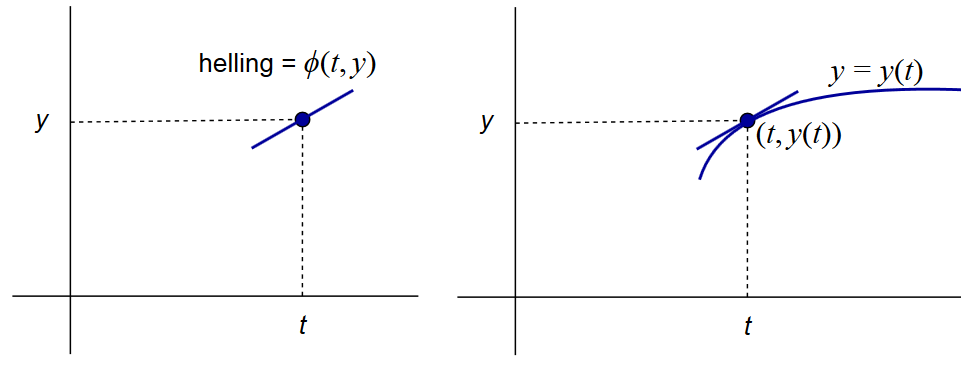
De linkerfiguur kun je tekenen voor willekeurige posities en de verzameling lijnelementen vormen dan een lijnelementenveld van de differentiaalvergelijking \(\dfrac{\dd y}{\dd t}=\varphi(t,y)\). Meestal wordt hiervoor een regelmatig rooster van punten gebruikt, maar dat hoeft niet.
We gaan een lijnelementenveld tekenen van de differentiaalvergelijking \[\frac{\dd y}{\dd t}=\frac{1}{2}(t-y)\] en we doen dit door lijnelementen te tekenen op roosterpunten met coördinaten \(t=0,1,2,3,4\) en \(y=0,1,2,3,4\). We pakken ruitjespapier en tekenen hierop de gekozen roosterpunten (de linkerkant van onderstaande figuur). Voor elk roosterpunt \((t,y)\) berekenen we de helling met de formule \(\frac{1}{2}(t-y)\). Onderstaande tabellen geeft alle waarden van de hellingen
\[\begin{array}{c|c|c|c|c|c} y=4 & -2 & -1.5 & -1 & -0.5 & 0 \\ \hline y=3 & -1.5 & -1 & -0.5 & 0 & 0.5
\\ \hline y=2 & -1 & -0.5 & 0 & 0.5 & 1\\ \hline y=1 & -0.5 & 0 & 0.5 & 1 & 1.5 \\ \hline y=0 & 0 & 0.5 & 1 & 1.5 & 2\\ \hline & t=0 & t=1 & t=2 & t=3 & t=4\end{array}\] Hiermee tekenen we op het ruitjespapier voor elk roosterpunt een kort lijnstukje gecentreerd in het roosterpunt en met de berekende helling (de lijnstukjes in de rechterkant van onderstaande figuur).
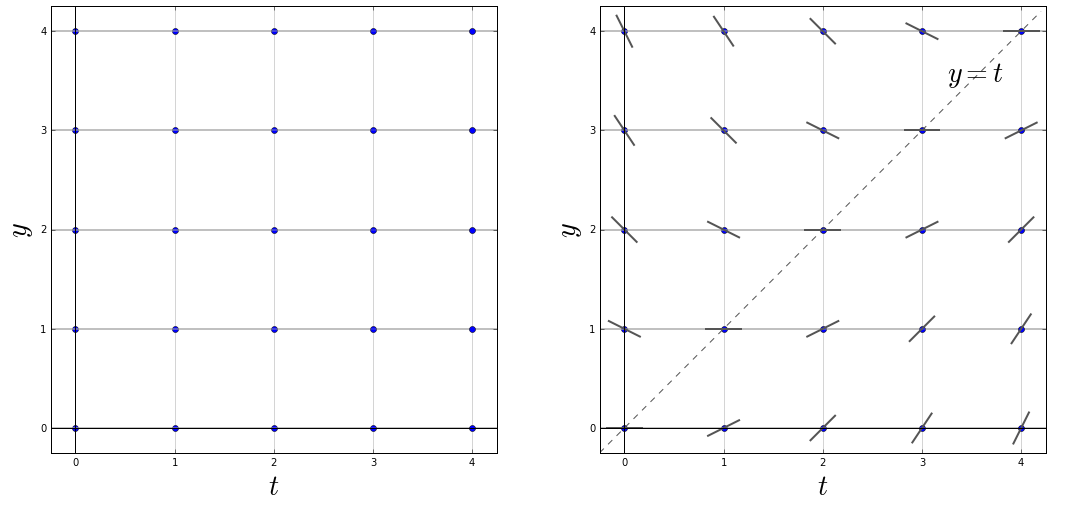
Het valt misschien op dat bij alle punten op de lijn \(y=x\) steeds de lijnelementen horizontaal zijn. Een verzameling van punten in het vlak waarin de lijnelementen dezelfde richting hebben noemt men een isocliene. De punten in het vlak waarin de lijnelementen horizontale richting vormen de verzameling van nul-isoclienen. in dit geval vormen ze de getekende lijn \(y=x\). Deze lijn verdeelt het lijnelementenveld in twee stukken: links boven deze lijn hebben alle lijnelementen een negatieve helling en rechts onder deze lijn hebben alle lijnelementen een positieve helling.


