Gewone differentiaalvergelijkingen: Lijnelementenveld en oplossingskrommen
 'Met de stroom meegaan'
'Met de stroom meegaan'
Een lijnelementenveld van een differentiaalvergelijking \(\dfrac{\dd y}{\dd t}=\varphi(t, y)\) kan een goede indruk geven van hoe de grafieken van oplossingen er uit zien omdat deze grafieken steeds lijnelementen moeten raken. Door een vloeiende kromme te tekenen die in elk punt raakt aan de lijnelementen krijg je een zogenaamde integraalkromme, de grafiek dus van een oplossing van de differentiaalvergelijking. Zo'n kromme heet ook wel oplossingskromme. We bekijken dit in twee eenvoudige voorbeelden.
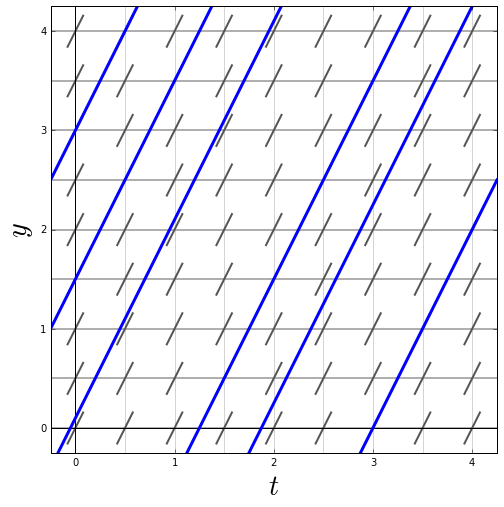
Voorbeeld 1 We bekijken de differentiaalvergelijking \[\frac{\dd y}{\dd t}=2\] In onderstaande figuur zijn in het getekende lijnelementenveld ook de grafieken van zes oplossingen getekend, namelijk van \(y=2t+c\) met van links naar rechts \(c=3, 1.5, 0.1, -2.5, 3.75, -6\). Alle oplossingen hebben grafieken met helling \(2\) want alle lijnelementen zijn evenwijdig en hebben helling \(2\). Je kunt een oplossing van de differentiaalvergelijking ook krijgen door steeds in de richting van lijnelementen mee te gaan.
Voorbeeld 2 In onderstaande figuur zie je links het lijnelementenveld van de differentiaalvergelijking \[\frac{\dd y}{\dd t}=t\] en rechts hetzelfde lijnelementenveld maar nu met de grafieken van oplossingen, namelijk die van \(y=\tfrac{1}{2}t^2+c\) met verschillende waarden van \(c\). Merk op dat de oplossingskrommen steeds in de richting van lijnelementen mee te gaan; dit is wat we bedoelen als we schrijven "met de stroom mee te gaan".
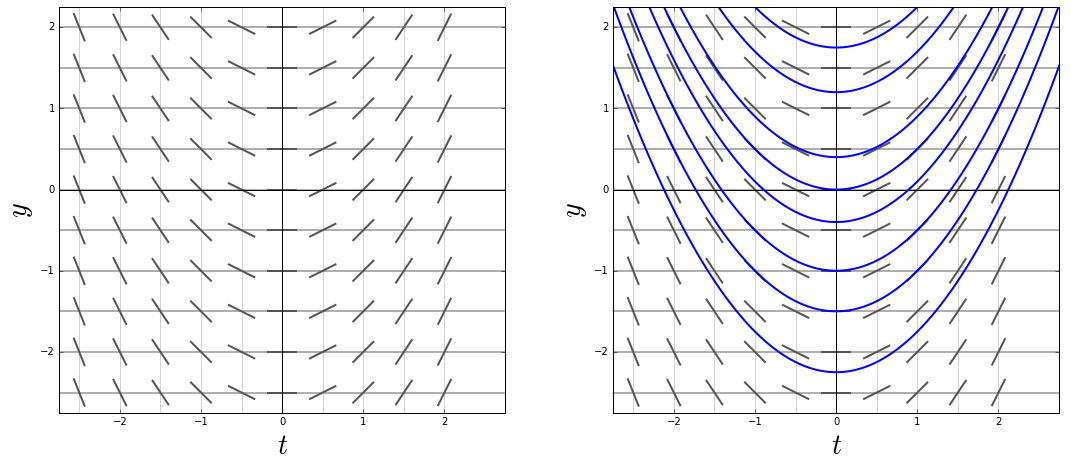
In dit lijnelementenveld zijn de isoclienen verticale lijnen die steiler zijn naarmate \(t\) meer van \(0\) verschilt. De nul-isocliene is de verticale as: deze scheidt lijnstukken met negatieve en positieve helling.


