Ordinary differential equations: Slope field and solution curves
Slope field vs direction field
In a slope field the lineal elements represent calculated slopes in points. This implies that that a vertical lineal element by definition does not exist. In case you allow such lineal elements we speak of a direction field and the integral curves can be closed curves in the plane or curves that can not be described by a single function. The following example illustrates this.
We consider the differential equation \[y\cdot \frac{\dd y}{\dd x}=-x\] The ODE can be rewritten in differential form as \[y\,\dd y+x\,\dd x=0\] The general implicit solution is \[y^2+x^2=c\] for some positive constant \(c\). This is the equation of a circle. With each implicit solution are associated two explicit solutions, i.e., solutions defined in the form of a function rule: \[ y(x)=\sqrt{c-x^2}\quad\text{or}\quad y(x)=-\sqrt{c-x^2}\] The integral curves are circles in the direction field (see figure below); in the slope field, the integral curves a semicircles.
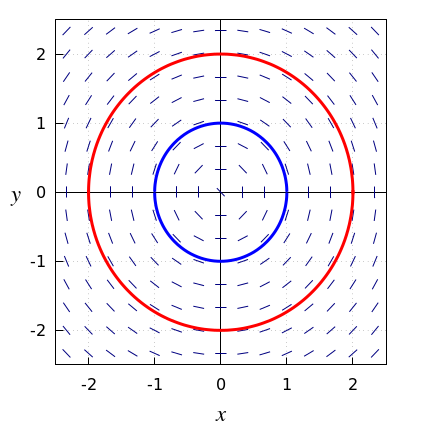
Phase portrait A slope field or direction field of a first-order ODE in which several solution curves have been plotted to give a good impression of the behaviour of solutions is called a phase portrait of the differential equation.
