Gewone differentiaalvergelijkingen: Lijnelementenveld en oplossingskrommen
Lijnelementenveld vs richtingsveld
In een lijnelementenveld geven de lijnstukjes berekende hellingen in punten weer. Dit impliceert dat dat verticale lijnelementen per definitie niet bestaan. Als je dergelijke lijnelementen wel toestaat dan spreken we van een richtingsveld en integraalkrommen kunnen dan ook gesloten krommen in het vlak of krommen die niet door één functie beschreven kunnen worden. In onderstaand voorbeeld wordt dit geïllustreerd.
We bekijken de differentiaalvergelijking \[y\cdot \frac{\dd y}{\dd x}=-x\] In differentiaalvorm is deze GDV te herschrijven als \[y\,\dd y+x\,\dd x=0\] De algemene impliciete oplossing is \[y^2+x^2=c\] voor zekere positieve constante \(c\). Dit is de vergelijking van een cirkel. Bij een impliciete oplossing horen twee expliciete oplossingen, dus oplossingen in de vorm van een functievoorschrift: \[ y(x)=\sqrt{c-x^2}\quad\text{of}\quad y(x)=-\sqrt{c-x^2}\] In het richtingsveld zijn de integraalkrommen cirkels (zie onderstaande figuur); in het lijnelementenveld zijn de integraalkrommen half-cirkels.
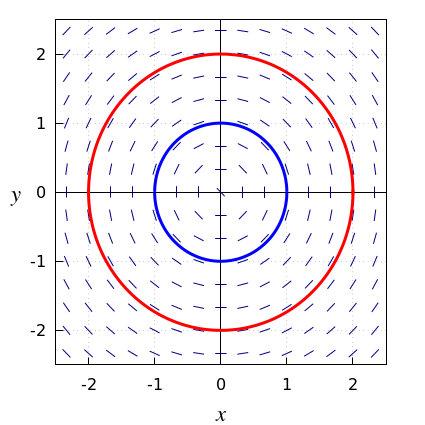
Faseportret Een lijnelementenveld of richtingsveld van een eerste-orde GDV met hierin verschillende oplossingskrommen getekend zodat een goed beeld gegeven wordt van het gedrag van oplossingen noemt men ook wel een faseportret van de differentiaalvergelijking.
