Worked-out solution

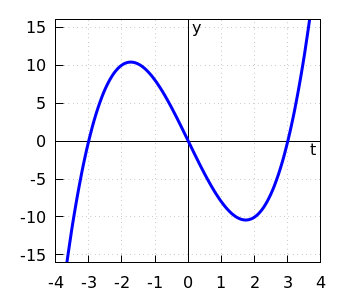
1. We can factorise the right-hand side of the differential equation:\[\begin{aligned} \varphi(y) &=-9y+y^3\\ &= y\,(y^2-9) \\ &= y\,(y-3)\,(y+3)\end{aligned}\] So \(\varphi\) is a cubic polynomial with zeros \(-3\), \(0\) and \(3\). The equilibria of the differential equation are in increasing ordering \(y=-3\), \(y=0\) and \(y=3\). We compute the derivative \(\dfrac{\dd \varphi}{\dd y}\): \[\varphi'(y)=-9+3y^2=3(y^2-3)\] So \(\varphi'(y)=0\) if and only if \(y^2-3=0\), or \(y=\pm\sqrt{3}\). Because \(\dfrac{\dd^2\varphi}{\dd y^2}=6y\), we have \(\varphi''(\sqrt{3})>0\) and \(\varphi''(-\sqrt{3})<0\), and thus we know that \(y=\sqrt{3}\) is a maximum of \(\varphi\), \(y=\sqrt{3}\) is a minimum of \(\varphi\), and that \(y=0\) is an inflection point. We know enough to sketch the graph of \(\varphi\):

   

2. We determine the nature of the equilibria by local linearisation. For this we need again the derivative \(\dfrac{\dd \varphi}{\dd y}\): \[\varphi'(y)=3(y^2-3)\] So \[\begin{aligned} \varphi'(0)=-9<0 \quad &\text{so that}\quad y=0\text{ is an attractor and}\\ \varphi'(\pm\sqrt{3})=18>0\quad &\text{so that}\quad y=\pm\sqrt{3}\text{ is a repeller.}\end{aligned}\] This is consistent with the sign pattern of \(\varphi\)

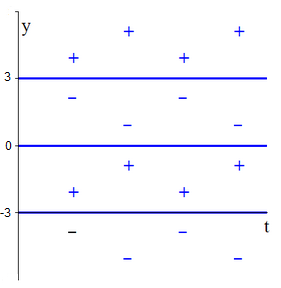   and the phase line

   

3. If \(y(0)=0.1\), then the initial value belongs to the interval \((0,3)\) within which the sign of the right- hand side of the differential equation is negative. This is a descending solution curve that approaches \(0\) for large \(t\); So \(\displaystyle \lim_{t\rightarrow\infty} y(t)=0\) if \(y(0)=0.1\).

Worked-out solution

1. In order to find the equilibria of the differential equation we must solve the equation \(\varphi(x)=0\): \[\begin{aligned} \varphi(x)=0 &\iff\frac{2x^2}{1+x^3}-x=0\\ &\iff \frac{2x^2}{1+x^3}=x \\ &\iff x=0\quad\text{or}\quad\frac{2x}{1+x^3}\end{aligned}\] We work out the second equation: \[\begin{aligned}1+x^3=2x &\iff x^3-2x+1=0 \\ &\iff (x-1)(x^2+x-1)=0 \\ &\iff x=1\quad\text{or}\quad x=\dfrac{-1\pm\sqrt{5}}{2}\end{aligned}\] There exist three nonnegative equilibria of the differential equation; they are in increasing ordering \(x=0\), \(x=\dfrac{-1+\sqrt{5}}{2}\) and \(x=1\).
2. We determine the nature of the equilibria by local linearisation. For this we need the derivative \(\dfrac{\dd \varphi}{\dd x}\). With the quotient rule for differentiation we get: \[\begin{aligned}\varphi'(x)&=\frac{4x(1+x^3)-2x^2\cdot 3x^2}{1+x^3)^2} -1\\ \\ &= \frac{4x-4x^4}{1+x^3)^2}-1\\ \\ &= \frac{2x(2-x^3)}{1+x^3)^2}-1\end{aligned}\] So: \[\begin{aligned} \varphi'(0)=-1<0 \quad &\text{so that}\quad x=0\text{ is an attractor,}\\ \varphi'(1)=\frac{1}{2}<0 \quad &\text{so that}\quad x=1\text{ is an attractor, and} \\ \varphi'\left(\tfrac{-1}{2}+\tfrac{1}{2}\sqrt{5}\right)>0 \quad &\text{so that}\quad x=\tfrac{-1}{2}+\tfrac{1}{2}\sqrt{5}\text{ is a repeller.}\end{aligned}\] This is consistent with the sign pattern of \(\varphi\) and the phase line
   

   

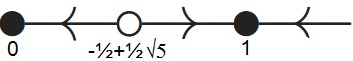
3. If \(x(0)=0.001\), then the initial value belongs to the interval \((0,-\tfrac{1}{2}+\tfrac{1}{2}\sqrt{5})\) within which the sign of the right-hand side of the differential equation is negative. This is a descending solution curve that approaches \(0\) for large \(t\). So \(\displaystyle \lim_{t\rightarrow\infty} x(t)=0\) if \(x(0)=0.001\).
4. If \(x(0)=0.8\), then the initial value belongs to the interval \((-\tfrac{1}{2}+\tfrac{1}{2}\sqrt{5}, 1)\) within which the sign of the right-hand side of the differential equation is positive. This is a descending solution curve that approaches \(1\) for large \(t\). So \(\displaystyle \lim_{t\rightarrow\infty} x(t)=1\) if \(x(0)=0.8\).
5. If \(x(0)=1\), then the initial value is an equilibrium value. So \(\displaystyle \lim_{t\rightarrow\infty} x(t)=1\) if \(x(0)=1\).

Worked-out solution

1. In order to find the equilibria we must solve the equation \(\varphi(y)=0\): \[\begin{aligned} \varphi(y)=0 &\iff \;\;-15+8y-y^2=0\\ &\iff -(y-3)(y-5) =0\end{aligned}\] There are two equilibria of the differential equation; they are in increasing ordering \(y=3\) and \(y=5\) The function \(\varphi\) is a mountain parabola, and thus is \(\varphi(y)\) positive for \(y\) in the interval (0,3), and a negative elsewhere. This gives the following phase line:
   

   

   We can verify the nature of the equilibria by the method of local linearisation: \(\varphi'(y)=8-2y\) and therefore: \[\begin{aligned} \varphi'(3)=\phantom{-}2>0\quad &\text{so that}\quad y=3\text{ is a repeller and}\\ \varphi'(5)=-2<0\quad &\text{zodat}\quad y=5\text{ is an attractor.}\end{aligned}\] Furthermore: \[\begin{aligned} \lim_{t\rightarrow \infty} y(t)=-\infty &\;\;\text{ if }\;y(0)<3\\ \lim_{t\rightarrow \infty} y(t)=3\;\;\;\;\, &\;\;\text{ if }\;y(0)=3 \\ \lim_{t\rightarrow \infty} y(t)=5\;\;\;\;\, &\;\;\text{ if }\;y(0)>3\end{aligned}\]
   
   
2. In order to find the equilibria we must solve the equation \(\varphi(y)=0\): \[\begin{aligned} \varphi(y)=0 &\iff \;\;\;\;-4+5y-y^2=0\\ &\iff -(y-1)(y-4) =0\end{aligned}\] There are two equilibria of the differential equation; they are in increasing ordering \(y=1\) and \(y=4\) The function \(\varphi\) is a mountain parabola, and thus is \(\varphi(y)\) positive for \(y\) in the interval (1,4), and a negative elsewhere. This gives the following phase line:
   

   

   We can verify the nature of the equilibria by the method of local linearisation: \(\varphi'(y)=5-2y\) and therefore: \[\begin{aligned} \varphi'(1)=\phantom{-}3>0\quad &\text{so that}\quad y=1\text{ is a repeller and}\\ \varphi'(4)=-3<0\quad &\text{so that}\quad y=4\text{ is an attractor.}\end{aligned}\] Furthermore: \[\begin{aligned} \lim_{t\rightarrow \infty} y(t)=-\infty &\;\;\text{ if }\;y(0)<1\\ \lim_{t\rightarrow \infty} y(t)=1\;\;\;\;\, &\;\;\text{ if }\;y(0)=1 \\ \lim_{t\rightarrow \infty} y(t)=4\;\;\;\;\, &\;\;\text{ if }\;y(0)>1\end{aligned}\]
   
   
3. In order to find the equilibria we must solve the equation \(\varphi(y)=0\): \[\begin{aligned} \varphi(y)=0 &\iff \;\; -y(y^2+y-6)=0\\ &\iff -y\,(y+3)(y-2) =0\end{aligned}\] There exist three equilibria of the differential equation; they are in increasing ordering \(y=-3\), \(y=0\), and \(y=2\). We can verify the nature of the equilibria by the method of local linearisation: \(\varphi'(y)=-3y^2-2y+6\) and therefore: \[\begin{aligned} \varphi'(-3)=-15<0 \quad &\text{so that}\quad y=-3\text{ is an attractor,}\\ \varphi'(0)=\phantom{-1}6>0 \quad &\text{so that}\quad y=0\text{ is a repeller, and} \\ \varphi'(2)=-10<0 \quad &\text{so that}\quad y=2\text{ is an attractor.}\end{aligned}\] This gives the following phase line:
   

   

   Furthermore: \[\begin{aligned} \lim_{t\rightarrow \infty} y(t)=-3 &\;\;\text{ if }\;y(0)<0\\ \lim_{t\rightarrow \infty} y(t)=0\;\;\,\, &\;\;\text{ if }\;y(0)=0 \\ \lim_{t\rightarrow \infty} y(t)=2\;\;\,\, &\;\;\text{ if }\;y(0)>0\end{aligned}\]
   
   
4. In order to find the equilibria we must solve the equation \(\varphi(y)=0\): \[\begin{aligned} \varphi(y)=0 &\iff \;\;8y-y^2=0\\ &\iff y\,(8-y^2) =0\\ &\iff y\,(2\sqrt{2}-y)(2\sqrt{2}+y) =0 \end{aligned}\] There exist three equilibria of the differential equation; they are in increasing ordering \(y=-2\sqrt{2}\), \(y=0\), and \(y=2\sqrt{2}\). We can verify the nature of the equilibria by the method of local linearisation: \(\varphi'(y) =8-3y^2\) and therefore: \[\begin{aligned} \varphi'(-1\sqrt{2})=-16<0 \quad &\text{so that}\quad y=-2\sqrt{2}\text{ is an attractor,}\\ \varphi'(0)=\phantom{-1}8>0 \quad &\text{so that}\quad y=0\text{ is a repeller, and} \\ \varphi'(2)=-10<0 \quad &\text{so that}\quad y=2\sqrt{2}\text{ is an attractor.}\end{aligned}\] This gives the following phase line:
   

   

   Furthermore: \[\begin{aligned} \lim_{t\rightarrow \infty} y(t)=-2\sqrt{2} &\;\;\text{ if }\;y(0)<0\\ \lim_{t\rightarrow \infty} y(t)=0\;\;\;\;\;\;\;\, &\;\;\text{ if }\;y(0)=0 \\ \lim_{t\rightarrow \infty} y(t)=2\sqrt{2}\;\;\,\, &\;\;\text{ if }\;y(0)>0\end{aligned}\]
   
   
5. In order to find the equilibria we must solve the equation \(\varphi(y)=0\): \[\begin{aligned} \varphi(y)=0 &\iff \dfrac{3y^2}{2+y^2}-y=0\\ \\ &\iff \dfrac{3y^2}{2+y^2}=y\\ \\ &\iff y =0\quad\text{of}\quad \dfrac{3y}{2+y^2}= 1\end{aligned}\] We work out the second equation: \[\begin{aligned} \dfrac{3y}{2+y^2}=1 &\iff 3y=2+y^2 \\ &\iff y^2-3y+2=0\\ &\iff (y-2)(y-1)=0\end{aligned}\] There exist three equilibria of the differential equation; they are in increasing ordering \(y=0\), \(y=1\), and \(y=2\). We can verify the nature of the equilibrium by the method of local linearisation: the quotient rule for differentiation gives \[\begin{aligned}\varphi'(y) &=\dfrac{6y\cdot (2+y^2)-3y^2\cdot 2y}{(2+y^2)^2}-1 \\ \\ &= \dfrac{12y}{(2+y^2)^2}-1\end{aligned}\] So: \[\begin{aligned} \varphi'(0)=\,-1<0 \quad &\text{so that}\quad y=0\text{ is an attractor,}\\ \varphi'(1)=\phantom{-}\tfrac{1}{3}>0 \quad &\text{so that}\quad y=1\text{ is a repeller, and} \\ \varphi'(2)=-\tfrac{1}{3}<0 \quad &\text{so that}\quad y=2\text{ is an attractor.}\end{aligned}\] This gives the following phase line:
   

   

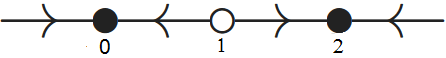
   Furthermore: \[\begin{aligned} \lim_{t\rightarrow \infty} y(t)=0 &\;\;\text{ if }\;y(0)<1\\ \lim_{t\rightarrow \infty} y(t)=1 &\;\;\text{ if }\;y(0)=1 \\ \lim_{t\rightarrow \infty} y(t)=2 &\;\;\text{ if }\;y(0)>1\end{aligned}\]