Uitwerking

1. We kunnen de rechterkant van de differentiaalvergelijking ontbinden in factoren: $$\begin{aligned} \varphi(y) &=-9y+y^3\\ &= y\,(y^2-9) \\ &= y\,(y-3)\,(y+3)\end{aligned}$$ Dus is $\varphi$ een derdegraadsveelterm met nulpunten $-3$, $0$ en $3$. De evenwichten van de differentiaalvergelijking zijn dus $y=-3$, $y=0$ en $y=3$. We doen een beperkt functieonderzoek en rekenen daarvoor de afgeleide $\dfrac{\dd \varphi}{\dd y}$ uit: $$\varphi'(y)=-9+3y^2=3(y^2-3)$$ Dan geldt dat $\varphi'(y)=0$ dan en slechts dan als $y^2-3=0$, oftewel als $y=\pm\sqrt{3}$. Omdat $\dfrac{\dd^2\varphi}{\dd y^2}=6y$, en dus $\varphi''(\sqrt{3})>0$ en $\varphi''(-\sqrt{3})<0$, weten we dat $y=\sqrt{3}$ een maximum van $\varphi$ is, $y=\sqrt{3}$ een minimum van $\varphi$ is, en dat $y=0$ een buigpunt is. We weten nu voldoende om een schets van de grafiek van $\varphi$ te maken:

   

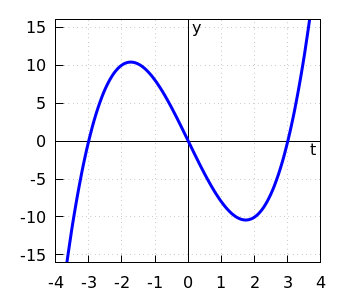
2. We bepalen de aard van de evenwichten door lokale linearisatie. Hiervoor hebben we weer de afgeleide $\dfrac{\dd \varphi}{\dd y}$ nodig: $$\varphi'(y)=3(y^2-3)$$ Dus: $$\begin{aligned} \varphi'(0)=-9<0 \quad &\text{zodat}\quad y=0\text{ een aantrekkend evenwicht is en}\\ \varphi'(\pm\sqrt{3})=18>0\quad &\text{zodat}\quad y=\pm\sqrt{3}\text{ een afstotend evenwicht is.}\end{aligned}$$ Dit is in overeenstemming met het tekenoverzicht van $\varphi$

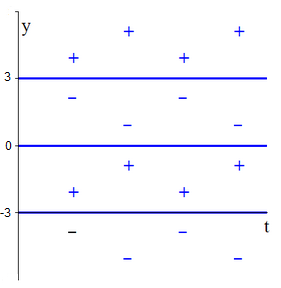   en met het faseportret

   

3. Als $y(0)=0.1$, dan zit de startwaarde in het interval $(0,3)$ waarbinnen het teken van de rechterkant van de differentiaalvergelijking negatief is. Dit is een dalende oplossingskromme die voor grote $t$ naar $0$ nadert; dus $\displaystyle \lim_{t\rightarrow\infty} y(t)=0$.

Uitwerking

1. Om de evenwichten van de differentiaalvergelijking te vinden moeten we de vergelijking $\varphi(x)=0$ oplossen $$\begin{aligned} \varphi(x)=0 &\iff\frac{2x^2}{1+x^3}-x=0\\ &\iff \frac{2x^2}{1+x^3}=x \\ &\iff x=0\quad\text{of}\quad\frac{2x}{1+x^3}\end{aligned}$$ We werken de tweede vergelijking verder uit: $$\begin{aligned}1+x^3=2x &\iff x^3-2x+1=0 \\ &\iff (x-1)(x^2+x-1)=0 \\ &\iff x=1\quad\text{of}\quad x=\dfrac{-1\pm\sqrt{5}}{2}\end{aligned}$$ Er zijn dus drie niet-negatieve evenwichten van de differentiaalvergelijking; in opklimmende volgorde zijn het $x=0$, $x=\dfrac{-1+\sqrt{5}}{2}$ en $x=1$.
2. We bepalen de aard van de evenwichten door lokale linearisatie. Hiervoor hebben we de afgeleide $\dfrac{\dd \varphi}{\dd x}$ nodig. Met de quotiëntregel voor differentiëren krijgen we : $$\begin{aligned}\varphi'(x)&=\frac{4x(1+x^3)-2x^2\cdot 3x^2}{(1+x^3)^2} -1\\ \\ &= \frac{4x-4x^4}{(1+x^3)^2}-1\\ \\ &= \frac{2x(2-x^3)}{(1+x^3)^2}-1\end{aligned}$$ Dus: $$\begin{aligned} \varphi'(0)=-1<0 \quad &\text{zodat}\quad x=0\text{ een aantrekkend evenwicht is,}\\ \varphi'(1)=\frac{1}{2}<0 \quad &\text{zodat}\quad x=1\text{ een aantrekkend evenwicht is en} \\ \varphi'\left(\tfrac{-1}{2}+\tfrac{1}{2}\sqrt{5}\right)>0 \quad &\text{zodat}\quad x=\tfrac{-1}{2}+\tfrac{1}{2}\sqrt{5}\text{ een afstotend evenwicht is.}\end{aligned}$$ Dit is in overeenstemming met het tekenoverzicht van $\varphi$ en het daaruit af te leiden faseportret
   

   

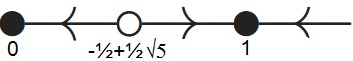
3. Als $x(0)=0.001$, dan zit de beginwaarde in het interval $(0,-\tfrac{1}{2}+\tfrac{1}{2}\sqrt{5})$ waarbinnen het teken van de rechterkant van de differentiaalvergelijking negatief is. Dit is een dalende oplossingskromme die voor grote $t$ naar $0$ nadert; dus $\displaystyle \lim_{t\rightarrow\infty} x(t)=0$ als $x(0)=0.001$.
4. Als $x(0)=0.8$, dan zit de beginwaarde in het interval $(-\tfrac{1}{2}+\tfrac{1}{2}\sqrt{5}, 1)$ waarbinnen het teken van de rechterkant van de differentiaalvergelijking positief is. Dit is een stijgende oplossingskromme die voor grote $t$ naar $1$ nadert; dus $\displaystyle \lim_{t\rightarrow\infty} x(t)=1$ als $x(0)=0.8$.
5. Als $x(0)=1$, dan is de beginwaarde een evenwichtswaarde; dus $\displaystyle \lim_{t\rightarrow\infty} x(t)=1$ als $x(0)=1$.

Uitwerking

1. Om de evenwichten te vinden moeten we de vergelijking $\varphi(y)=0$ oplossen: $$\begin{aligned} \varphi(y)=0 &\iff \;\;-15+8y-y^2=0\\ &\iff -(y-3)(y-5) =0\end{aligned}$$ Er zijn dus twee evenwichten van de differentiaalvergelijking; in opklimmende volgorde zijn het $y=3$ en $y=5$ De functie $\varphi$ een bergparabool en dus is $\varphi(y)$ positief voor $y$ in het interval (0,3) en negatief daarbuiten. Dit geeft het onderstaande faseportret:
   

   

   We kunnen de aard van de evenwichten verifiëren via de methode van lokale linearisatie: $\varphi'(y)=8-2y$ en dus: $$\begin{aligned} \varphi'(3)=\phantom{-}2>0\quad &\text{zodat}\quad y=3\text{ een afstotend evenwicht is en}\\ \varphi'(5)=-2<0\quad &\text{zodat}\quad y=5\text{ een aantrekkend evenwicht is.}\end{aligned}$$ Verder geldt dan: $$\begin{aligned} \lim_{t\rightarrow \infty} y(t)=-\infty &\;\;\text{ als }\;y(0)<3\\ \lim_{t\rightarrow \infty} y(t)=3\;\;\;\;\, &\;\;\text{ als }\;y(0)=3 \\ \lim_{t\rightarrow \infty} y(t)=5\;\;\;\;\, &\;\;\text{ als }\;y(0)>3\end{aligned}$$
   
   
2. Om de evenwichten te vinden moeten we de vergelijking $\varphi(y)=0$ oplossen $$\begin{aligned} \varphi(y)=0 &\iff \;\;\;\;-4+5y-y^2=0\\ &\iff -(y-1)(y-4) =0\end{aligned}$$ Er zijn dus twee evenwichten van de differentiaalvergelijking; in opklimmende volgorde zijn het $y=1$ en $y=4$ Het gaat om een bergparabool en dus is $\varphi(y)$ positief voor $y$ in het interval (1,4) en negatief daarbuiten. Dit geeft het onderstaande faseportret:
   

   

   We kunnen de aard van de evenwichten verifiëren via de methode van lokale linearisatie: $\varphi'(y)=5-2y$ en dus: $$\begin{aligned} \varphi'(1)=\phantom{-}3>0\quad &\text{zodat}\quad y=1\text{ een afstotend evenwicht is en}\\ \varphi'(4)=-3<0\quad &\text{zodat}\quad y=4\text{ een aantrekkend evenwicht is.}\end{aligned}$$ Verder geldt dan: $$\begin{aligned} \lim_{t\rightarrow \infty} y(t)=-\infty &\;\;\text{ als }\;y(0)<1\\ \lim_{t\rightarrow \infty} y(t)=1\;\;\;\;\, &\;\;\text{ als }\;y(0)=1 \\ \lim_{t\rightarrow \infty} y(t)=4\;\;\;\;\, &\;\;\text{ als }\;y(0)>1\end{aligned}$$
   
   
3. Om de evenwichten te vinden moeten we de vergelijking $\varphi(y)=0$ oplossen: $$\begin{aligned} \varphi(y)=0 &\iff \;\; -y(y^2+y-6)=0\\ &\iff -y\,(y+3)(y-2) =0\end{aligned}$$ Er zijn dus drie evenwichten van de differentiaalvergelijking; in opklimmende volgorde zijn het $y=-3$, $y=0$ en $y=2$. We kunnen de aard van de evenwichten verifiëren via de methode van lokale linearisatie: $\varphi'(y)=-3y^2-2y+6$ en dus: $$\begin{aligned} \varphi'(-3)=-15<0 \quad &\text{zodat}\quad y=-3\text{ een aantrekkend evenwicht is,}\\ \varphi'(0)=\phantom{-1}6>0 \quad &\text{zodat}\quad y=0\text{ een afstotend evenwicht is en} \\ \varphi'(2)=-10<0 \quad &\text{zodat}\quad y=2\text{ een aantrekkend evenwicht is.}\end{aligned}$$ Dit geeft het onderstaande faseportret:
   

   

   Verder geldt dan: $$\begin{aligned} \lim_{t\rightarrow \infty} y(t)=-3 &\;\;\text{ als }\;y(0)<0\\ \lim_{t\rightarrow \infty} y(t)=0\;\;\,\, &\;\;\text{ als }\;y(0)=0 \\ \lim_{t\rightarrow \infty} y(t)=2\;\;\,\, &\;\;\text{ als }\;y(0)>0\end{aligned}$$
   
   
4. Om de evenwichten te vinden moeten we de vergelijking $\varphi(y)=0$ oplossen: $$\begin{aligned} \varphi(y)=0 &\iff \;\;8y-y^2=0\\ &\iff y\,(8-y^2) =0\\ &\iff y\,(2\sqrt{2}-y)(2\sqrt{2}+y) =0 \end{aligned}$$ Er zijn dus drie evenwichten van de differentiaalvergelijking; in opklimmende volgorde zijn het $y=-2\sqrt{2}$, $y=0$ en $y=2\sqrt{2}$. We kunnen de aard van de evenwichten verifiëren via de methode van lokale linearisatie: $\varphi'(y) =8-3y^2$ en dus: $$\begin{aligned} \varphi'(-1\sqrt{2})=-16<0 \quad &\text{zodat}\quad y=-2\sqrt{2}\text{ een aantrekkend evenwicht is,}\\ \varphi'(0)=\phantom{-1}8>0 \quad &\text{zodat}\quad y=0\text{ een afstotend evenwicht is en} \\ \varphi'(2)=-10<0 \quad &\text{zodat}\quad y=2\sqrt{2}\text{ een aantrekkend evenwicht is.}\end{aligned}$$ Dit geeft het onderstaande faseportret:
   

   

   Verder geldt dan: $$\begin{aligned} \lim_{t\rightarrow \infty} y(t)=-2\sqrt{2} &\;\;\text{ als }\;y(0)<0\\ \lim_{t\rightarrow \infty} y(t)=0\;\;\;\;\;\;\;\, &\;\;\text{ als }\;y(0)=0 \\ \lim_{t\rightarrow \infty} y(t)=2\sqrt{2}\;\;\,\, &\;\;\text{ als }\;y(0)>0\end{aligned}$$
   
   
5. Om de evenwichten te vinden moeten we de vergelijking $\varphi(y)=0$ oplossen: $$\begin{aligned} \varphi(y)=0 &\iff \dfrac{3y^2}{2+y^2}-y=0\\ \\ &\iff \dfrac{3y^2}{2+y^2}=y\\ \\ &\iff y =0\quad\text{of}\quad \dfrac{3y}{2+y^2}= 1\end{aligned}$$ We werken de tweede vergelijking verder uit:: $$\begin{aligned} \dfrac{3y}{2+y^2}=1 &\iff 3y=2+y^2 \\ &\iff y^2-3y+2=0\\ &\iff (y-2)(y-1)=0\end{aligned}$$ Er zijn dus drie evenwichten van de differentiaalvergelijking; in opklimmende volgorde zijn het $y=0$, $y=1$ en $y=2$. We kunnen de aard van de evenwichten verifiëren via de methode van lokale linearisatie: $$\begin{aligned}\varphi'(y) &=\dfrac{6y\cdot (2+y^2)-3y^2\cdot 2y}{(2+y^2)^2}-1 \\ \\ &= \dfrac{12y}{(2+y^2)^2}-1\end{aligned}$$ en dus: $$\begin{aligned} \varphi'(0)=\,-1<0 \quad &\text{zodat}\quad y=0\text{ een aantrekkend evenwicht is,}\\ \varphi'(1)=\phantom{-}\tfrac{1}{3}>0 \quad &\text{zodat}\quad y=1\text{ een afstotend evenwicht is en} \\ \varphi'(2)=-\tfrac{1}{3}<0 \quad &\text{zodat}\quad y=2\text{ een aantrekkend evenwicht is.}\end{aligned}$$ Dit geeft het onderstaande faseportret:
   

   

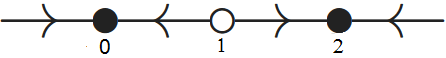
   Verder geldt dan: $$\begin{aligned} \lim_{t\rightarrow \infty} y(t)=0 &\;\;\text{ als }\;y(0)<1\\ \lim_{t\rightarrow \infty} y(t)=1 &\;\;\text{ als }\;y(0)=1 \\ \lim_{t\rightarrow \infty} y(t)=2 &\;\;\text{ als }\;y(0)>1\end{aligned}$$