Bifurcatiepunt We kijken nogmaals naar de differentiaalvergelijking van exponentiële groei met relatieve groeisnelheidsconstante $r$: $$\frac{\dd y}{\dd t}=r\cdot y$$ Het gedrag van de oplossingen hangt af van het teken van $r$: als $r<0$, dan is er sprake van exponentieel verval en is het evenwicht $y=0$ aantrekkend; als $r>0$, dan is er sprake van exponentiële groei en is het evenwicht $y=0$ afstotend. Deze verandering van gedrag van rondom een evenwicht heet een bifurcatie en de parameterwaarde waarbij dit gebeurt, in dit geval $r=0$, noemen we een bifurcatiewaarde.

In dit voorbeeld gaat het om de differentiaalvergelijking van exponentiële groei, maar dit spel kan natuurlijk voor elke differentiaalvergelijking met een parameter in de definitie worden gespeeld.

Bifurcatiediagram Laten we als tweede voorbeeld van een differentiaalvergelijking met een parameter die bifurcaties heeft kijken naar $$\frac{\dd y}{\dd t}=y^2+b\cdot y+1$$ Om de evenwichten te bepalen moet we de nulpunten van de kwadratische vergelijking $$y^2+b\cdot y+1=0$$ in $y$ uitrekenen. Maar dit hangt af van het teken van de discriminant $D=b^2-4$:

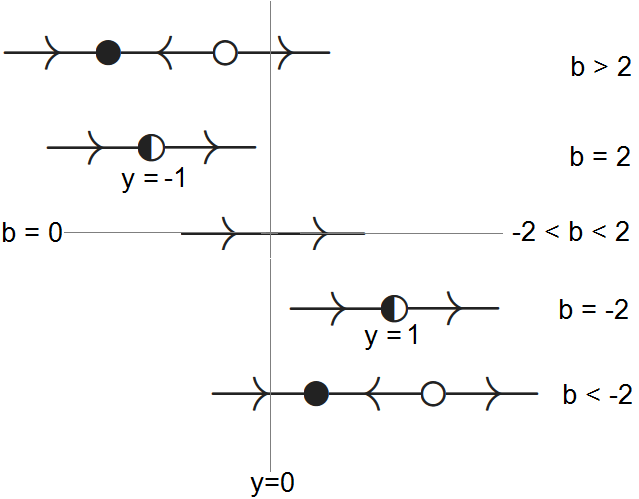
• Als $D<0$, oftewel als $-2<b<2$, dan is er geen nulpunt en dus ook geen evenwicht van de GDV.
• Als $D=0$, oftewel in het geval $b=-2$ of $b=2$, dan is er maar één evenwicht, namelijk $y=1$ of $y=-1$.
• Als $D>0$, dan zijn er twee nulpunten en dus ook twee evenwichten, namelijk $y=\dfrac{-b\pm\sqrt{b^2-4}}{2}$.

De aard van deze evenwichten is ook te bepalen m.b.v. standaardmethoden voor stabiliteitsonderzoek:

• Als $D=0$, oftewel in het geval $b=-2$ of $b=2$, dan hebben we als GDV $\dfrac{\dd y}{\dd t}=(y-1)^2$ of $\dfrac{\dd y}{\dd t}=(y+1)^2$. In beide gevallen is het rechterlid van de GDV een kwadraat. We hebben dan te maken met een semistabiel evenwicht met toestandslijn
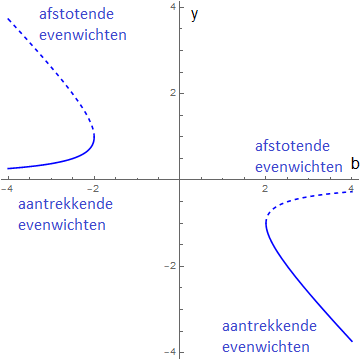
• Als $D>0$ dan is de rechterkant van de GDV een dalparabool met twee nulpunten. Tussen deze twee nulpunten is de functiewaarde negatief en in deze regio dalen oplossingskrommen. Buiten dit binnengebied is de functiewaarde van de kwadratische functie positief en dus stijgen in dit gebied oplossingskrommen. Deze redenering leidt tot de volgende toestandslijn . De aard van de evenwichten is overigens ook via lokale linearisatie te bepalen: omdat $\varphi(y)=y^2+b\cdot y+1$ hebben we voor $\dfrac{\dd\varphi}{\dd y}$ in de evenwichten de waarden $\pm\sqrt{b^2-4}$, waarbij het minteken hoort bij de grootste waarde van de twee aanwezige evenwichten en het afstotende evenwicht aanduidt. Naarmate de waarde van $|b|$ dichter bij $2$ komt, komen de evenwichten ook dichter bij elkaar, in de buurt van $(2,-1)$ en $(-2,1)$ afhankelijk van het teken van de bifurcatieparameter $b$.

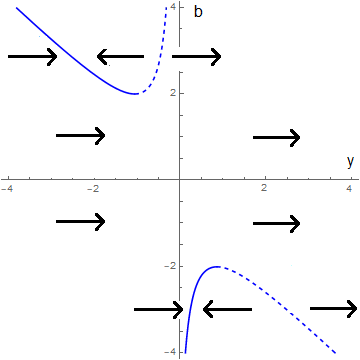
Een gebruikelijke manier om bifurcatie te illustreren is via het zogenaamde bifurcatiediagram. Hierin zijn de mogelijke evenwichten verticaal uitgezet tegen de parameter, die aanwezig is in de differentiaalvergelijking, op de horizontale as. Afstotende evenwichten liggen dan op lijnen die gestippeld getekend worden en aantrekkende evenwichten liggen op doorgetrokken lijnen om ze van elkaar te kunnen onderscheiden. In ons voorbeeld ziet het bifurcatiediagram er als volgt uit:

In onderstaande interactieve versie kun je de parameter $b$ variëren door de bijpassende groene driehoek over de horizontale as te verslepen. Zo kun je nagaan hoe het lijnelementenveld en het gedrag van oplossingskrommen afhangen van de bifurcatieparameter $b$. Door de afgeleide $y'$ als functie van $y$ te tonen kun je het teken van een evenwichtswaarde aflezen en zo de locatie van een evenwicht t.o.v. de oorsprong bepalen.