Saddle-node bifurcation

Ordinary differential equations: Bifurcations

Saddle-node bifurcation

We consider a simple one-dimensional dynamical system in which a bifurcation parameter is present, namely \[\frac{\dd y}{\dd t}=y^2+b\]

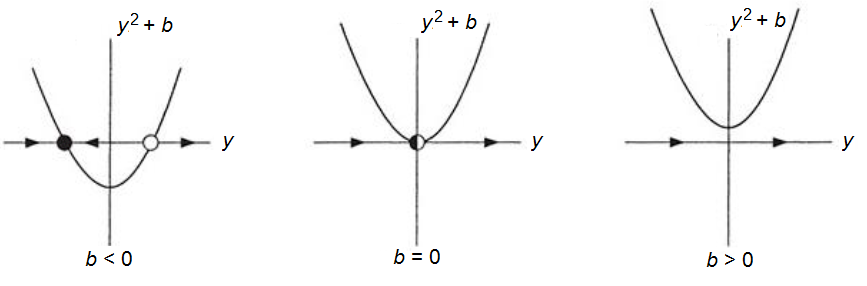
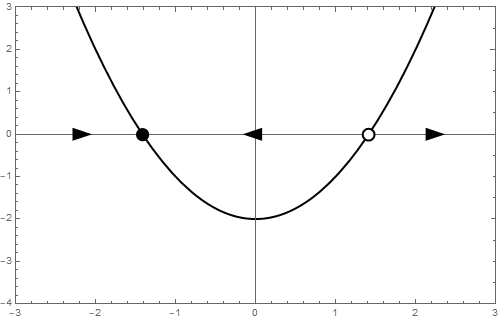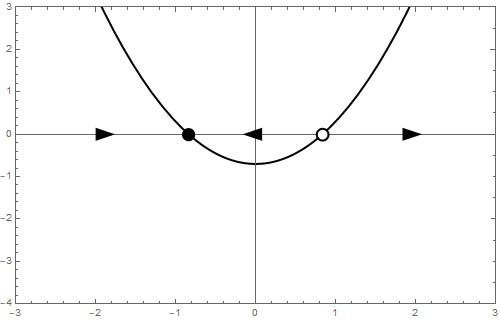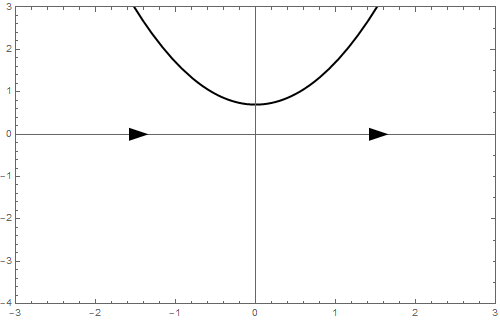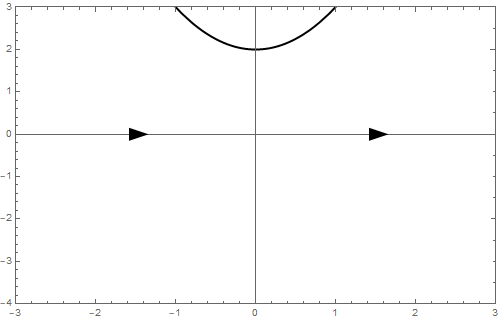
b = -1 We begin with a stability analysis of \[\frac{\dd y}{\dd t}=y^2-1\] This dynamical system can also be written as \[\frac{\dd y}{\dd t}=(y-1)(y+1)\] Now you can see immediately that there are two equilibria: \[y=-1\quad\text{and}\quad y=1\] The stability of these equilibria can be determined by local linearisation. If \[\varphi(y) = (y^2-1)\] then \[\frac{\dd \varphi}{\dd y}=2y\] and thus \[\frac{\dd \varphi}{\dd y}(-1)=-2\quad\text{and}\quad \frac{\dd \varphi}{\dd y}(1)=2 \] It follows that \(y=-1\) is an attractor and that \(y=1\) is a repeller. The phase line is as follows:

b = 0 If \[\frac{\dd y}{\dd t}=y^2\] then there exists only one equilibrium, namely \(y=0\). Because \(\varphi(y)\ge 0\) and is equal to \(0\) if \(y=0\), we have a so-called semi-stable equilibrium. This means here that for an initial value \(y_0<0\) the solution of the differential equation approaches the equilibrium, but that for an initial value \(y_0>0\) the solution curve of the differential equation moves away from the equilibrium. The phase line is as follows:

b = 1 We end with \[\frac{\dd y}{\dd t}=y^2+1\] In this case \(\varphi(y)>0\) and there does not exist any equilibrium; the phase line is as follows.

Saddle-node bifurcation In the previous three examples we have seen that the number of equilibria and their nature for the differential equation\[\frac{\dd y}{\dd t}=y^2+b\] depends on the values of \(b\). In general, the following is true:

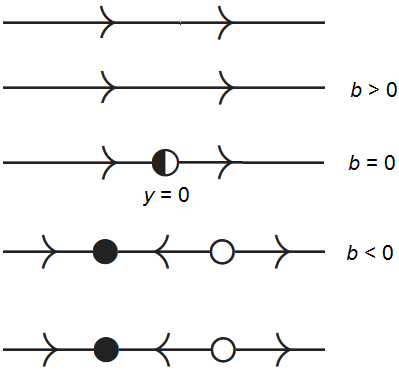
If \(b<0\) then there are two equilibria of which \(y=-\sqrt{|b|}\) is attracting and \(y=\sqrt{|b|}\) is repelling;
If \(b=0\) then a single semi-stable equilibrium exist;
If \(b>0\) then there is no equilibrium.

Three types of phase lines can be distinguished:

three types of phaseportraits

Qualitative changes in the number of equilibria and/or their nature are called bifurcations. The parameter values at which bifurcations occur are called bifurcation values or bifurcation points.

In this example, the number of the equilibria alters when the parameter value changes from negative to positive values. The following animation in a looping illustrates this.

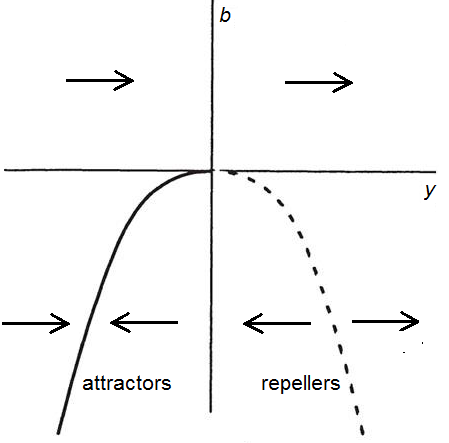
This kind of bifurcation, in which two equilibria get close together when the parameter approaches the bifurcation value and vanish at his point, is called a saddle-node bifurcation. The bifurcation diagram looks as follows:

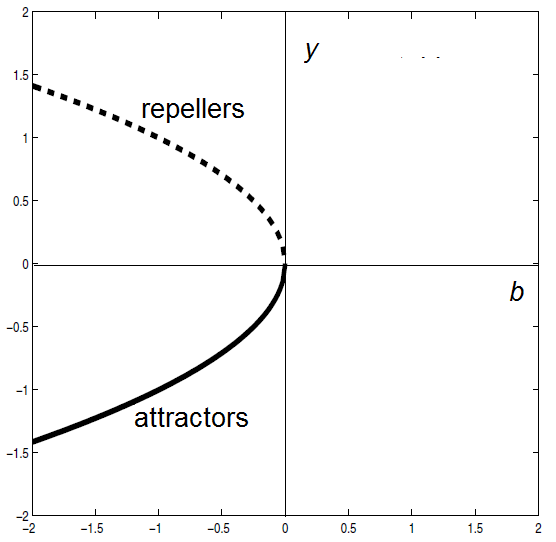
In the interactive version below you can vary the parameter \(b\) by dragging the corresponding green triangle along the horizontal axis. In this way you can explore how the slope field and the behaviour of solution curves depend on the bifurcation parameter \(b\). By displaying the derivative \(y'\) as a function of \(y\) you can read off the sign of an equilibrium value and thus determine the location of an equilibrium with respect to the origin.

\(\phantom{abc}\)

The bifurcation diagram can be understood and constructed as follows. For typical values of the parameter \(b\) we draw phase lines. In the picture below, the lines for the distinguished cases \(b<0\), \(b=0\) en \(b>0\) for the given ODE are shown.

phase portraits for distinguis parameter values

The vertical direction is used for the parameter \(b\) and the horizontal direction is used for \(y\); we have indicated the value \(y=0\) so that it is clear where equilibria are positioned. The figure reads in the upward direction as a series of phase lines for increasing parameter value. Joining nearby parameter values leads to dotted curves for repellers and solid curves for attractors, with the half-stable equilibrium marking the bifurcation. In this way, we get the following diagram in which the arrows indicate in which direction the solution curves would go in the course of time for the given parameter values:

However, the most common way to depict bifurcations it to invert the axes of the above figure, i.e., to mirror the diagram in the main diagonal of the coordinate system. Omitting the arrows, we get the following diagram, in which we have still indicated for clarity where attractors and repellers can be found (although the line style already indicates this):

Normal form of a saddle-node bifurcation In essence, there only two types of saddle-node bifurcations, associated with the so-called normal forms \[ \frac{\dd y}{\dd t}=b+ y^2\quad\text{and}\quad \frac{\dd y}{\dd t}=b-y^2\] The corresponding bifurcation diagrams are:

bifurcation diagrams of normal forms

In the stability analysis via local linearisation of the ODE \(\dfrac{\dd y}{\dd t}=\varphi(y)\) we look at the sign of the value of \(\varphi'(\eta)\) for an equilibrium \(\eta\) in order to decide whether it is stable or unstable. It is based on the property that solutions of the non-linear ODE \(\dfrac{\dd y}{\dd t}=\varphi(y)\) behave near the equilibrium as those of the linear differential equation \(\dfrac{\dd y}{\dd t}=\varphi'(\eta)(y-\eta)\), provided that \(\varphi'(\eta)\neq 0\). We keep parameter values fixed in this local linearisation, but bifurcations happen when for a certain parameter value \(\varphi'(\eta)= 0\).

In case of \(\varphi'(\eta)=0\), we still do something similar, but now we must take into account the bifurcation variable, say \(b\), as well and use the quadratic Taylor series approximation for functions of two variables. For an equilibrium \(\eta\) and a bifurcation value \(\beta\), we approximate the right-hand side of the ODE \(\dfrac{\dd y}{\dd t}=\varphi(y,b)\) in the neigbourhood of \(\eta\) and \(\beta\) in the following way: \[\varphi(y,b)\approx \varphi(\eta,\beta)+ (y-\eta)\cdot\frac{\partial \varphi}{\partial y}\!\Biggl|_{(\eta,\beta)} +(b-\beta)\cdot\frac{\partial \varphi}{\partial b}\!\Biggl|_{(\eta,\beta)} +\frac{1}{2}(y-\eta)^2\cdot \frac{\partial^2 \varphi}{\partial y^2}\!\Biggl|_{(\eta,\beta)}+ \ldots\] Because \(\varphi(\eta,\beta)=0\) (i.e., \(\eta\) is an equilibrium for bifurcation value \(\beta\)) and \(\frac{\partial \varphi}{\partial y}\!\Biggl|_{(\eta,\beta)}=0\) (this condition holds when \(\beta\) is a saddle-node bifurcation), we finally get \[\varphi(y,b)\approx (b-\beta)\cdot \frac{\partial \varphi}{\partial b}\!\Biggl|_{(\eta,\beta)} + \frac{1}{2}(y-\eta)^2 \cdot \frac{\partial^2 \varphi}{\partial y^2}\!\Biggl|_{(\eta,\beta)}\] The quadratic term that we have neglected in the Taylor series is \(\frac{1}{2} (b-\beta)^2\cdot \frac{\partial^2 \varphi}{\partial b^2}\!\Biggl|_{(\eta,\beta)}\), but this is anyway much smaller than the linear term \((b-\beta)\). We have also negelected the term \((y-\eta)(b-\beta)\cdot \frac{\partial^2 \varphi}{\partial y\partial b}\!\Biggl|_{(\eta,\beta)}\), but by completing the square of a quadratic polynomial we could have encorporated it anyway into the final quadratic term. So, in case \[ \frac{\partial \varphi}{\partial b}\!\Biggl|_{(\eta,\beta)}\neq 0\quad\text{and}\quad \frac{\partial^2 \varphi}{\partial y^2}\!\Biggl|_{(\eta,\beta)}\neq 0\] we have the differential equation \[\frac{\dd u}{\dd t}=p\cdot (b-\beta)+q\cdot u^2\] where \[u=y-\eta,\quad p = \frac{\partial\varphi}{\partial b}\!\Biggl|_{(\eta,\beta)},\quad q= \frac{1}{2}\cdot \frac{\partial^2 \varphi}{\partial y^2}\!\Biggl|_{(\eta,\beta)}\] When we define \(v=q\cdot u\) we have a differential equation of the form \[\frac{\dd v}{\dd t}=r+v^2\quad\text{or}\quad\frac{\dd v}{\dd t }=r-v^2\] for some parameter \(r\). These differential equations of \(v\) are called the normal forms of saddle-node bifurcations.

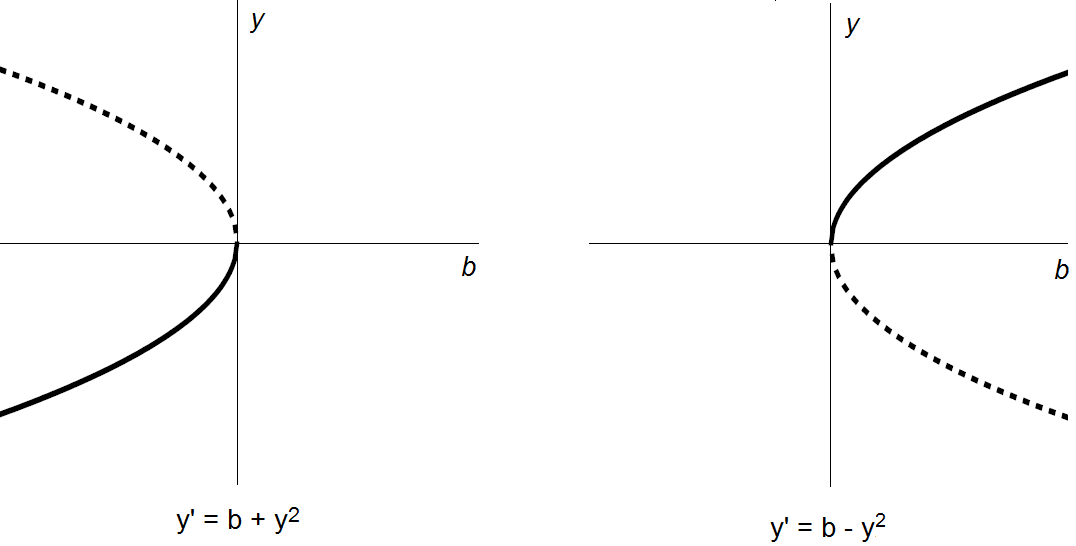
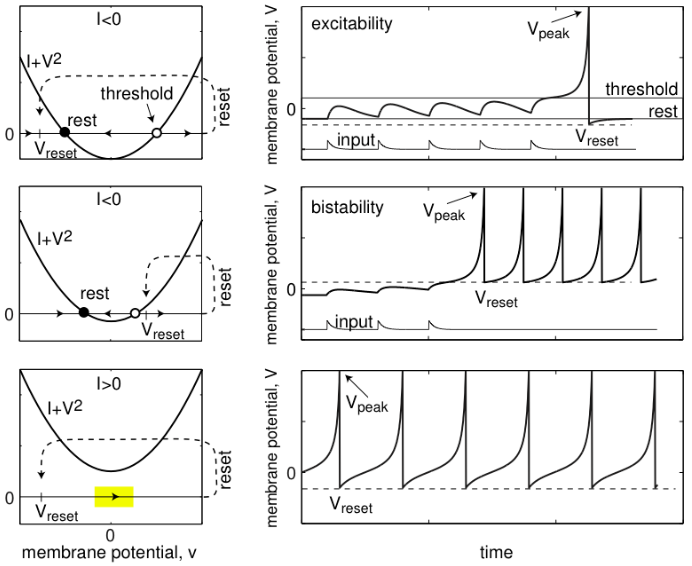
Generation of action potentials in a quadratic integrate-and-fire neuron As an application of saddle-node bifurcation we study the following mathematical model for a single neuron. In the so-called quadratic integrate-and-fire neuron, the dynamics of the membrane potential \(V\) of a neuron that is stimulated by a current \(I\) is described in nondimensional form by \[\frac{\dd V}{\dd t}=I+V^2\text{,}\quad \text{if } V\ge V_{\text{peak}}\text{, } V\leftarrow V_{\text{reset}}\] where \(V_{\text{peak}}\) is the peak (cut off) of a spike.

When \(I<0\), the right-hand side of the differential equation \(I+V^2\) has two roots, \(\pm\sqrt{|I|}\). The negative root corresponds with an attractor (the resting membrane potential \(V_{\text{rest}}\) of the neuron) and the positive root with a repeller (the firing threshold \(V_{\text{threshold}}\)). Depending on the reset value \(V_{\text{reset}}\) a single spike or periodic spiking will be generated once the membrane potential \(V\) passes for whatever reason the threshold value \(V_{\text{threshold}}\).

For \(V_{\text{reset}}<V_{\text{threshold}}\), a potential starting above the threshold value first increases to reach the maximum value \(V_{\text{peak}}\). Then it is reset in the basin of attraction of the stable equilibrium, which means that the voltage moves to the resting membrane potential \(V_{\text{rest}}\). So, one action potential is generated, after which the neuron goes back to the resting state. Note that the situation where \(V_{\text{reset}}<0\) is included in this case.

For \(V_{\text{reset}}>V_{\text{threshold}}\), the potential is reset in the basin of repelling to an infinite potential. The neuron exhibits periodic spiking because the reset value is also to the right of the unstable equilibrium. The firing frequency is bounded from below because the membrane potential is reset to the right of repeller and consequently the potential drop \(V_{\text{peak}}-V_{\text{reset}}\) has a maximum.

For \(I>0\), there are no equilibria and the neuron exhibits periodic spiking. In theory, the firing frequency can be arbitrary small because the sudden drop of the potential value \(V_{\text{peak}}-V_{\text{reset}}\) has no maximum.

The figure below, taken from the book Dynamical Systems in Neuroscience of Eugene M. Izhikevich (MIT Press, 2010, Figure 3.35, p. 81), shows the phase lines and potential-time profiles for the quadratic integrate-and-fire neuron model, as well as the behaviour of the neuron described above.

Izhikevich, figure 3.35

For \(I<0\) and \(V_{\text{reset}}>V_{\text{threshold}}\), in which case the neuron exhibits periodic spiking, the inter-spike interval can be computed as follows: \[\begin{aligned} T &=\int_{V_{\text{reset}}}^{V_{\text{peak}}}\frac{1}{V^2-|I|}\,\dd V\\ &=\left[\frac{1}{2\sqrt{|I|}}\ln\left(\frac{V-\sqrt{|I|}}{V+\sqrt{|I|}}\right)\right]_{V_{\text{reset}}}^{V_{\text{peak}}} \\ &= \frac{1}{2\sqrt{|I|}}\ln\left(\frac{\bigl(V_{\text{peak}}-\sqrt{|I|}\bigr)\bigl(V_{\text{reset}}+\sqrt{|I|}\bigr)}{\bigl(V_{\text{reset}}-\sqrt{|I|}\bigr)\bigl(V_{\text{peak}}+\sqrt{|I|}\bigr)}\right)\end{aligned}\] The firing frequency is equal to \(\dfrac{1}{T}\).

For \(I>0\), there are no equilibria and the neuron exhibits periodic spiking. The inter-spike interval can be computed, too: \[\begin{aligned} T &=\int_{V_{\text{reset}}}^{V_{\text{peak}}}\frac{1}{V^2+I}\,\dd V\\ &=\left[\frac{1}{\sqrt{I}}\arctan\left(\frac{V}{\sqrt{I}}\right)\right]_{V_{\text{reset}}}^{V_{\text{peak}}}\\ &= \frac{1}{\sqrt{I}}\arctan\left(\frac{V_{\text{peak}}}{\sqrt{I}}\right)-\frac{1}{\sqrt{I}}\arctan\left(\frac{V_{\text{reset}}}{\sqrt{I}}\right) \\ &=\frac{1}{\sqrt{I}}\arctan\left(\frac{\sqrt{I}\,(V_{\text{peak}}-V_{\text{reset}})}{I+V_{\text{peak}}\cdot V_{\text{reset}} }\right)\end{aligned}\] The firing frequency is equal to \(\dfrac{1}{T}\).