Gewone differentiaalvergelijkingen: Bifurcaties
Zadelknoopbifurcatie
We bekijken een eenvoudig 1-dimensionaal dynamisch systeem waarin een bifurcatieparameter voor komt, namelijk \[\frac{\dd y}{\dd t}=y^2+b\]
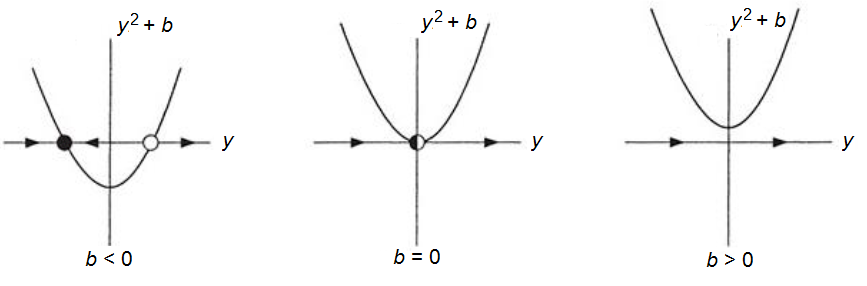
b = -1 We beginnen met een stabiliteitsonderzoek van \[\frac{\dd y}{\dd t}=y^2-1\] Dit dynamisch systeem is ook te schrijven als \[\frac{\dd y}{\dd t}=(y-1)(y+1)\] Hieraan zie je gelijk dat er twee evenwichten zijn: \[y=-1\quad\text{en}\quad y=1\] De stabiliteit van deze evenwichten kan door lokale linearisatie bepaald worden. Neem \[\varphi(y) = (y^2-1)\] Dan \[\frac{\dd\varphi}{\dd y}=2y\] en dus \[\frac{\dd \varphi}{\dd y}(-1)=-2\quad\text{en}\quad \frac{\dd \varphi}{\dd y}(1)=2 \] Hieruit volgt dat \(y=-1\) een aantrekkend evenwicht is en \(y=1\) een afstotend evenwicht is. De toestandslijn is als volgt:
b = 0 Als \[\frac{\dd y}{\dd t}=y^2\] dan is er nog maar één evenwicht, namelijk \(y=0\). Omdat \(\varphi(y)\ge 0\) en enkel gelijk aan \(0\) is als \(y=0\), hebben we een zogenaamd semistabiel evenwicht. Dit wil zeggen dat bij een startwaarde \(y_0<0\) de oplossing van de differentiaalvergelijking nadert naar het evenwicht, maar bij een startwaarde \(y_0>0\) de oplossing van de differentiaalvergelijking zich verwijdert van het evenwicht. In de toestandslijn geven we dit als volgt weer:
b = 1 We eindigen met \[\frac{\dd y}{\dd t}=y^2+1\] In dit geval is \(\varphi(y)>0\) en bestaat er helemaal geen evenwicht en ziet de toestandslijn er als volgt uit:
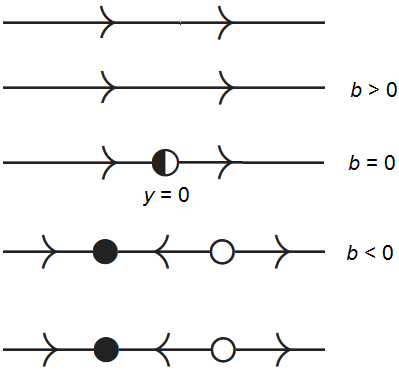
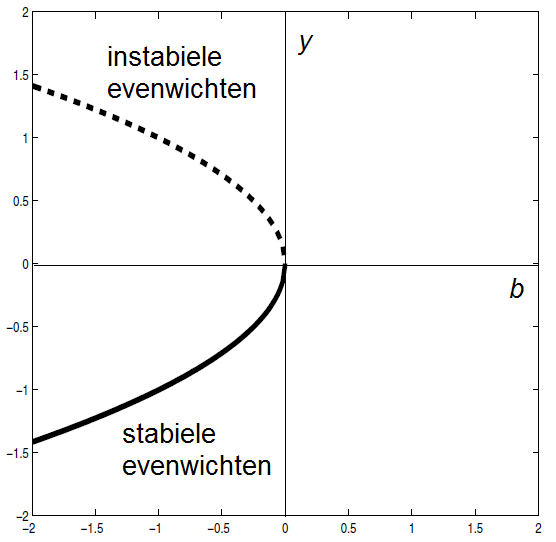
Zadelknoopbifurcatie We hebben in de vorige drie voorbeelden gezien dat het aantal evenwichten en hun aard bij de differentiaalvergelijking \[\frac{\dd y}{\dd t}=y^2+b\] afhangt van de waarden van \(b\). In het algemeen geldt:
- Als \(b<0\) dan zijn er twee evenwichten waarvan de ene, \(y=-\sqrt{|b|}\), aantrekkend is en de andere \(y=\sqrt{|b|}\) afstotend is;
- Als \(b=0\) dan is een één semistabiel evenwicht;
- Als \(b>0\) dan is er geen evenwicht.
We onderscheiden drie typen van toestandslijnen:
Kwalitatieve veranderingen in aantal evenwichten en/of hun aard heten bifurcaties. De parameterwaarden waarbij bifurcatie optreden heten bifurcatiewaarden of bifurcatiepunten. In dit voorbeeld verandert het aantal evenwichten wanneer de parameterwaarde wijzigt van negatief naar positief. Onderstaande animatie illustreert dit.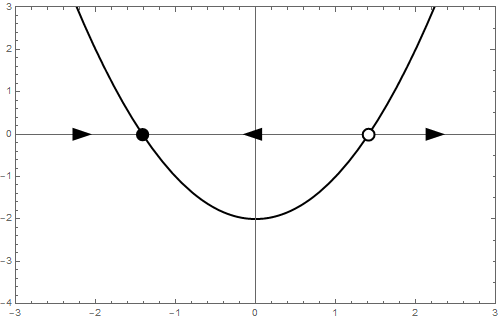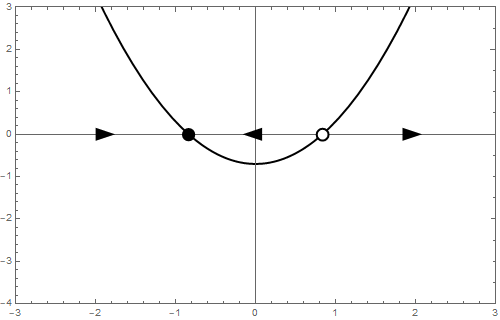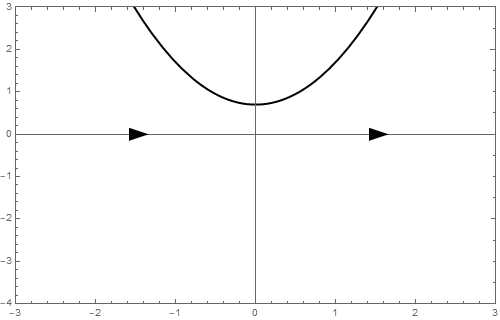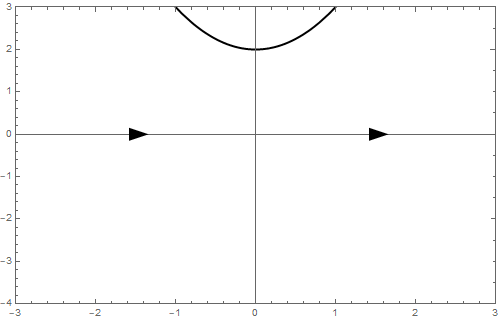
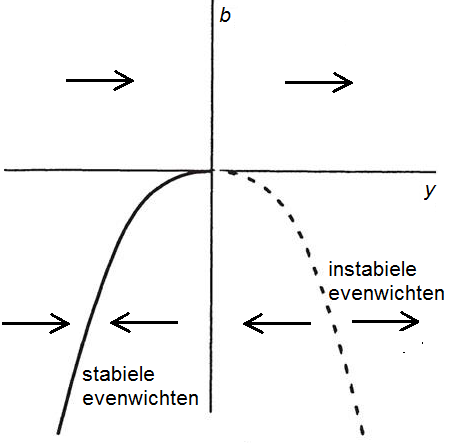
Dit type bifurcatie, waarbij twee evenwichten elkaar naderen als de parameter dichter bij de bifurcatiewaarde komt en verdwijnen bij deze parameterwaarde, wordt een zadelknoopbifurcatie genoemd. Het bifurcatiediagram ziet er als volgt uit:
In onderstaande interactieve versie kun je de parameter \(b\) variëren door de bijpassende groene driehoek over de horizontale as te verslepen. Zo kun je nagaan hoe het lijnelementenveld en het gedrag van oplossingskrommen afhangen van de bifurcatieparameter \(b\). Door de afgeleide \(y'\) als functie van \(y\) te tonen kun je het teken van een evenwichtswaarde aflezen en zo de locatie van een evenwicht t.o.v. de oorsprong bepalen.
\(\phantom{abc}\)Het bifurcatiediagram kan als volgt begrepen en geconstrueerd worden. Voor kenmerkende waarden van de parameter \(b\) tekenen we toestandslijnen. In onderstaande figuur hebben we toestandslijnen getekend voor de onderscheiden gevallen \(b<0\), \(b=0\) en \(b>0\) bij de gegeven GDV.
De verticale richting is gebruikt voor de parameter \(b\) en de horizontale richting voor \(y\); We hebben de waarden van \(y\) vermeld zodat het duidelijk is hoe evenwichten gepositioneerd zijn. Deze figuur leest van beneden naar boven als een serie van toestandslijnen bij opklimmende parameterwaarde. Door evenwichten bij nabijgelegen parameterwaarden te verbinden krijg je gestippelde krommen van afstotende evenwichten en doorgetrokken krommen van aantrekkende evenwichten, met de semistabiele evenwichten ter markering van bifurcatie. Op deze manier ontstaat onderstaande figuur waarin pijlen de richtingen van de oplossingskrommen bij gegeven parameterwaarden in de loop der tijd aangeven:
In de meest gebruikte manier om bifurcaties weer te geven worden de assen van bovenstaand diagram geïnverteerd, oftewel spiegel je de figuur langs de hoofddiagonaal van het assenstelsel. Wanneer we de pijlen weglaten, dan krijg je onderstaande figuur, waarin we voor de helderheid nog hebben aangeven waar aantrekkende en afstotende evenwichten zich bevinden (ook al geeft het gebruikte lijntype dit al aan):
Normaalvorm van een zadelknoopbifurcatie In essentie zijn er maar twee typen zadelknoopbifurcaties, passend bij de zogenaamde normaalvormen \[ \frac{\dd y}{\dd t}=b+ y^2\quad\text{en}\quad \frac{\dd y}{\dd t}=b-y^2\] De bijpassende bifurcatiediagrammen zijn:
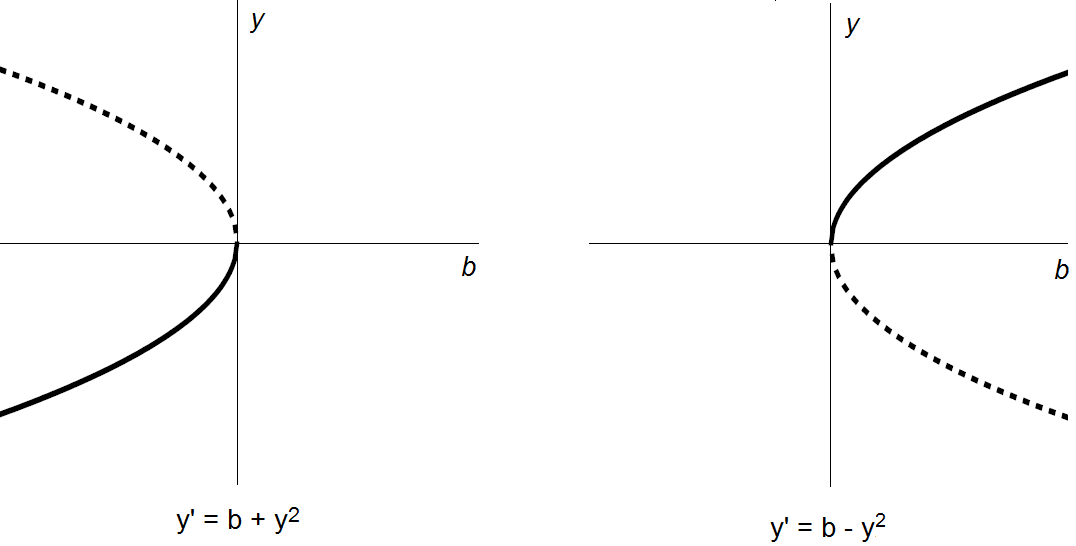
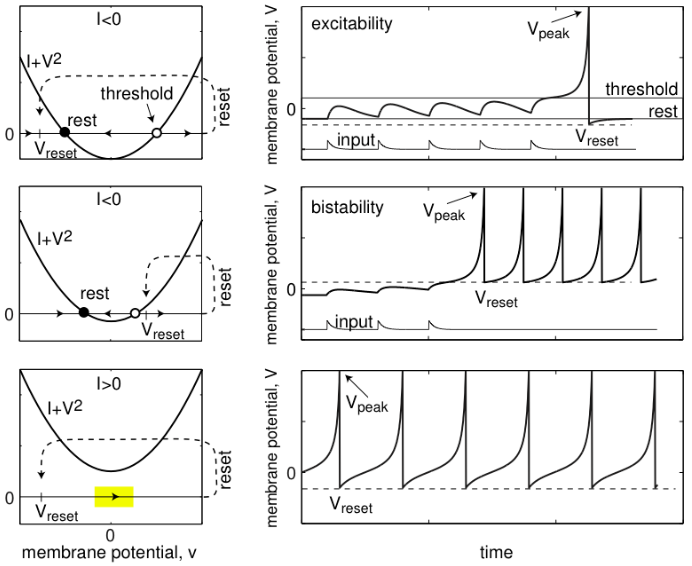
Actiepotentialen in een kwadratisch integrate-and-fire neuron Als toepassing van een zadelknoopbifurcatie bekijken we het volgende wiskundige model voor een enkel neuron. In het zogeheten kwadratische integrate-and-fire neuron wordt de dynamica van de membraanpotentiaal \(V\) van een neuron dat gestimuleerd wordt door een stroom \(I\) in dimensieloze wijze beschreven door \[\frac{\dd V}{\dd t}=I+V^2\text{,}\quad \text{als } V\ge V_{\text{peak}}\text{, } V\leftarrow V_{\text{reset}}\] waarbij \(V_{\text{peak}}\) de piekwaarde (afkapwaarde) van een actiepotentiaal is.
Als \(I<0\), dan heeft de rechterkant van de differentiaalvergelijking \(I+V^2\) twee wortels, \(\pm\sqrt{|I|}\). De negatieve wortel hoort bij een aantrekkend evenwicht (de rustmembraanpotentiaal \(V_{\text{rust}}\) van het neuron) en de positieve wortel mij een afstotend evenwicht (grenswaarde \(V_{\text{threshold}}\) voor het vuren van het neuron). Afhankelijk van de herstelwaarde \(V_{\text{reset}}\) treedt een enkele actiepotentiaal of periodiek vuren van het neuron op zodra de membraanpotentiaal \(V\) om wat voor reden de grenswaarde \(V_{\text{threshold}}\) passeert.
Als \(V_{\text{reset}}<V_{\text{threshold}}\) dan neemt een potentiaal boven de grenswaarde eerst toe totdat de piekwaarde \(V_{\text{peak}}\) bereikt wordt. Op dat moment wordt de potentiaal teruggezet naar een waarde die binnen het aantrekkingsgebied van het aantrekkende evenwicht ligt, hetgeen betekent dat de potentiaal richting de rustmembraanpotentiaal \(V_{\text{rest}}\) gaat. Er treedt dus één actiepotentiaal op waarna het neuron weer tot rust komt. Merk op dat dit het geval is in de situatie waarin \(V_{\text{reset}}<0\).
Als \(V_{\text{reset}}>V_{\text{threshold}}\) dan wordt de potentiaal teruggezet naar een waarde die rechts van het afstotende evenwicht ligt. De membraanpotentiaal zou oneindig groot worden, ware het niet dat deze bij het bereiken van een piekwaarde teruggezet wordt. Het neuron vuurt periodiek omdat herstelwaarde ook rechts van het afstotende evenwicht ligt. De vuurfrequentie is naar beneden begrensd omdat de membraanpotentiaal rechts van het afstotende evenwicht ligt en de potentiaalvermindering \(V_{\text{peak}}-V_{\text{reset}}\) een maximale waarde heeft.
Als \(I>0\) dan zijn er geen evenwichten en vuurt het neuron periodiek. In theorie kan de vuurfrequentie willekeurig klein worden omdat de potentiaalvermindering \(V_{\text{peak}}-V_{\text{reset}}\) onbegrensd is.
Onderstaande figuur, overgenomen uit het boek Dynamical Systems in Neuroscience van Eugene M. Izhikevich (MIT Press, 2010, Figure 3.35, p. 81), toont de toestandslijnen en de potentiaal-tijd grafieken voor het kwadratische integrate-and-fire neuron model samen met het gedrag van het neuron dat we hierboven hebben beschreven.
