b = -1 We begin with a stability analysis of \[\frac{\dd y}{\dd t}=-y-y^2\] This dynamical system can also be written as \[\frac{\dd y}{\dd t}=-y\,(y+1)\] Now you can see immediately that there are two equilibria: \[y=-1\quad\text{and}\quad y=0\] The stability of these equilibria can be determined by local linearization. If \[\varphi(y) = -y-y^2\] then \[\frac{\dd \varphi}{\dd y}=-1-2y\] and thus \[\frac{\dd \varphi}{\dd y}(-1)=1\quad\text{and}\quad \frac{\dd \varphi}{\dd y}(0)=-1 \] It follows that \(y=-1\) is a repeller and that \(y=0\) is an attractor. The phase line is as follows:

b= 0 If \[\frac{\dd y}{\dd t}=-y^2\] then there exists only one equilibrium, namely \(y=0\). Because \(\varphi(y)\le 0\) is equal to \(0\) if and only if \(y=0\), we have a so-called semi-stable equilibrium. This means here that for an initial value \(y_0>0\) the solution of the differential equation approaches the equilibrium, but that for an initial value \(y_0<0\) the solution curve of the differential equation moves away from the equilibrium. The phase line is as follows:

b = 1 We end with \[\frac{\dd y}{\dd t}=y-y^2\] This dynamical system can also be written as \[\frac{\dd y}{\dd t}=-y\,(1-y)\] Now you can see immediately that there are two equilibria: \[y=0\quad\text{and}\quad y=1\] The stability of these equilibria can be determined by local linearization. If \[\varphi(y) = y-y^2\] then \[\frac{\dd \varphi}{\dd y}=1-2y\] and thus \[\frac{\dd \varphi}{\dd y}(0)=1\quad\text{and}\quad \frac{\dd \varphi}{\dd y}(1)=-1 \] It follows that \(y=0\) is a repeller and that \(y=1\) is an attractor. The phase line is as follows:

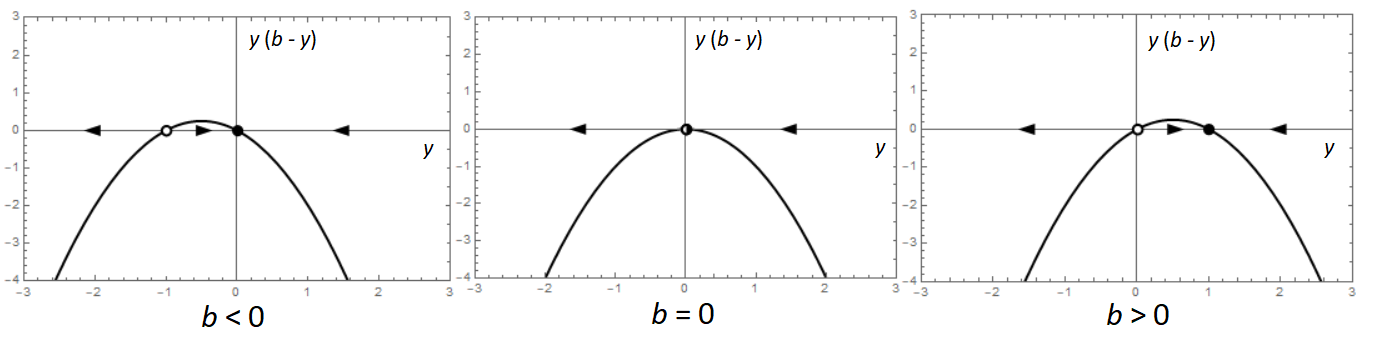
Transcritical bifurcation In the previous three examples we have seen that the number of equilibria and their nature for the differential equation \[\frac{\dd y}{\dd t}=b\cdot y-y^2\] depends on the values of \(b\). In general, the following is true:

• if \(b<0\) then there are two equilibria of which \(y=0\) is attracting and \(y=b\) is repelling;
• if \(b=0\) then a single semi-stable equilibrium exist;
• if \(b>0\) then there are two equilibria of which \(y=0\) is repelling and \(y=b\) is attracting.

Three types of phase lines can be distinguished:

The types of the equilibria changes from negative to positive parameter value. The following animation in a looping illustrates the change in the phase line when the bifurcation parameters moves from negative values to positive values.

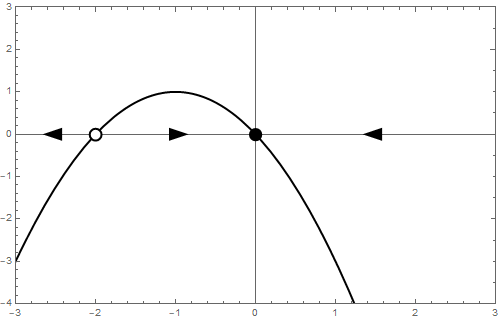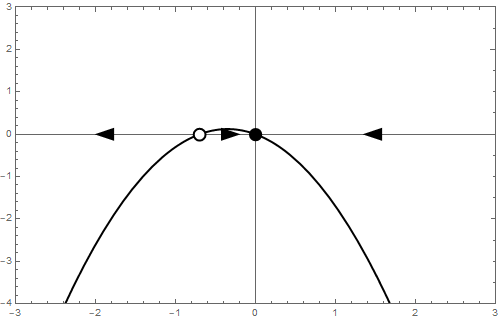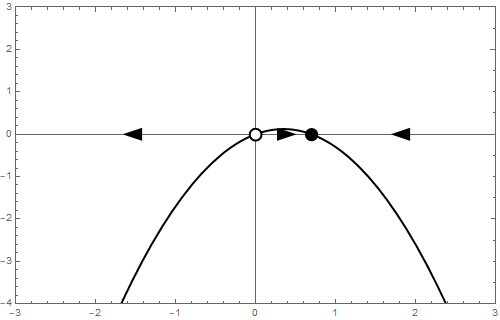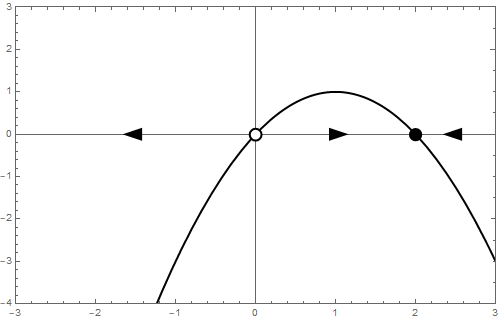
The bifurcation diagram looks as follows:

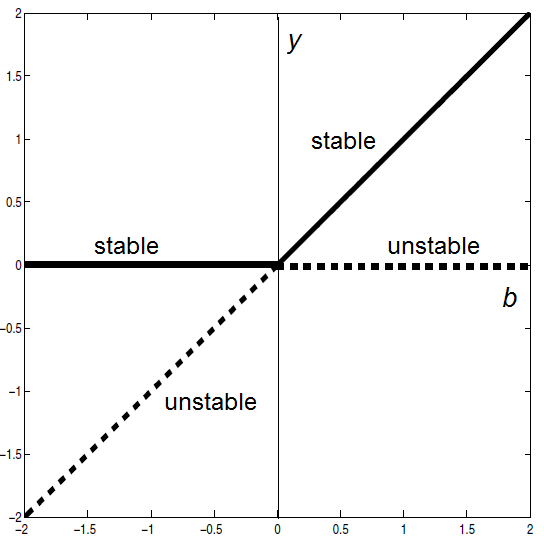
This kind of bifurcation, in which two equilibria get close together when the parameter approaches the bifurcation value and exchange stability at his point, is called a transcritical bifurcation.

In the interactive version below you can vary the parameter \(b\) by dragging the corresponding green triangle along the horizontal axis. In this way you can explore how the slope field and the behaviour of solution curves depend on the bifurcation parameter \(b\). By displaying the derivative \(y'\) as a function of \(y\) you can read off the sign of an equilibrium value and thus determine the location of an equilibrium with respect to the origin.