b = -1 We beginnen met \[\frac{\dd y}{\dd t}=-y-y^2\] Dit dynamisch systeem is ook te schrijven als \[\frac{\dd y}{\dd t}=-y\,(y+1)\] Hieraan zie je gelijk dat er twee evenwichten zijn: \[y=-1\quad\text{en}\quad y=0\] De stabiliteit van deze evenwichten kunnen door lokale linearisatie bepalen. Neem \[\varphi(y) = -y-y^2\] Dan \[\frac{\dd \varphi}{\dd y}=-1-2y\] en dus \[\frac{\dd \varphi}{\dd y}(-1)=1\quad\text{en}\quad \frac{\dd \varphi}{\dd y}(0)=-1 \] Hieruit volgt dat \(y=-1\) een afstotend evenwicht is en \(y=0\) een aantrekkend evenwicht is. De toestandslijn is als volgt:

b= 0 Als \[\frac{\dd y}{\dd t}=-y^2\] dan is er nog maar één evenwicht, namelijk \(y=0\). Omdat \(\varphi(y)\le 0\) en enkel gelijk aan \(0\) is als \(y=0\), hebben we een zogenaamd semistabiel evenwicht. Dit wil zeggen dat bij een startwaarde \(y_0>0\) de oplossing van de differentiaalvergelijking nadert naar het evenwicht, maar bij een startwaarde \(y_0<0\) de oplossing van de differentiaalvergelijking zich verwijdert van het evenwicht. In de toestandslijn geven we dit als volgt weer:

b = 1 We eindigen met \[\frac{\dd y}{\dd t}=y-y^2\] Dit dynamisch systeem is ook te schrijven als \[\frac{\dd y}{\dd t}=-y\,(1-y)\] Hieraan zie je gelijk dat er twee evenwichten zijn: \[y=0\quad\text{en}\quad y=1\] De stabiliteit van deze evenwichten kunnen door lokale linearisatie bepalen. Neem \[\varphi(y) = y-y^2\] Dan \[\frac{\dd \varphi}{\dd y}=1-2y\] en dus \[\frac{\dd \varphi}{\dd y}(0)=1\quad\text{en}\quad \frac{\dd \varphi}{\dd y}(1)=-1 \] Hieruit volgt dat \(y=0\) een afstotend evenwicht is en \(y=1\) een aantrekkend evenwicht is. De toestandslijn is als volgt:

Transkritische bifurcatie We hebben in de vorige drie voorbeelden dat het aantal evenwichten en hun aard bij de differentiaalvergelijking \[\frac{\dd y}{\dd t}=b\cdot y-y^2\] afhangt van de waarden van \(r\). In het algemeen geldt:

• Als \(b<0\) dan zijn er twee evenwichten waarvan de ene, \(y=0\), aantrekkend is en de andere \(y=b\) afstotend is;
• Als \(b=0\) dan is er één semistabiel evenwicht;
• Als \(b>0\) dan zijn er twee evenwichten waarvan de ene, \(y=0\), afstotend is en de andere \(y=b\) aantrekkend is.

We kunnen drie typen toestandslijnen onderscheiden:

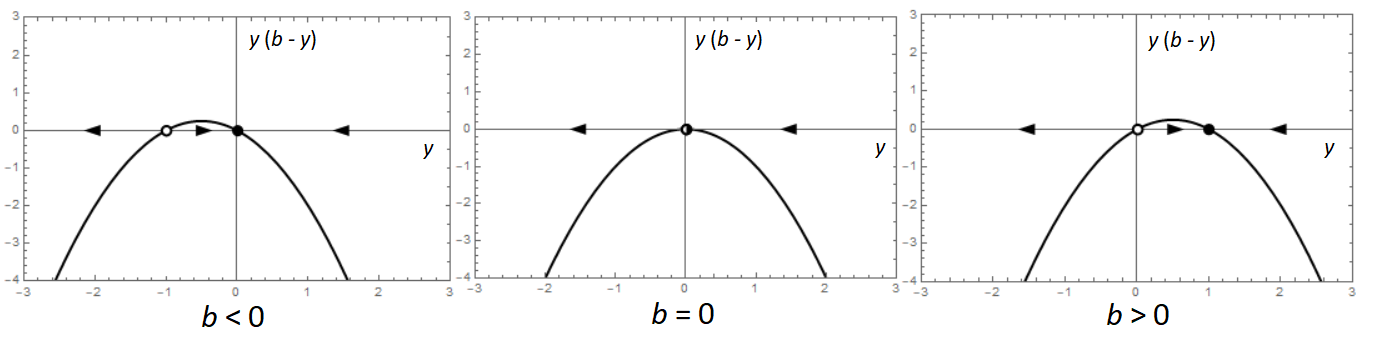
De aard van de twee evenwichten verandert van negatieve naar positieve parameterwaarde. Onderstaande animatie toont de verandering in de toestandslijn wanneer de bifurcatieparameter van negatieve naar positieve waarden gaat.

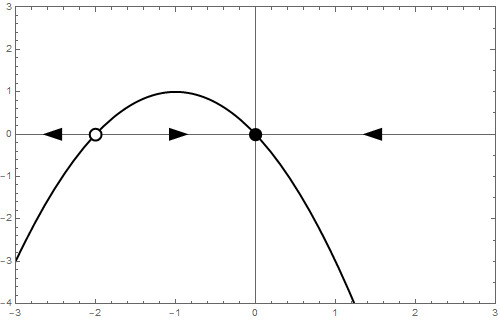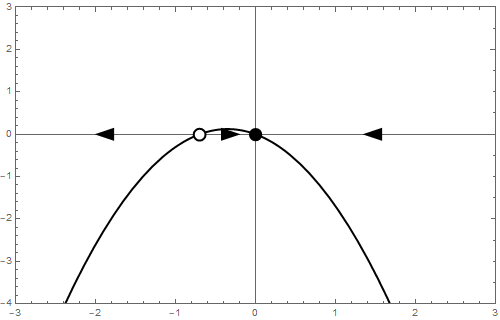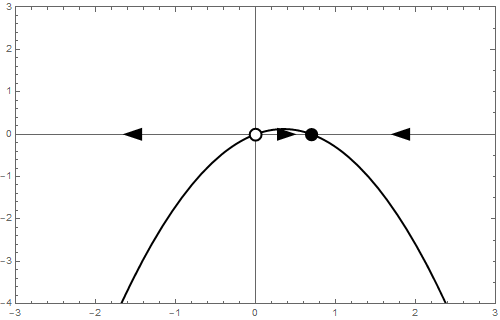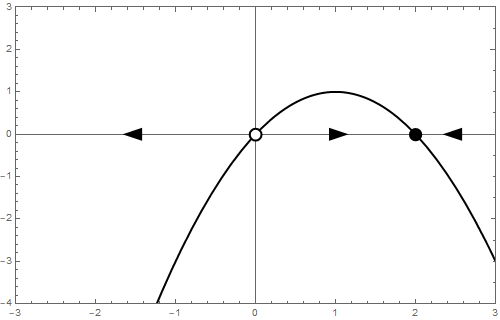
Het bifurcatiediagram ziet er als volgt uit:

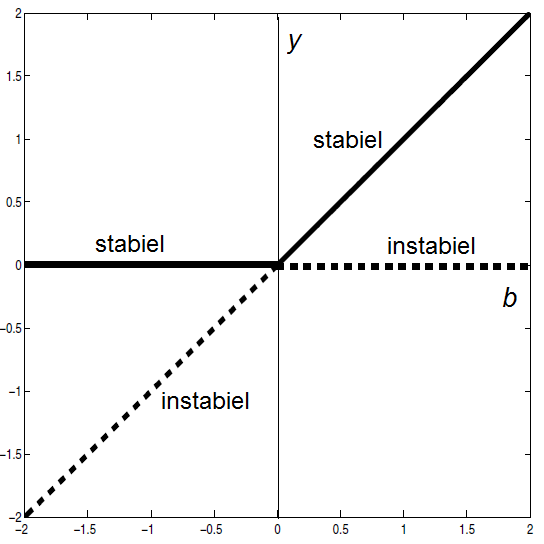
Dit type bifurcatie, waarin twee evenwichten bij elkaar komen als de parameter de bifurcatiewaarde nadert en de stabiliteit in dit punt uitwisselen, heeft een transkritsche bifurcatie.

In onderstaande interactieve versie kun je de parameter \(b\) variëren door de bijpassende groene driehoek over de horizontale as te verslepen. Zo kun je nagaan hoe het vectorveld en het gedrag van oplossingskrommen afhangen van de bifurcatieparameter \(b\). Door de afgeleide \(y'\) als functie van \(y\) te tonen kun je het teken van een evenwichtswaarde aflezen en zo de locatie van een evenwicht t.o.v. de oorsprong bepalen.