Ordinary differential equations: Bifurcations
 Pitchfork bifurcation
Pitchfork bifurcation
We consider a simple one-dimensional dynamical system in which a bifurcation parameter is present, namely \[\frac{\dd y}{\dd t}=b\cdot y-y^3\]
b = -1 We begin with a stability analysis of \[\frac{\dd y}{\dd t}=-y-y^3\] This dynamical system can also be written as \[\frac{\dd y}{\dd t}=-y\,(y^2+1)\] The only one equilibrium is \(y=0\). The stability of this equilibrium can be determined by local linearization. If \[\varphi(y) = -y-y^3\] then \[\frac{\dd \varphi}{\dd y}=-1-3y^2\] and thus \[\frac{\dd \varphi}{\dd y}(0)=-1\] Consequently, \(y=0\) is an attractor and the phase line is as follows:
![]()
b = 0 If \[\frac{\dd y}{\dd t}=-y^3\] then there is still only one equilibrium, namely \(y=0\). If \(y<0\) then \(\varphi(y)>0\), and if \(y<0\), then \(\varphi(y)<0\). Consequently, \(y=0\) is an attractor and the phase line is as follows:
![]()
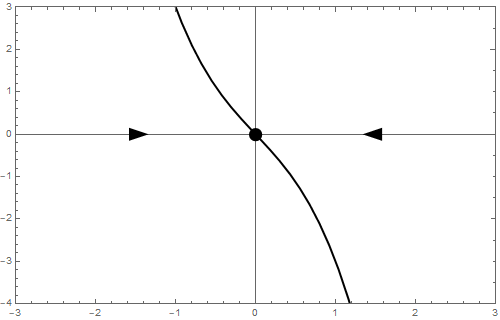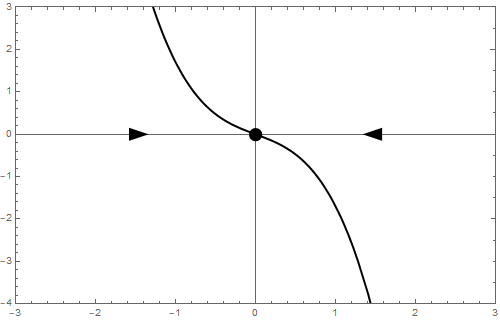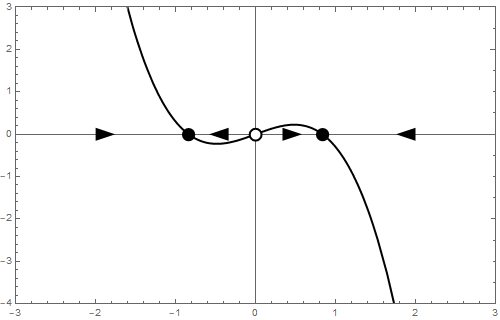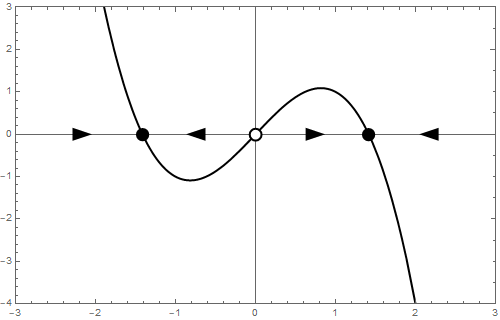
b = 1 We end with \[\frac{\dd y}{\dd t}=y-y^3\] This dynamic system can also be written as \[\frac{\dd y}{\dd t}=y\,(1-y)\,(1+y)\] Now you can see immediately that there are three equilibria:\[y=-1,\quad y=0\quad\text{and}\quad y=1\] The stability of these equilibria can be determined by local linearization. If \[\varphi(y) = y-y^3\] then \[\frac{\dd \varphi}{\dd y}=1-3y^2\] and thus \[\frac{\dd \varphi}{\dd y}(-1)=-2\qquad\frac{\dd \varphi}{\dd y}(0)=1\qquad\text{and}\qquad \frac{\dd \varphi}{\dd y}(1)=-2 \] Consequently \(y=-1\) and \(y=1\) are attractors and \(y=0\) is a repeller. The phase line is as follows:
![]()
Supercritical pitchfork bifurcation In the previous three examples we have seen that the number of equilibria and their nature for the differential equation \[\frac{\dd y}{\dd t}=b\cdot y-y^3\] depends on the values of \(b\). In general, the following is true:
- If \(b\le 0\) then one equilibrium exist, namely \(y=0\), and it is an attractor;
- If \(b>0\) there are three equilibria, one of which, namely \(y=0\), is repelling and the other two equilibria, \(y=-\sqrt{b}\) and \(y=\sqrt{b}\), are attracting.
Three types of phase lines can be distinguished:
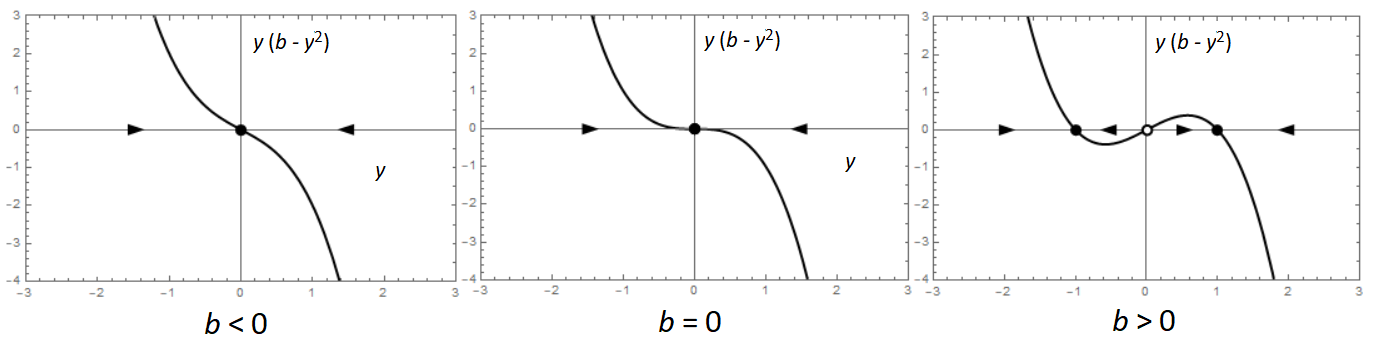
The number of equilibria changes from negative to positive parameter value. The following animation in a looping illustrates the change in the phase line when the bifurcation parameters moves from negative values to positive values.
The bifurcation diagram looks as follows:
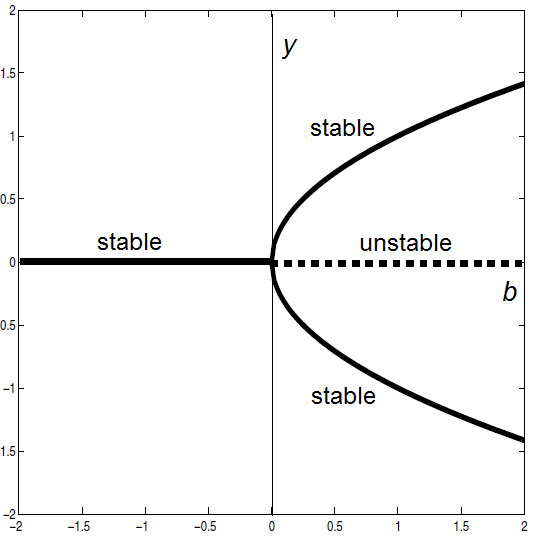
This kind of bifurcation, in which new stable equilibria appear when the parameter crosses the bifurcation value, is called a supercritical pitchfork bifurcation.
In the interactive version below you can vary the parameter \(b\) by dragging the corresponding green triangle along the horizontal axis. In this way you can explore how the slope field and the behaviour of solution curves depend on the bifurcation parameter \(b\). By displaying the derivative \(y'\) as a function of \(y\) you can read off the sign of an equilibrium value and thus determine the location of an equilibrium with respect to the origin.
Subcritical pitchfork bifurcation A subcritical pitchfork bifurcation, in which unstable equilibria disappear when the parameter crosses the bifurcation value, also exists; for instance, for the differential equation \[\frac{\dd y}{\dd t}=b\cdot y+y^3\] For this ODE, the following is true:
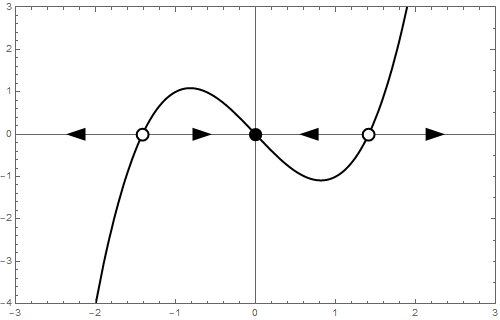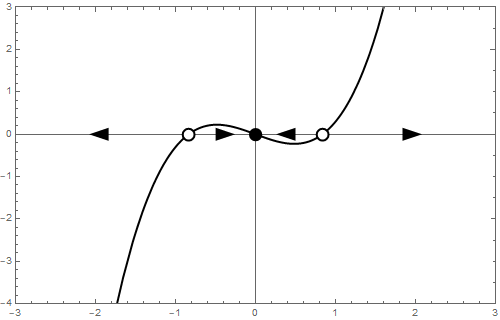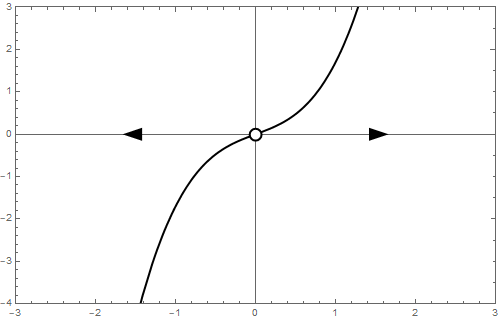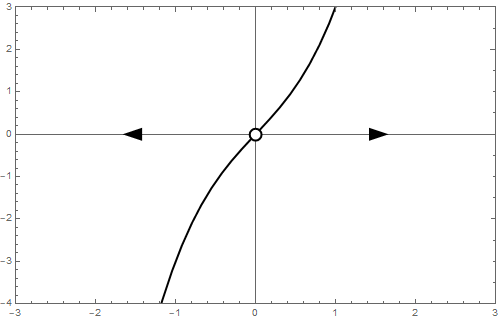
- if \(b<0\) there are three equilibria, one of which, namely \(y=0\), is attracting and the other two equilibria, \(y=-\sqrt{|b|}\) and \(y=\sqrt{|b|}\), are repelling;
- if \(b=0\) then one equilibrium exist, namely \(y=0\), and it is a repeller.
Three types of phase lines can be distinguished:
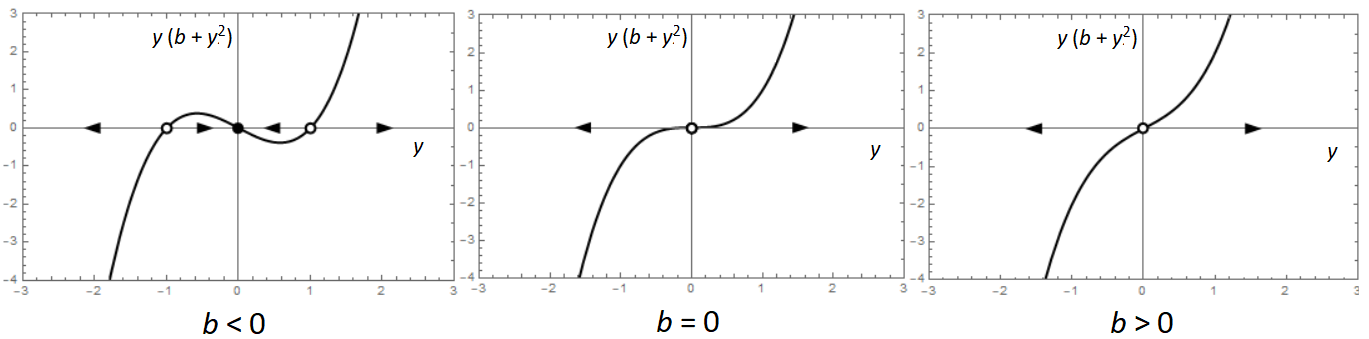
The number of equilibria changes from negative to positive parameter value. The following animation in a looping illustrates the change in the phase line when the bifurcation parameters moves from negative values to positive values.
The bifurcation diagram looks as follows:
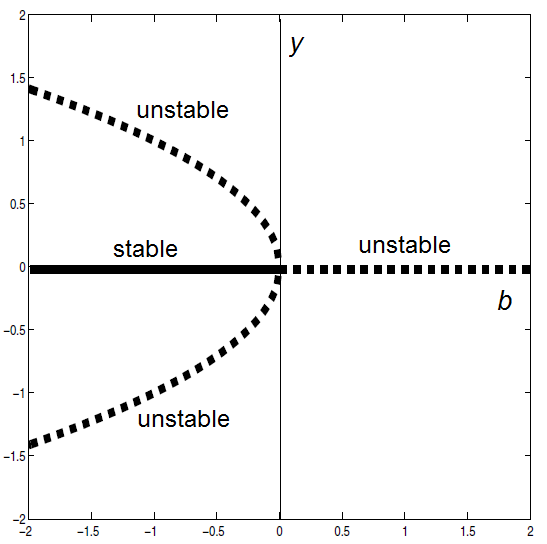
Naming The above explanation about supercritical and subcritical bifurcation was a bit sloppy. Better are the following definitions. Let the bifurcation parameter change in the direction leading to an increase in the number of objects (equilibria and, as we will encounter later, limit cycles). The bifurcation is supercritical if stable object appear, subcritical if unstable objects appear, and transcritical if equal numbers of stable and unstable objects appear or disappear.


