Uitwerking We definiëren $$\varphi(y)=y^2+y+b$$ Om de evenwichten van de differentiaalvergelijking te vinden moeten we de vergelijking $\varphi(y)=0$ oplossen. Dit is met de $abc$-formule te doen: $$y=\frac{-1\pm\sqrt{1-4b}}{2}$$ waarbij er alleen reële oplossingen zijn als $1-4b\ge 0$ oftewel als $b\le \tfrac{1}{4}$.

Om de aard van de evenwichten te achterhalen gebruiken we lokale linearisatie. Omdat $\varphi'(y)=2y+1$ vinden we in de evenwichten de waarden $\pm\sqrt{1-4b}$. Hieruit volgt, onder de voorwaarde $b< \tfrac{1}{4}$, dat er twee evenwichten zijn waarbij $y=-\tfrac{1}{2} - \tfrac{1}{2}\sqrt{1-4b}$ een aantrekkend evenwicht is en $y=-\tfrac{1}{2} + \tfrac{1}{2}\sqrt{1-4b}$ een afstotend evenwicht is. De toestandslijn ziet er onder deze voorwaarden als volgt uit:

Dit resultaat is in overeenstemming met het gegeven dat $\varphi(y)$ een dalparabool is en je via het tekenverloop van $\varphi(y)$ tot dezelfde conclusie komt. Als $b= \tfrac{1}{4}$, dan hebben we alleen maar een semistabiel evenwicht en is de toestandslijn als volgt:

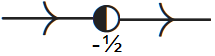
Als $b>\tfrac{1}{4}$, dan zijn er geen evenwichten en is de toestandslijn gelijk aan

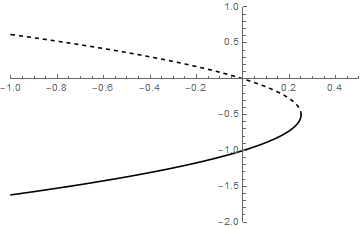
Er is hier sprake van een zadelknoopbifurcatie en het bifurcatiediagram ziet er als volgt uit:

Uitwerking We definiëren $$\varphi(y)=b\cdot y^2+y+1$$ Om de evenwichten van de differentiaalvergelijking te vinden moeten we de vergelijking $\varphi(y)=0$ oplossen. Dit is met de $abc$-formule te doen: $$y=\frac{-1\pm\sqrt{1-4b}}{2b}$$ waarbij er alleen reële oplossingen zijn als $1-4b\ge 0$ oftewel als $b\le \tfrac{1}{4}$ en het geval $b=0$ apart behandeld wordt met als evenwicht $y=-1$.

Om de aard van de evenwichten te achterhalen gebruiken we lokale linearisatie. Omdat $\varphi'(y)=2b\cdot y+1$ vinden we in de evenwichten de waarden $\pm\sqrt{1-4b}$. Hieruit volgt dat er twee evenwichten zijn waarbij $y=-\tfrac{1}{2b} - \tfrac{1}{2b}\sqrt{1-4b}$ een aantrekkend evenwicht is en $y=-\tfrac{1}{2b} + \tfrac{1}{2b}\sqrt{1-4b}$ een afstotend evenwicht is. De toestandslijn, waarbij we de ligging van de evenwichten aanduiden, ziet er onder voorwaarde $0<b< \tfrac{1}{4}$ als volgt uit:

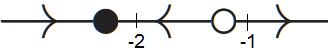
Als $b<0$ dan ziet de toestandslijn er als volgt uit:

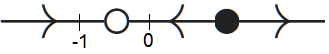
Dit resultaat is in overeenstemming met het gegeven dat $\varphi(y)$ een dalparabool is als $b>0$ en een bergparabool is als $b<0$, en je via het tekenverloop van $\varphi(y)$ tot dezelfde conclusie komt.

Als $b=0$ hebben we één evenwicht, namelijk $y=-1$, en dat is afstotend omdat dan $\varphi'(-1)=1>0$. De toestandslijn is dan

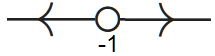
Als $b= \tfrac{1}{4}$, dan is $\varphi(y)$ te schrijven als $(\tfrac{1}{2}y+1)^2$ en hebben we alleen maar een semistabiel evenwicht, namelijk $y=-2$, en is de toestandslijn als volgt:

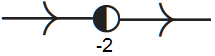
Als $b>\tfrac{1}{4}$, dan zijn er geen evenwichten en is de toestandslijn gelijk aan

Bij $b=\tfrac{1}{4}$ gaat het om een zadelknoopbifurcatie (het aantal evenwichten wijzigt van 2 naar 0).

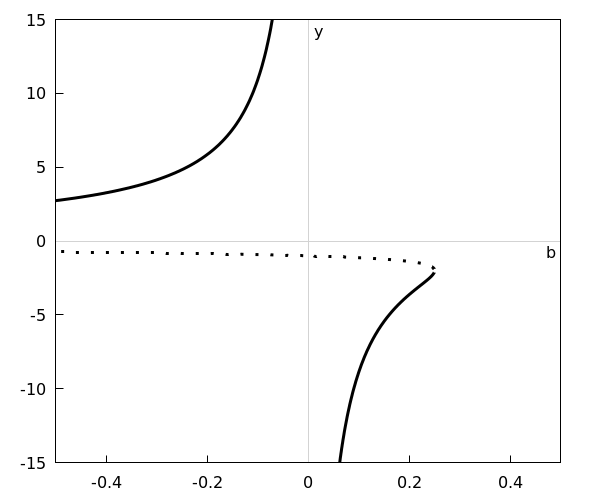
Om het bifurcatiediagram te tekenen moet je precies uitzoeken waar de nulpunten van $\varphi(y)$ zich bij verschillende waarden van de parameter $b$ zich bevinden. Een op de computer gegenereerd bifurcatiediagram ziet er als volgt uit:

Uitwerking We definiëren $$\varphi(y)=b\cdot y^3+y$$ Om de evenwichten van de differentiaalvergelijking te vinden moeten we de vergelijking $\varphi(y)=0$ oplossen. Dit gaat het gemakkelijkst als je $\varphi(y)$ herschrijft als $y\,(b\cdot y^2 +1)$. Dan zie je dat $y=0$ een evenwicht is en dat de andere evenwichten van de parameter $b$ afhangen omdat daarvoor moet gelden dat $b\cdot y^2 + 1=0$. Als $b=0$, zijn er geen verdere evenwichten. Ook als $b>0$ dan zijn er ook geen verdere evenwichten omdat $b\cdot y^2 + 1$ dan een dalparabool is met minimumwaarde gelijk aan $1$. Als $b<0$ dan is $b\cdot y^2 + 1$ een bergparabool met nulpunten $y={\pm}1\bigl/\sqrt{|b|}$.

Om de aard van de evenwichten te achterhalen gebruiken we lokale linearisatie. Omdat $\varphi'(y)=3b\cdot y^2+1$ hebben we $\varphi'(0)=1$ en is het evenwicht $y=0$ afstotend. Ook hebben we $\varphi'\Bigl({\pm}1\bigl/\sqrt{|b|}\Bigr)=-2$ en zijn de twee evenwichten $y={\pm}1\bigl/\sqrt{|b|}$ dus aantrekkend.

Uit het bovenstaande volgt dat we maar twee soorten toestandslijnen hoeven te onderscheiden:

Als $b\ge 0$ dan

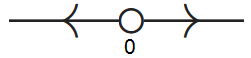
Als $b<0$ dan

en de aantrekkende evenwichten verschuiven naar buiten toe bij opklimmende waarden van $b$ en liggen dichter bij elkaar voor naarmate $b$ meer negatief is.

Het bifurcatiediagram ziet er als volgt uit:

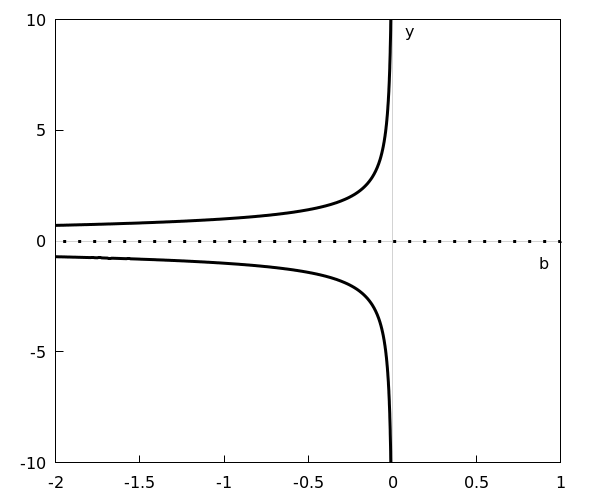
De bifurcatie $b=0$ is een superkritische bifurcatie want als de bifurcatieparameter van positieve naar negatieve waarden wijzigt neemt het aantal stabiele evenwichten toe.

Uitwerking We definiëren $$\varphi(y)=y\cdot \left(1-\frac{y}{4}\right)-b$$ Om de evenwichten van de differentiaalvergelijking te vinden moeten we de vergelijking $\varphi(y)=0$ oplossen. Aan de vorm van de functie $\varphi(y)$ lezen we af dat het hier om een bergparabool $y\cdot \left(1-\frac{y}{4}\right)$ gaat die verschoven is in verticale richting met $-b$. Als we de haakjes in de veelterm wegwerken krijgen we $$\varphi(y)= -\tfrac{1}{4}y^2+y-b$$ en de $abc$-formule geeft als nulpunten $$y=\frac{-1\pm\sqrt{1-b}}{-\tfrac{1}{2}}=2\pm2\sqrt{1-b}$$ mits $b\ge 1$. Er zijn dus alleen evenwichten als $b\ge 1$.

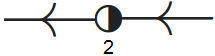
In het geval $b=1$ geldt dat $\varphi(y)=-(\tfrac{1}{2}y-1)^2$ zodat uit het tekenverloop van $\varphi(y)$ volgt dat we nu te maken hebben met een semistabiel evenwicht $y=2$ en toestandslijn van de vorm

Als $b<1$ dan zijn er twee evenwichten $y=2\pm 2\sqrt{1-b}$ en omdat $\varphi(y)$ een bergparabool is volgt uit het tekenverloop van $\varphi(y)$ dat $y=2-2\sqrt{1-b}$ een afstotend evenwicht is, $y=2+2\sqrt{1-b}$ een aantrekkend evenwicht is, en dat de toestandslijn er uit ziet als

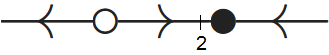
Het bifurcatiediagram ziet er als volgt uit:

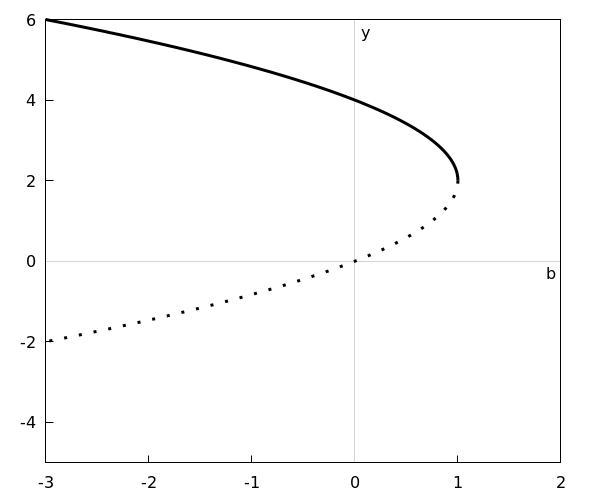
Het betreft hier een zadelknoopbifurcatie.

Uitwerking We definiëren $$\varphi(y)=b\cdot y-\frac{y}{1+y}$$ Om de evenwichten van de differentiaalvergelijking te vinden moeten we de vergelijking $\varphi(y)=0$ oplossen.

Als $b=0$ dan $$\varphi(y)=-\frac{y}{1+y}$$ en is er één evenwicht $y=0$. In de buurt hiervan is het tekenverloop van $\varphi(y)$ gelijk aan het tekenverloop van $-y$ en daarom is $y=0$ een aantrekkend evenwicht.

Als $b\neq 0$ dan $$\begin{aligned}\varphi(y)=0 &\iff b\cdot y = \frac{y}{1+y}\\\\ &\iff b\cdot y \cdot (1+y) = y \\\\ &\iff y=0\quad\text{of}\quad b\,(1+y)=1 \\ \\ &\iff y=0\quad\text{of}\quad y=\frac{1}{b}-1\end{aligned}$$ Er zijn dus twee evenwichten. Om de aard van de evenwichten te achterhalen gebruiken we lokale linearisatie. We berekenen eerst de volgende afgeleide: $$\begin{aligned}\frac{\dd\varphi}{\dd y} &= b -\frac{\dd}{\dd y}\left(\frac{y}{1+y}\right) &\blue{\text{somregel voor differentiëren}}\\[0.25cm] &= b - \frac{(1+y)-y}{(1+y)^2} &\blue{\text{quotiëntregel voor differentiëren}} \\[0.25cm] &= b-\frac{1}{(1+y)^2}\end{aligned}$$ Omdat $\varphi'(0)=b-1$ volgt nu dat het evenwicht $y=0$ aantrekkend is als $b<1$, afstotend is als $b>1$ en semistabiel is als $b=1$. $$\begin{aligned}\varphi'\left(\frac{1}{b}-1\right) &= b - \frac{1}{\left(\frac{1}{b}\right)^2} \\\\ &= b-b^2 \\\\ &= b\,(1-b)\end{aligned}$$ Omdat de laatste uitdrukking een bergparabool in $b$ is met nulpunten bij $b=0$ en $b=1$, volgt dat het evenwicht $y=\frac{1}{b}-1$ afstotend is als $0<b<1$, semistabiel is $b=1$, en verder aantrekkend is.

We vatten het stabiliteitsonderzoek samen:

Als $b<0$ dan zijn er aantrekkende evenwichten $y=\frac{1}{b}-1$ en $y=0$, en deze liggen verder van elkaar af naarmate $b$ dichter bij $0$ is.

Als $b=0$ dan is er één evenwicht $y=0$ en dat is aantrekkend.

Als $0<b<1$ dan is $y=0$ een aantrekkend evenwicht en is $y=\frac{1}{b}-1$ een afstotend evenwicht.

Als $b=1$ dan is er één evenwicht $y=0$ en dat is semistabiel.

Als $b>1$ dan is $y=0$ een afstotend evenwicht en is $y=\frac{1}{b}-1$ een aantrekkend evenwicht.

De toestandslijnen in bovenstaande gevallen zijn achtereenvolgens

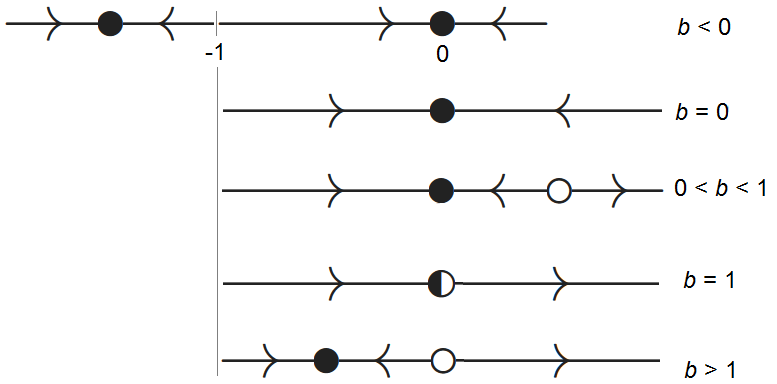
We hebben de toestandslijnen in bovenstaande figuur dusdanig verschoven dat de positie van de evenwichten ten opzichte van elkaar beter te zien is.

Het bifurcatiediagram kan geschetst worden of m.b.v. wiskundige software getekend worden. Het ziet er als volgt uit:

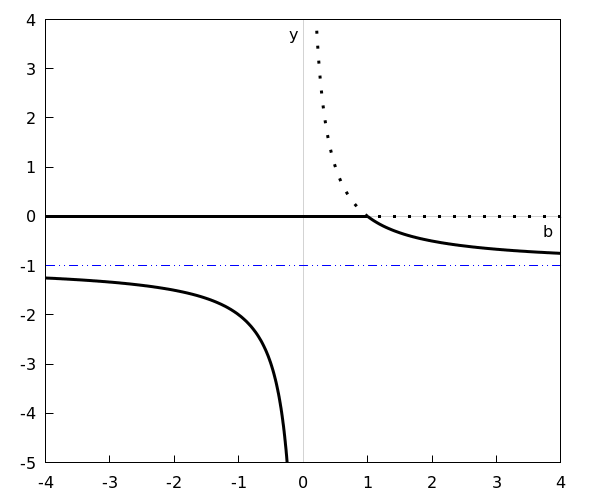
De horizontale blauwe lijn geeft $y=-1$ aan. De bifurcatie $b=1$ is een transkritische bifurcatie omdat de stabiliteit van evenwichten op dit punt verwisselt.