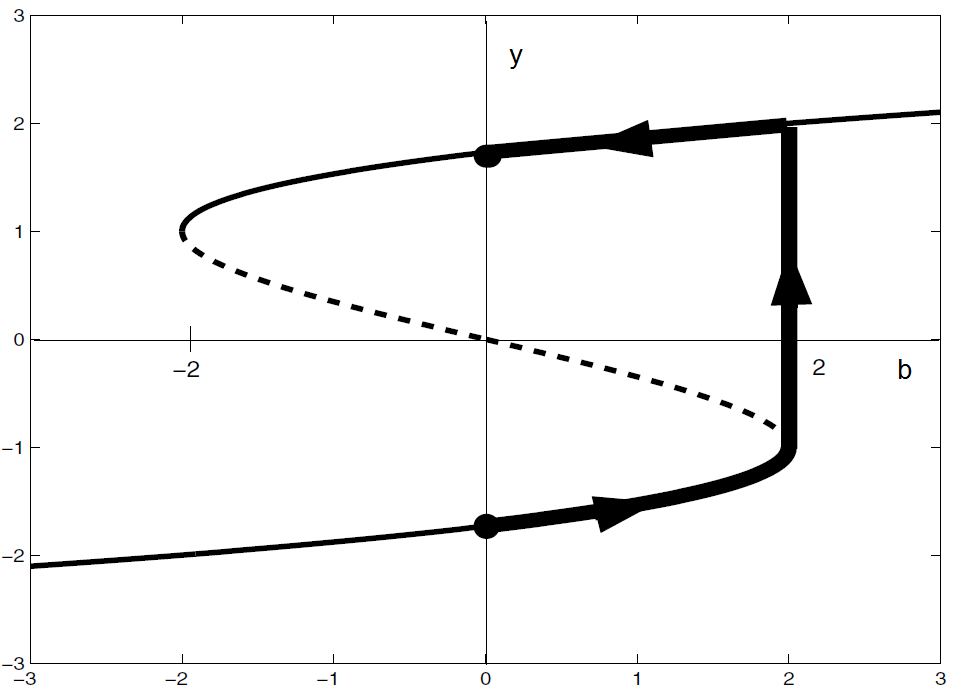
We consider the differential equation $$\frac{\dd y}{\dd t}= 3y-y^3+b$$ If $b=0$ then we find the equilibria by detecting the roots of the cubic polynomial $-y^3+3y$. These are $y=0$ and $y=\pm\sqrt{3}$. By local linearization one can verify (do it yourself!) that $y=0$ is a repeller, and that $y=-\sqrt{3}$ and $y=\sqrt{y}$ are attractors. Because of the latter property we speak of a bistable differential equation.

The parameter $b$ shifts the cubic polynomial $-y^3+3y$ upwards or downwards. In such a translation, three roots of the cubic polynomial remain as long as $-2<b<2$.

If $b=2$ then $$\frac{\dd y}{\dd t}= -(y-2)(y+1)^2$$ and there are two equilibria: a semi-stable equilibrium $y=-1$ and a stable equilibirum $y=2$ (check the nature of the equilibria yourself!).

If $b=-2$ then $$\frac{\dd y}{\dd t}= -(y-2)(y+1)^2$$ and there are two equilibria: a semi-stable equilibrium $y=1$ and a stable equilibrium $y=-2$ (check the nature of the equilibria yourself!).

This implies that the two bifurcations $(-2,1)$ and $(2,-1)$ are saddle-node bifurcations.

With a larger translation $|b|>2$ there exists only one root of the polynomial $3y-y^3+b$ and this leads to a repelling equilibrium.

$\phantom{xxx}$

We explore what happens when we start with $b=0$ in the equilibrium $y=-\sqrt{3}$ and then gradually increase the parameter value $b$ with small steps and wait after each change until a new equilibrium has settled. With increasing $b$, the point $(b,y)$ first remains in the vicinity on the lower branch of the stable equilibria; the solution goes in the course of time to a new equilibirum in the neighbourhood of where it came form along the branch in bifurcation diagram where the point is present. This continues until we reach $b=2$ at a saddle-node bifurcation; as soon as $b$ is slightly greater than $2$, than the solution moves away to the stable equilibrium in the upper branch of the stable equilibria. When we now decrease the parameter value step by step to $b=0$, then the point $(b,y)$ remains on the upper branch of the stable equilibria and we arrive for $b=0$ at the equilibrium $y=\sqrt{3}$. The parameter value $b$ returned to its original value, but the equilibrium $y$ not! This phenomenon of lack of reversibility is called hysteresis. It is visualized in the figure below.