We bekijken de differentiaalvergelijking \[\frac{\dd y}{\dd t}= 3y-y^3+b\] Als \(b=0\), dan vinden we de evenwichten door de nulpunten van de derdegraadsveelterm \(-y^3+3y\) op te sporen. Dit zijn \(y=0\) en \(y=\pm\sqrt{3}\). Door lokale linearisatie is na te gaan (doe dat zelf!) dat \(y=0\) een afstotend evenwicht is, en dat \(y=-\sqrt{3}\) en \(y=\sqrt{y}\) aantrekkende evenwichten zijn. Vanwege de laatste eigenschap noemen we de differentiaalvergelijking bistabiel.

De parameter \(b\) verschuift de derdegraads veelterm \(-y^3+3y\) naar boven of naar beneden. Bij deze translatie blijven er drie nulpunten behouden zolang \(-2<b<2\).

Als \(b=2\), dan \[\frac{\dd y}{\dd t}= -(y-2)(y+1)^2\] en zijn er twee evenwichten: een semistabiel evenwicht \(y=-1\) en een stabiel evenwicht \(y=2\) (ga de aard van de evenwichten zelf na).

Als \(b=-2\), dan \[\frac{\dd y}{\dd t}= -(y-2)(y+1)^2\] en zijn er twee evenwichten: een semistabiel evenwicht \(y=1\) en een stabiel evenwicht \(y=-2\) (ga de aard van de evenwichten zelf na).

Dit impliceert dat de twee bifurcaties \((-2,1)\) en \((2,-1)\) zadelknoopbifurcaties zijn.

Bij een grotere translatie \(|b|>2\) blijft er nog maar één nulpunt voor de veelterm \(3y-y^3+b\) over en dit levert een aantrekkend evenwicht op.

\(\phantom{xxx}\)

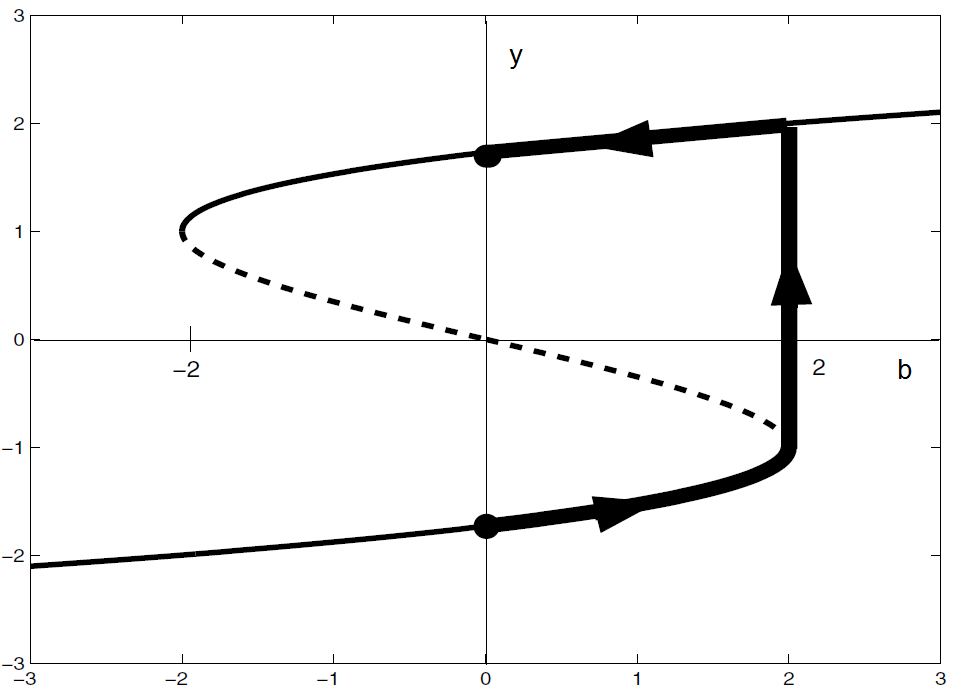
We bekijken nu wat er gebeurt als we starten met \(b=0\) in het evenwicht \(y=-\sqrt{3}\) en vervolgens de parameterwaarde \(b\) een beetje ophogen en wachten tot een nieuw evenwicht zich heeft ingesteld. Bij oplopende \(b\) blijft \((b,y)\) eerst in de buurt van de onderste tak van de stabiele evenwichten; de oplossing gaat na verloop van tijd naar een nieuw evenwicht in de buurt langs de tak in het bifurcatiediagram waar we op zitten. Dit gaat zo door totdat we bij \(b=2\) op een zadelknoopbifurcatie uitkomen; zodra \(b\) iets groter dan \(2\) wordt, dan loopt de oplossing naar het stabiele evenwicht in de bovenste tak van de stabiele evenwichten. Wanneer we nu de parameterwaarde weer laten zakken tot \(b=0\) blijft \((b,y)\) in de buurt van de bovenste tak van de stabiele evenwichten en komen we bij \(b=0\) uit op het evenwicht \(y=\sqrt{3}\). De parameterwaarde \(b\) is op zijn oorspronkelijke waarde teruggekomen, maar het evenwicht \(y\) niet! Dit fenomeen van gebrek aan omkeerbaarheid heet hysterese. Het is in onderstaande figuur gevisualiseerd.