Als biologische toepassing van een stabiliteitsanalyse van een dynamisch systeem bekijken we een terugkerende plaag van de Spruce Budworm populatie in Noord-Amerikaanse en Canadese naaldbossen. Het illustreert hoe een eenvoudig wiskundig model kan leiden tot beter begrip van de situatie en beter handelen. Voor details verwijzen we naar de bijgevoegde tekst (in pdf-formaat); hieronder geven we enkel een korte samenvatting.

André de Roos & Hans Heesterbeek (2004), Opkomst en ondergang: in de klem tussen bomen en vogels. In H. Heesterbeek, O. Diekmann, H. Metz (red.) De wiskundige kat, de biologische muis en de jacht op inzicht. Epsilon Uitgave, Utrecht.

Waar in Nederlandse zomers in de krant jaarlijks melding gemaakt wordt van een overlast door de Eikenprocessierups, verschijnen er in Noord-Amerikaanse en Canadese kranten om de 30 tot 40 jaar alarmberichten over de Spruce Budworm, een rups die zich graag tegoed doet aan naalden van sparren houdt en daardoor hele grote delen van bossen doet sterven.

Wat is aan de hand?

• Normaliter zitten er 5 Spruce Budwormen in een naaldboom;
• Vanaf de uitbraak van de insectenplaag stijgt in 5-6 jaar het aantal rupsen tot 20000 per boom;
• Door hoge dichtheid van de rupsenpopuatie ontstaat ontbladering en sterfte van bomen (9 jaar na de uitbraak);
• Na 14 jaar ongeveer 80% van alle bomen vernietigd;
• De Spruce Budworm populatie stort in door gebrek aan voedsel en predatie door vogels;
• Het bos herstelt;
• Het fenomeen herhaalt zich.

De economische schade van de rupsenplaag en bijkomende sterfte van naaldbossen is groot met betrekking tot toerisme en papierindustrie. Lange tijd leefde de gedachte dat de uitbraken van de insectenpopulatie het gevolg waren van klimatologische omstandigheden. Door gebruik van insecticiden probeerde men tevergeefs de insectenpopulatie in bedwang te houden: Bijvoorbeeld werd in 1976 nog 400000 \(\text{km}^2\) besproeid en in de periode 1952-1976 werd 95 miljoen dollar aan insecticiden besteed.

Een simulatiemodel met 30000 parameters hielp bij beheersmaatregelen, maar had maar in beperkte mate succes: bossen waren in 1976 weer in 'explosieve' toestand. Gelukking bood wetenschap uitkomst in 1978: een eenvoudig wiskundig model van Ludwig, Jones en Holling gaf een verklaring van de cyclische uitbraak van de Spruce Budworm populatie met vernietiging van grote stukken bos als gevolg. De belangrijkste conclusie m.b.v. dit model was dat periodieke uitbraken niet voorkomen kunnen worden, maar alleen in goede banen geleid worden.

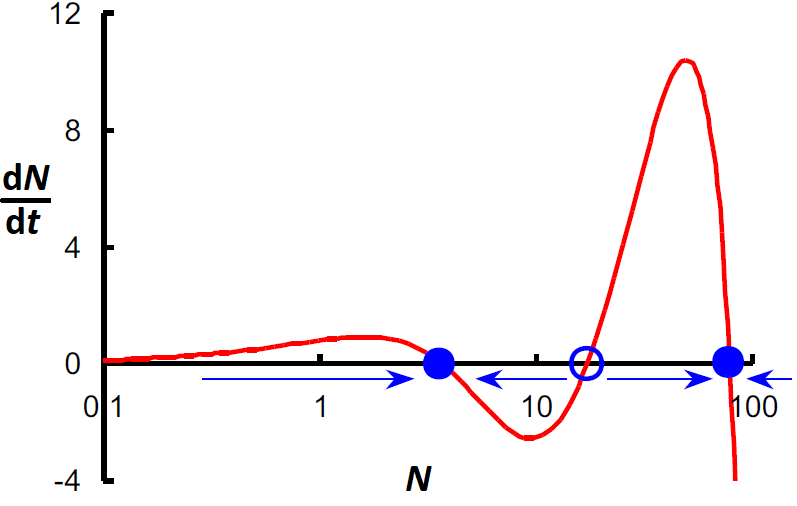
Het wiskundige model bestaat uit twee stukken: een logistisch groeimodel voor de populatiegroei en een Hill functie voor de populatiestefte ten gevolge van predatie door vogels in het bos. In formuletaal: \[\frac{\dd N}{\dd t}=r\cdot N\cdot\left(1-\frac{N}{K}\right)- \alpha\frac{N^2}{1+\beta N^2}\] met intrinsieke groeicoëfficiënt \(r\), draagkracht \(K\) en positieve constanten \(\alpha\) en \(\beta\) die de maximale predatie bepalen alsmede het buigpunt in de bijpassende predatiekromme. In onderstaand diagram is \(\dfrac{\dd N}{\dd t}\) uitgezet tegen \(N\) en kun je aflezen dat er twee aantrekkende evenwichten (bij \(N\approx 3\) en \(N\approx 20\)) zijn en een afstotend evenwicht (bij \(N\approx 10\) is. Dit alles bij de volgende parameterwaarden \(r=1.2\), \(K=100\), \(\alpha=0.4\), \(\beta=0.02\).

In het model wordt verder aangenomen dat de groeiparameters in het logistische deel van het model evenredig zijn met de oppervlakte \(A\) van het gebladerte, zeg \[r = \gamma\cdot A,\quad K =\frac{\phi}{\gamma}\cdot A\text{.}\] Dan geldt dus: \[\frac{\dd N}{\dd t}=\gamma\cdot A\cdot N-\phi\cdot N^2- \alpha\frac{N^2}{1+\beta N^2}\] We gaan nu bestuderen hoe de grafiek van \(\dfrac{\dd N}{\dd t}\) als functie van \(N\) er uit ziet en wat dat voor het aantal en de aard van de evenwichten betekent. In onderstaand diagram zijn deze grootheden tegen elkaar uitgezet voor verschillende waarden van \(A\), nl. \(A=25,35,45,55,65,75,85\), met \(\gamma= 0.0111\), \(\phi=0.009\), \(\alpha=0.5\), \(\beta=0.1\).

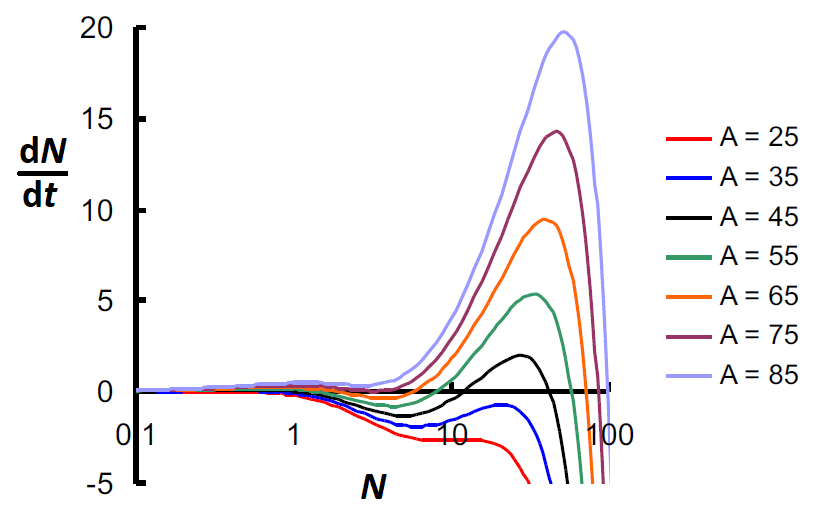
Voor kleine waarden van \(A\) is er alleen een nulpunt aan de linkerkant van de \(N\)-as dat bij een aantrekkend evenwicht hoort. Bij zeer hoge waarden van \(A\) is er ook maar één nulpunt horend bij een aantrekkend evenwicht. Bij middelmatige waarden van \(A\) zijn er 3 nulpunten horende bij twee aantrekkende evenwichten gescheiden door een afstotend evenwicht.

Als we de rechterkant van de differentiaalvergelijking \[\frac{\dd N}{\dd t}=\gamma\cdot A\cdot N-\phi\cdot N^2- \alpha\frac{N^2}{1+\beta N^2}\] gelijkstellen aan \(0\) om evenwichten \(N^{\ast}\) te vinden, dan kunnen we \(A\) als functie van \(N^{\ast}\) opschrijven: \[A = \frac{\phi\cdot N^{\ast}}{\gamma}-\frac{\alpha}{\gamma}\frac{N^{\ast}}{1+\beta {N^{\ast}}^2}\] De grafiek van dit verband kunnen we spiegelen in de lijn \(y=x\), zodat \(N^{\ast}\) uitgezet is tegen \(A\). Dit levert een zogenaamd bifurcatiediagram op met voor iedere parameterwaarde \(A\) uitgezet de aantrekkende evenwichten (gesloten cirkels) en de afstotende evenwichten (open cirkels):

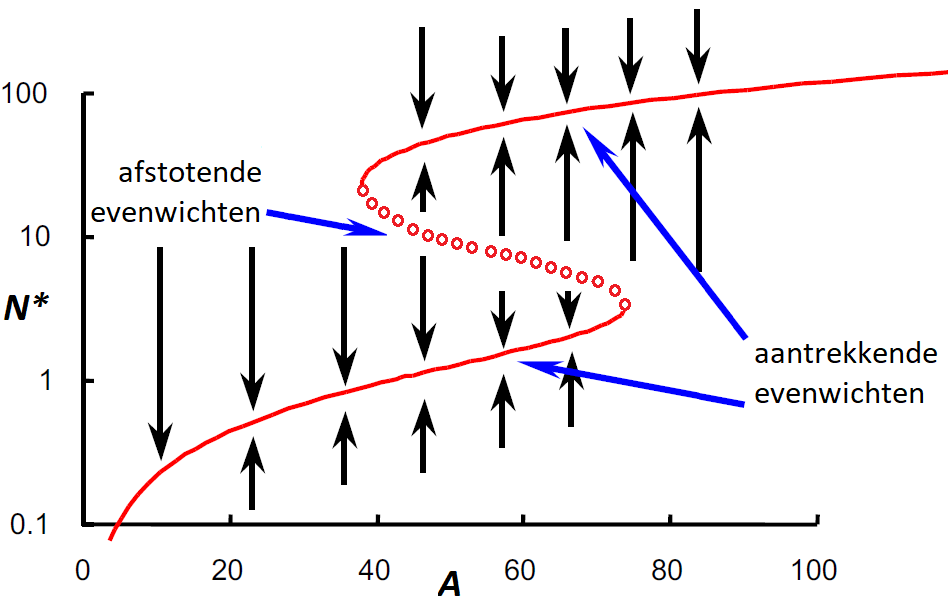
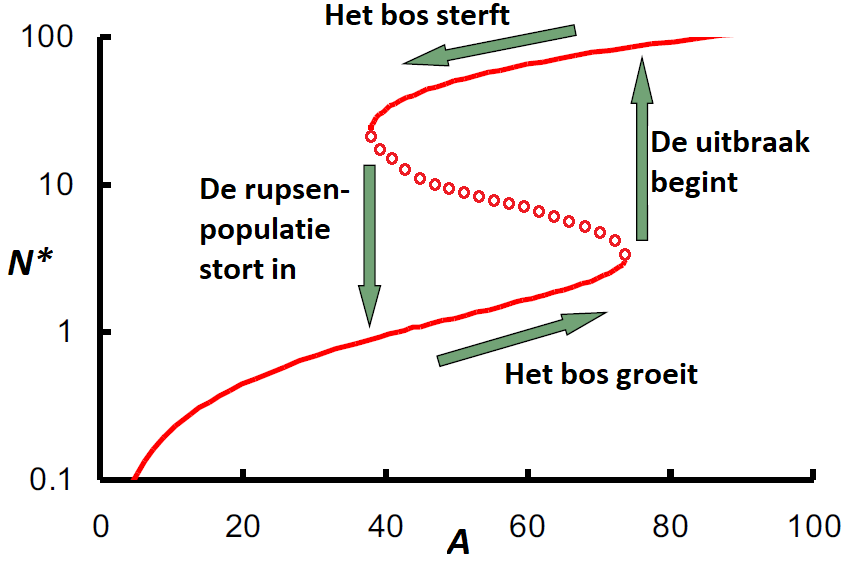
Merk op dat wanneer \(A\) toeneemt, bij een overschrijding van de waarde \(A\approx 75\) plotsklaps er nog maar één aantrekkend evenwicht bij een hogere waarde van \(N^{\ast}\) optreedt. Dit is de uitbraak van de insectenplaag. Evenzo is een kleine verlaging rondom \(A\approx 40\) voldoende om de rupsenpopulatie in te laten storten.

Onderstaande figuur vat het scenario van een cyclische insectenplaag samen. De uitbraak en ineenstorting van de Spruce Budworm populatie past bij de zogeheten kantelpunten in het bifurcatiediagram.