We consider an application of the stability analysis of a differential equation of the form \(y'=\varphi(y)\) in neural models that describe an action potential of an excitable cell. We will use the persistent sodium model, i.e., the \(I_{\text{Na, p}}\) Eugene Izhikevich, described in his standard work Dynamical Systems in Neuroscience.

This model is a reduction of the Hodgkin-Huxley model to only the sodium channel and the leakage channel, with no inactivation components (hence the name persistent), and only one activation component: \[\begin{aligned}C\frac{\dd V}{\dd t} &= -\overline{g_\mathrm{Na}}\cdot m\cdot (V-E_\mathrm{Na}) - g_\mathrm{L}\cdot (V-E_\mathrm{L})\\[0.25cm] \tau(V)\cdot \frac{\dd m}{\dd t}&= m_{\infty}(V)-m\end{aligned}\] If we now assume that the voltage-dependent time constant \(\tau(V)\) is very small, i.e., that the function \(m\) in a very short time reaches the value \(m_{\infty}(V)\), we get one ODE: \[C\frac{\dd V}{\dd t} = I -\overline{g_\mathrm{Na}}\cdot m_{\infty}(V)\cdot (V-E_\mathrm{Na}) - g_\mathrm{L}\cdot (V-E_\mathrm{L})\] with \[m_{\infty}(V)=\frac{1}{1+\exp\left(\dfrac{V_{1/2}-V}{k}\right)}\] where the parameter \(V_{1/2}\) satisfies \(m_\infty(V_{1/2})=0.5\) and \(k\) is a constant that indicates how fast \(m_\infty(V)\) changes with respect to the voltage \(V\). Smaller values of \(|k\) result in steeper graphs of \(m_\infty(V)\).

Henceforth we assume the following parameter values that hold for a pyramidal neuron in the fifth layer of the primary visual cortex of a rat at room temperature: \[\begin{array}{llll}C=10\,\text{µF} & I=0\,\text{pA} & g_\mathrm{L}=10\,\text{mS} & E_\mathrm{L}=-67\,\text{mV} \\ \overline{g_\mathrm{Na}}=74\,\text{mS} & V_{1/2}=1.5\,\text{mV} & k=16\,\text{mV} & E_\mathrm{Na}=60\,\text{mV}\end{array}\]

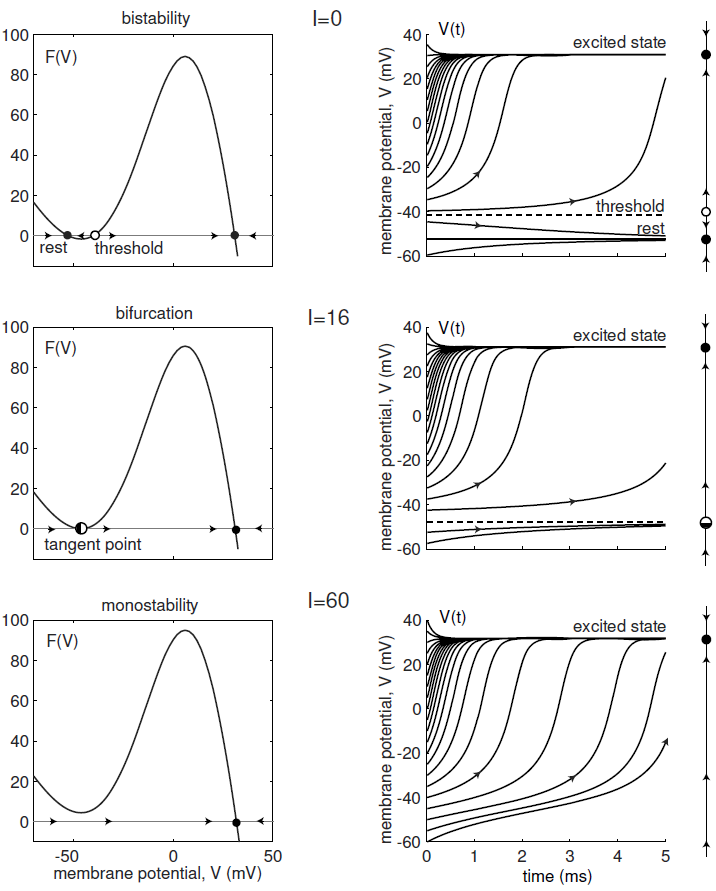
We can now write the ODE as \[\frac{\dd V}{\dd t}=\varphi(V)\] with the following graph of \(\varphi(V)\)

There are three equilibria: \(V=-52.4\,\text{mV},\quad V=-40.3\,\text{mV},\quad V=30.9\,\text{mV}\). The potential \(V=-52.4\,\text{mV}\) is an attractor and corresponds with the resting membrane potential. The potential \(V=30.9\,\text{mV}\) is also an attractor and corresponds with an excited state. So, for \(I=0\) there exist at the same time two stable equilibria and the solution curve reaches one of the two equilibria, depending on the start value \(V(0)\). The unstable equilibrium \(V=-40.3\,\text{mV}\) is the threshold potential above which excitation takes place.

With a sufficiently large stimulus, for example \(I=60\,\text{pA}\), the graph of shifts \(\varphi(V)\) is shifted upwards and the local minimum comes to lie above zero. In that case, there is only one equilibrium and that is attracting. The two situations are shown below in graph form, in which the solution curves are shown for different initial values.

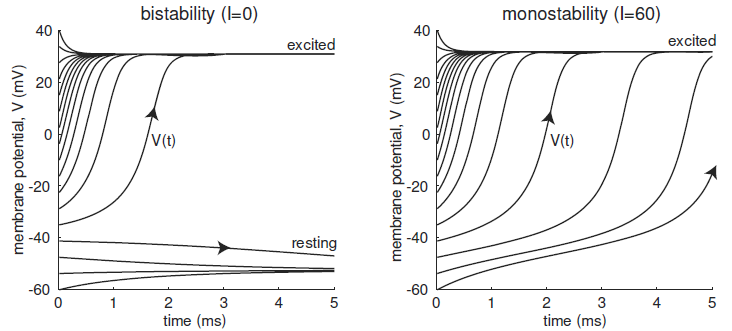
The bifurcation value at which the behaviour of solutions of the differential equation changes found to be about \(15.8\,\text{pA}\).