We bekijken een toepassing van het stabiliteitsonderzoek van een differentiaalvergelijking van de vorm $y'=\varphi(y)$ in neurale modellen die een actiepotentiaal van een exciteerbare cel beschrijven. We gebruiken hiervoor het persistente natriummodel oftewel het $I_{\text{Na, p}}$ van Eugene Izhikevich, beschreven in zijn boek Dynamical Systems in Neuroscience.

Dit model is een reductie van het Hodgkin-Huxley model tot enkel het natrium kanaal en het lekkanaal, met daarbij geen inactivatie-componenten (vandaar de naam persistent) en maar één activatie-component: $$\begin{aligned}C\frac{\dd V}{\dd t} &= -\overline{g_\mathrm{Na}}\cdot m\cdot (V-E_\mathrm{Na}) - g_\mathrm{L}\cdot (V-E_\mathrm{L})\\[0.25cm] \tau(V)\cdot \frac{\dd m}{\dd t}&= m_{\infty}(V)-m\end{aligned}$$ Als we nu veronderstellen dat de spanningsafhankelijke tijdconstante $\tau(V)$ zeer klein is, dat wil zeggen dat de functie $m$ in zeer korte tijd de waarde $m_{\infty}(V)$ aanneemt, dan krijgen we één GDV: $$C\frac{\dd V}{\dd t} = I -\overline{g_\mathrm{Na}}\cdot m_{\infty}(V)\cdot (V-E_\mathrm{Na}) - g_\mathrm{L}\cdot (V-E_\mathrm{L})$$ met $$m_{\infty}(V)=\frac{1}{1+\exp\left(\dfrac{V_{1/2}-V}{k}\right)}$$ waarbij de parameter $V_{1/2}$ voldoet aan $m_\infty(V_{1/2})=0.5$ en $k$ een constante is die aangeeft hoe snel $m_\infty(V)$ verandert m.b.t. de spanning $V$. Kleinere waarden van $|k|$ resulteren in stijlere grafieken van $m_\infty(V)$.

We nemen in het vervolg de volgende parameterwaarden horende bij een pyramidaal neuron in de vijfde laag van de primaire visuele cortex van een rat bij kamertemperatuur: $$\begin{array}{llll}C=10\,\text{µF} & I=0\,\text{pA} & g_\mathrm{L}=10\,\text{mS} & E_\mathrm{L}=-67\,\text{mV} \\ \overline{g_\mathrm{Na}}=74\,\text{mS} & V_{1/2}=1.5\,\text{mV} & k=16\,\text{mV} & E_\mathrm{Na}=60\,\text{mV}\end{array}$$

We kunnen de GDV nu schrijven als $$\frac{\dd V}{\dd t}=\varphi(V)$$ met de volgende grafiek van $\varphi(V)$

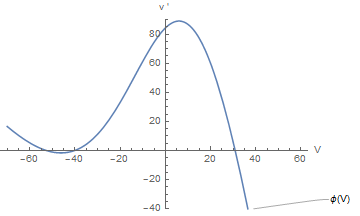
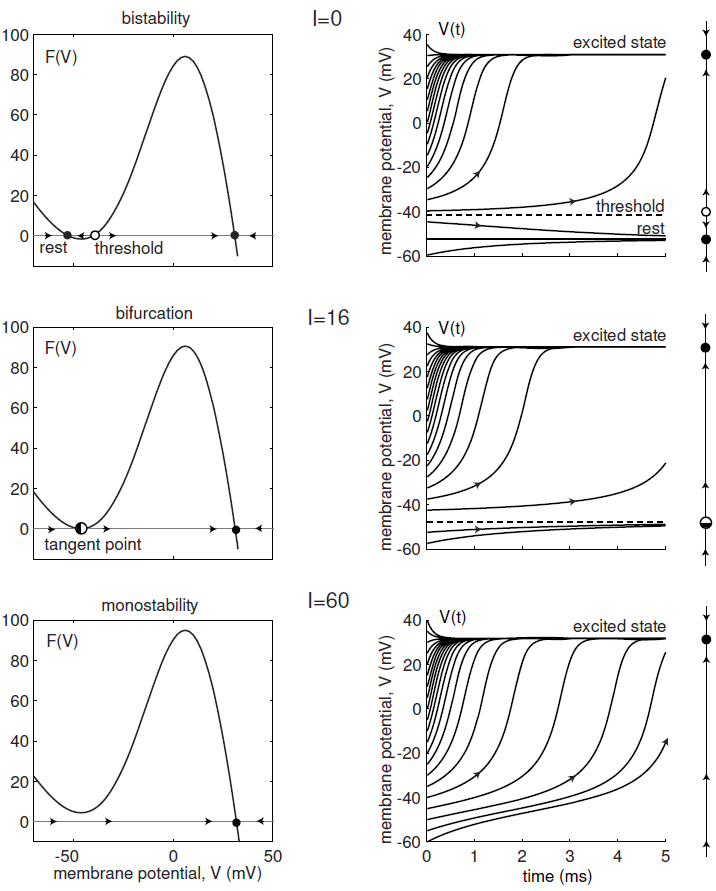
Er zijn drie evenwichten: $V=-52.4\,\text{mV},\quad V=-40.3\,\text{mV},\quad V=30.9\,\text{mV}$. De potentiaal $V=-52.4\,\text{mV}$ is een aantrekkend evenwicht en hoort bij de rustmembraanpotentiaal. De potentiaal $V=30.9\,\text{mV}$ is een aantrekkend evenwicht en hoort bij een geëxciteerde toestand. Er bestaan dus voor $I=0$ tegelijkertijd twee stabiele evenwichten en afhankelijk van de startwaarde $V(0)$ nadert de oplossingskromme één van de twee evenwichten. Het instabiele evenwicht $V=-40.3\,\text{mV}$ is de drempelwaarde waarboven excitatie plaats vindt.

Bij een voldoende grote stimulus, bijvoorbeeld $I=60\,\text{pA}$, verschuift de grafiek van $\varphi(V)$ naar boven en komt het lokale minimum boven nul te liggen. In dat geval is er maar één evenwicht en dat is aantrekkend. De twee situaties staan hieronder in grafiekvorm, waarbij oplossingskrommen bij verschillende startwaarden getekend zijn.

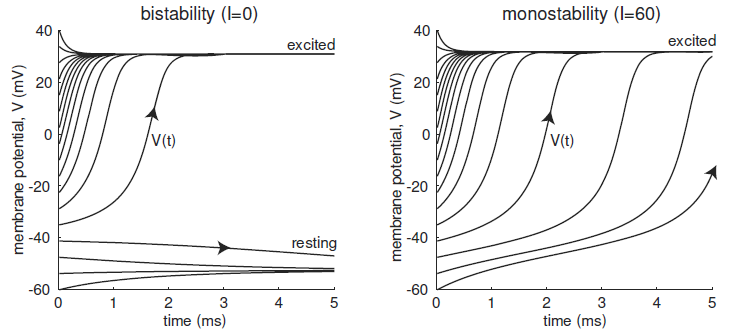
De bifurcatiewaarde waarop het gedrag van oplossingen van de differentiaalvergelijking verandert blijkt ongeveer $15.8\,\text{pA}$.