Ordinary differential equations: Separable differential equations
 Overview of growth models
Overview of growth models
We have explored the following growth models, of which many can be solved by separation of variables (in the figures \(y_0 = 0.1\); \(r=1\); \(a=4\);\(b=1\) was used):
| Name | Differential equation | Solution | Graph |
| Linear growth | \[ y' = r \] | \[ y(t) = r \cdot t + y_0 \] | 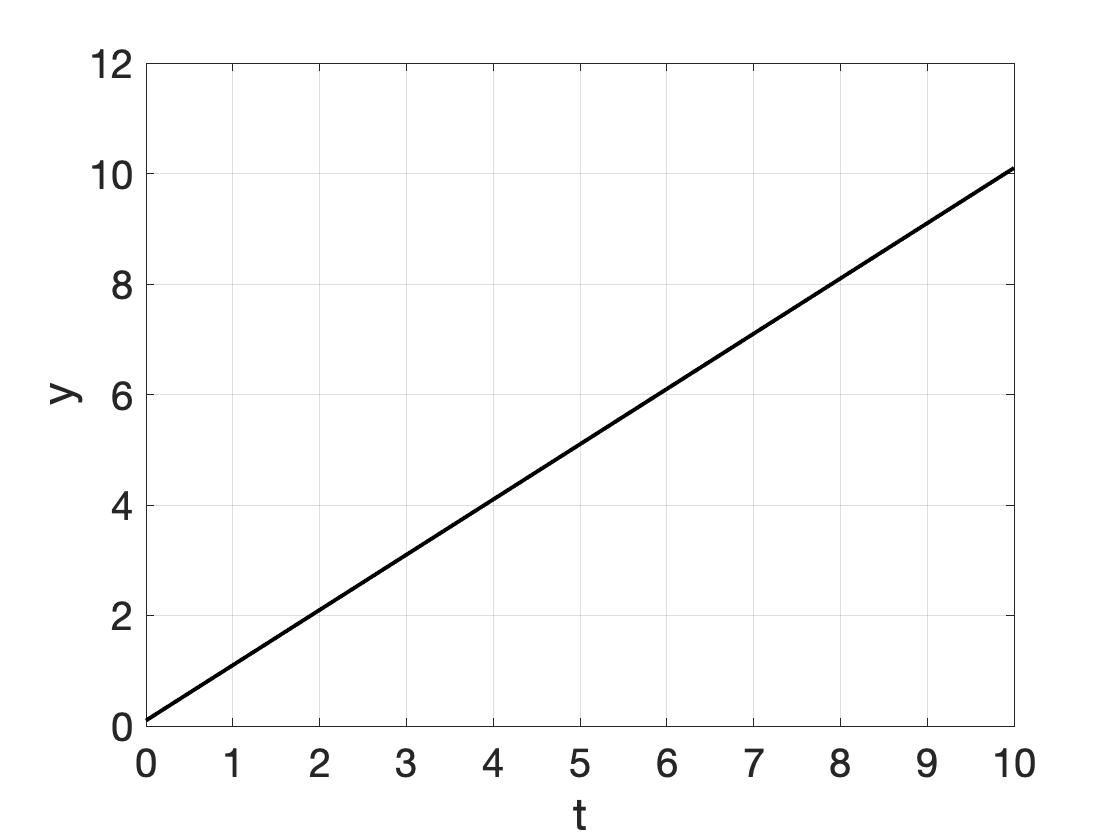 |
| Quadratic growth | \[ y'' = 2 \cdot r \] | \[ y(t) = r \cdot t^2 + b \cdot t+y_0 \] | 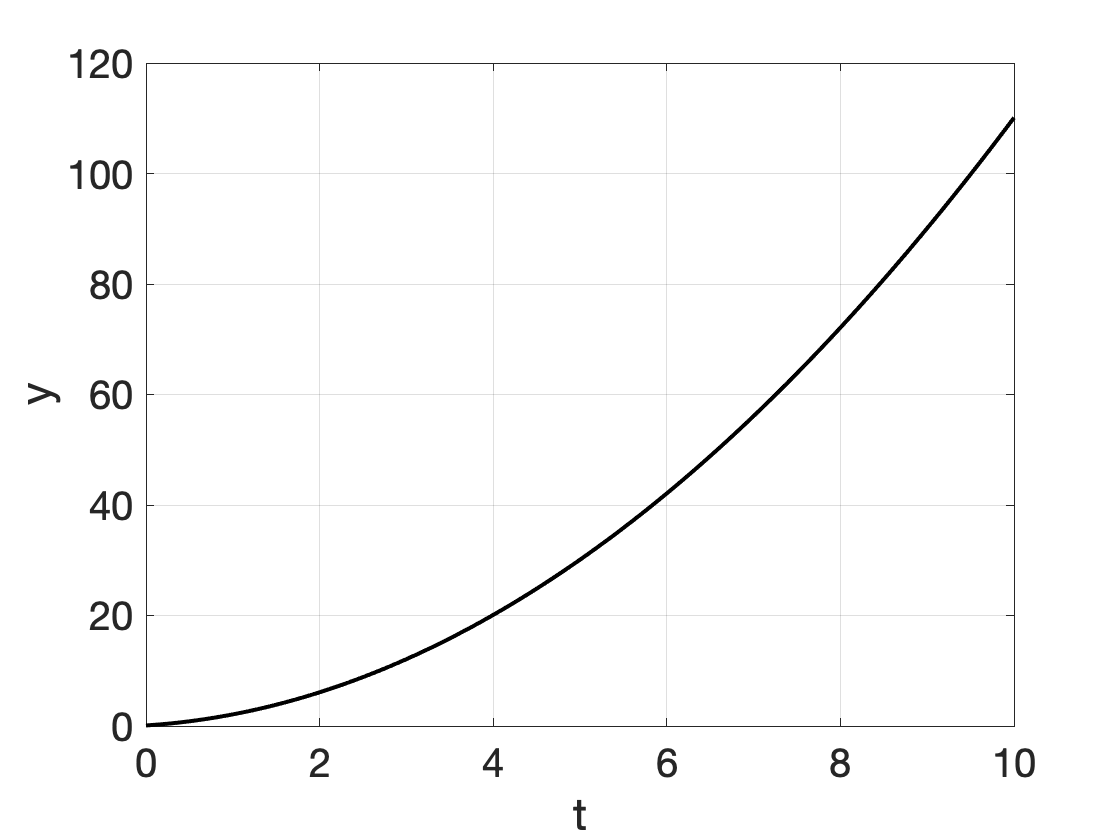 |
| Exponential growth | \[ y' = r \cdot y \] | \[ y(t) = y_0 \cdot e^{r \cdot t} \] | 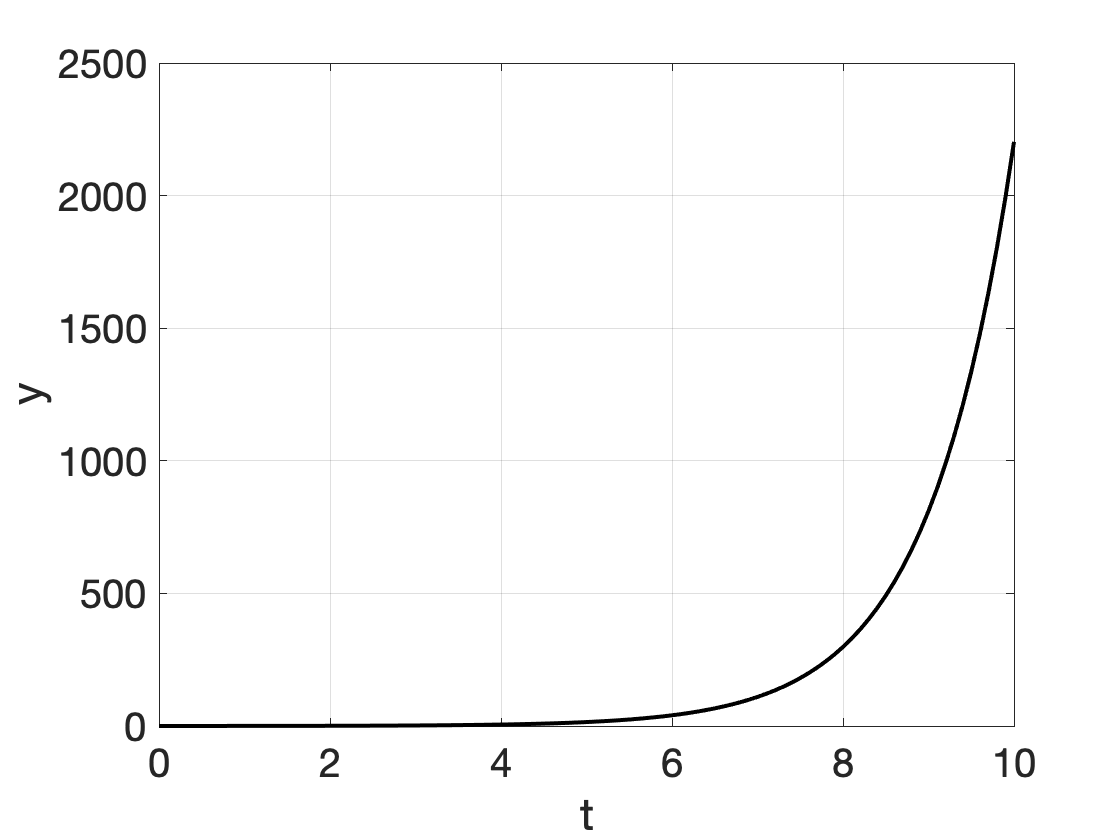 |
| Restricted exponential growth | \[ y' = r \cdot (a-y) \] | \[ y(t) = a-(a-y_0)\cdot e^{-r \cdot t} \] | 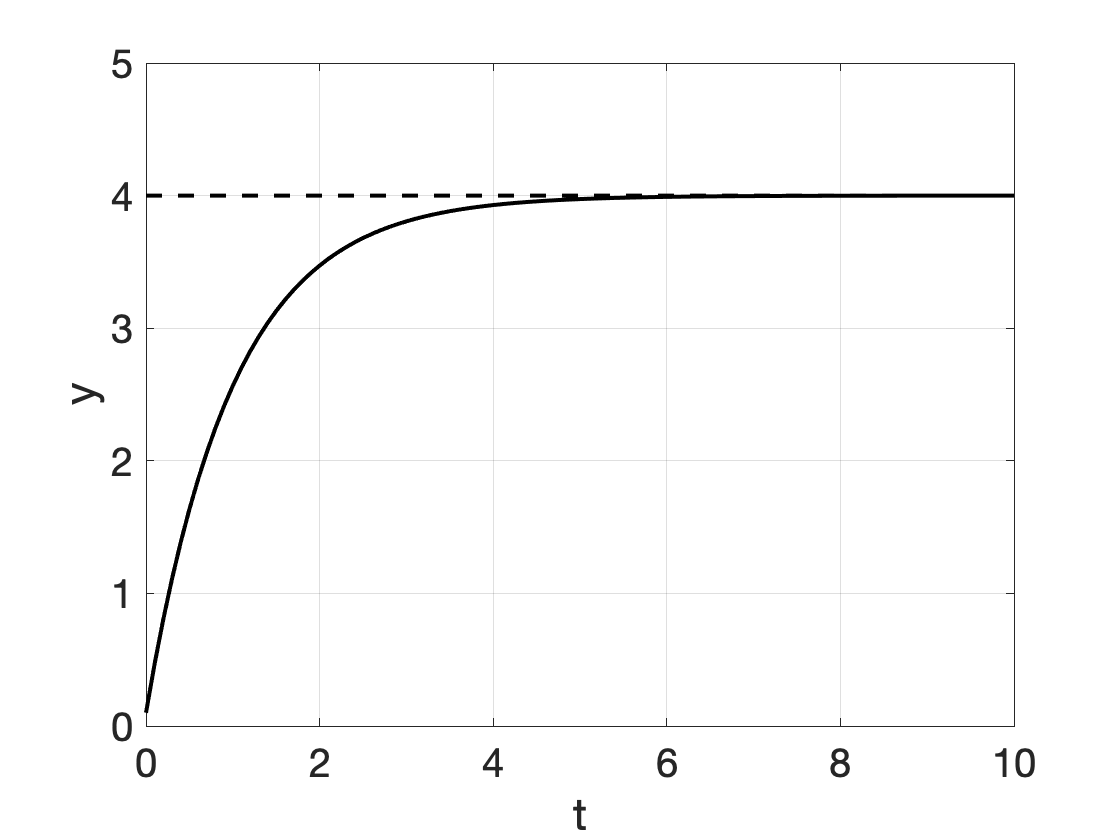 |
| Gompertz growth* | \[ y' = r \cdot y \cdot e^{-a \cdot t} \] | \[ y(t) = y_0 e^{\frac{r}{a}\cdot (1-e^{-a \cdot t})}\] | 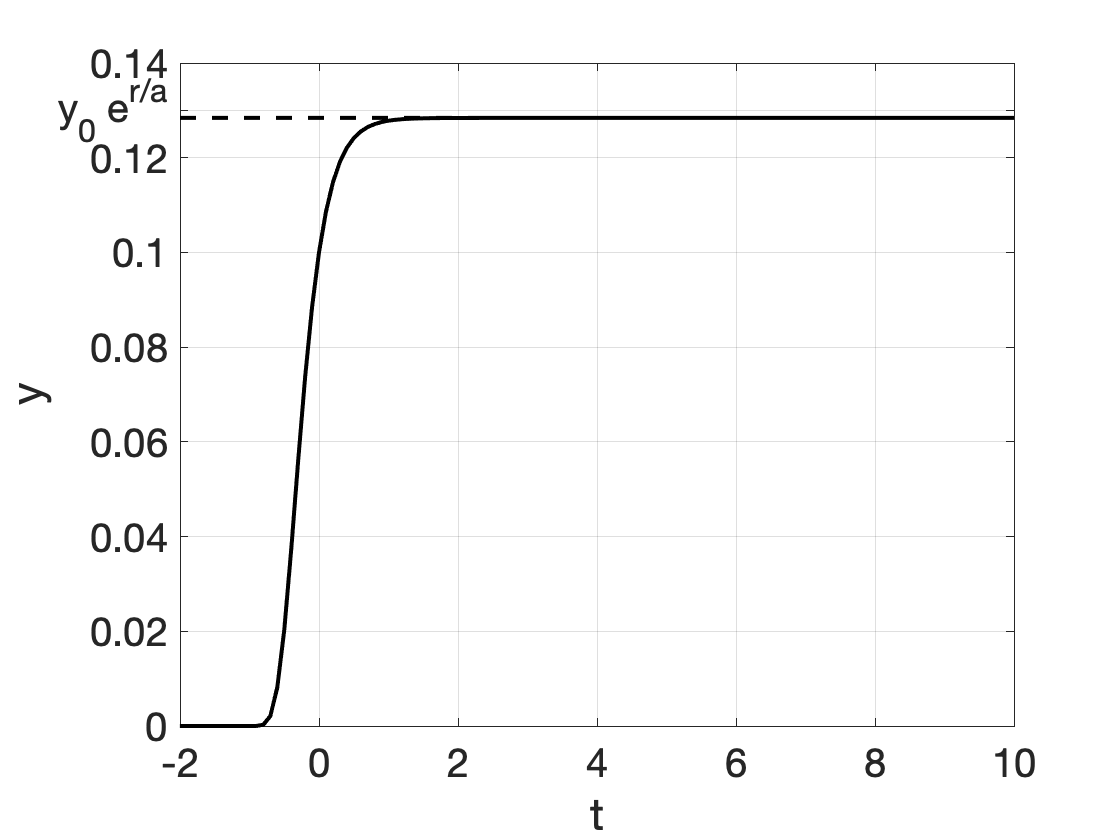 |
| Logistic growth | \[ y'= r \cdot y \cdot (1-\frac{y}{a})\] | \[ y(t) = \frac{a}{1 + (\frac{a}{y_0}-1)\cdot e^{-r \cdot t}} \] | 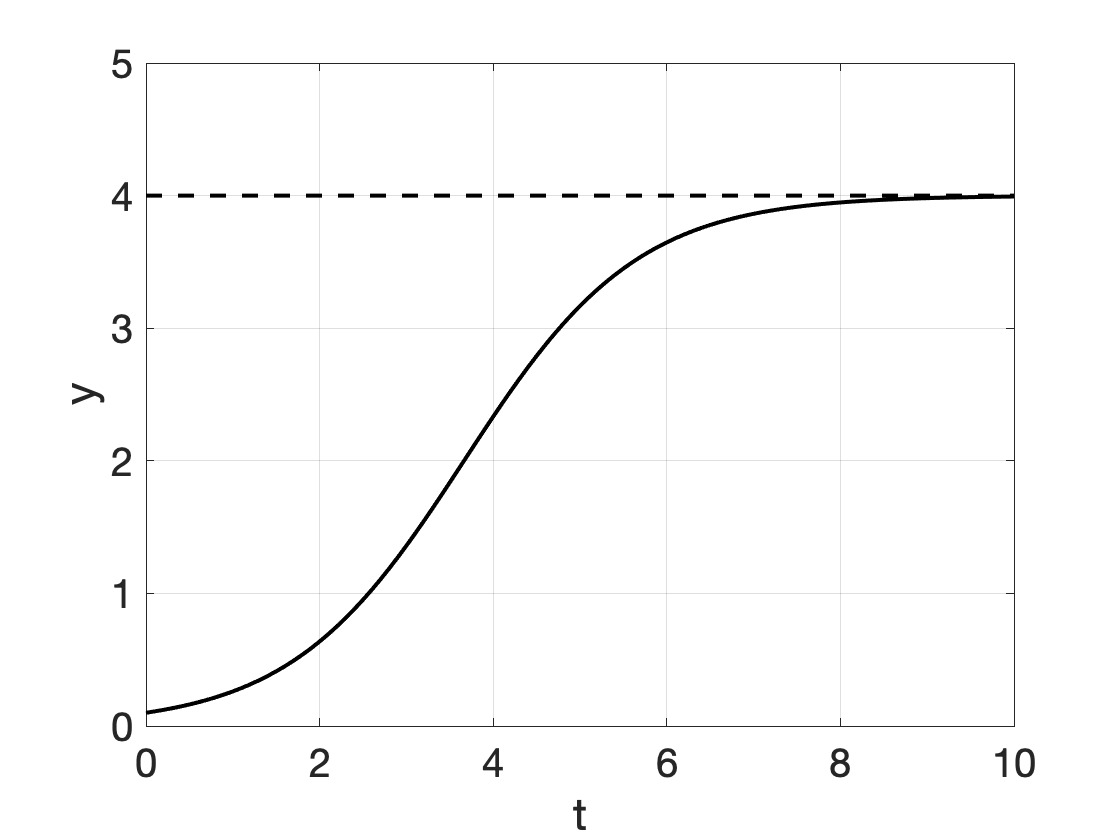 |
With these models, you now have quite a set of tools to model the growth of populations, the dynamics of chemical reactions, or neural activity.
* Note that the Gompertz model is defined in different ways in the literature. Another form of the Gompertz model (for instance at Wikipedia) you might encounter is
| Gompertz growth II | \[ y' = r \cdot y \cdot \ln(\frac{a}{y}) \] |
\[ y(t) = a \left(\frac{a}{y_0} \right)^{-e^{-r \cdot t}}\] \[= a^{1-e^{-r \cdot t}}\cdot y_0^{e^{-r \cdot t}} \] |
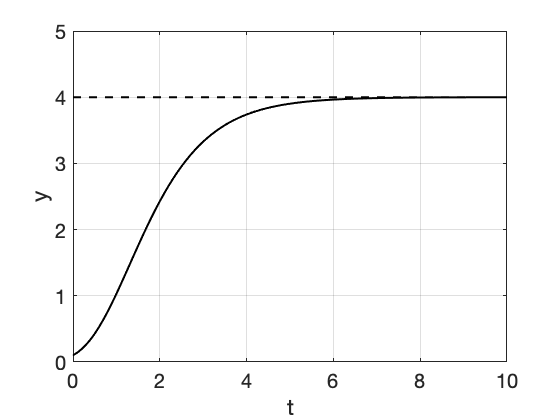 |
Unlock full access



