Gewone differentiaalvergelijkingen: Scheiden van variabelen
 Overzicht van groeimodellen
Overzicht van groeimodellen
We hebben de volgende groeimodellen ondrzocht, waarvan er veel kunnen worden opgelost door scheiding van variabelen (in de figuren \(y_0 = 0.1\), \(r=1\), \(a=4\); \(b=1\) werd gebruikt):
| Naam | Differentiaalvergelijking | Oplossing | diagram |
| Lineaire groei | \[ y' = r \] | \[ y(t) = r \cdot t + y_0 \] | 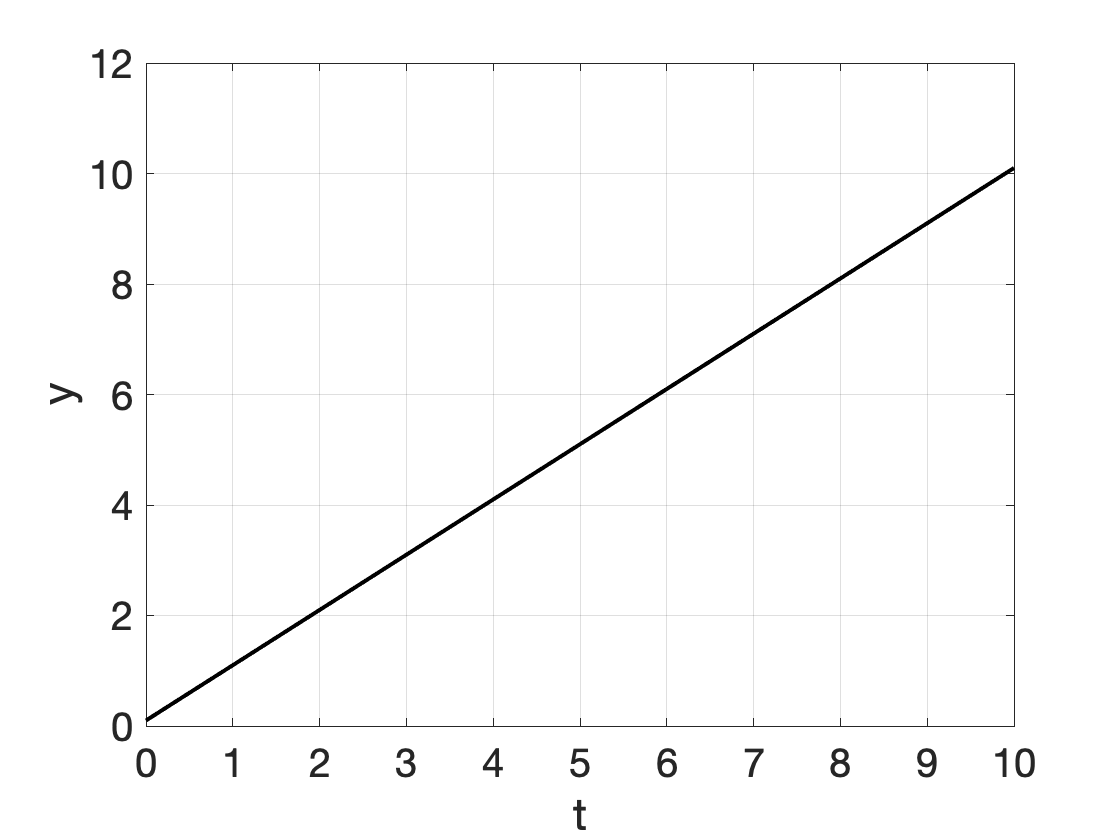 |
| Kwadratische groei | \[ y'' = 2 \cdot r \] | \[ y(t) = r \cdot t^2 + b \cdot t+y_0 \] | 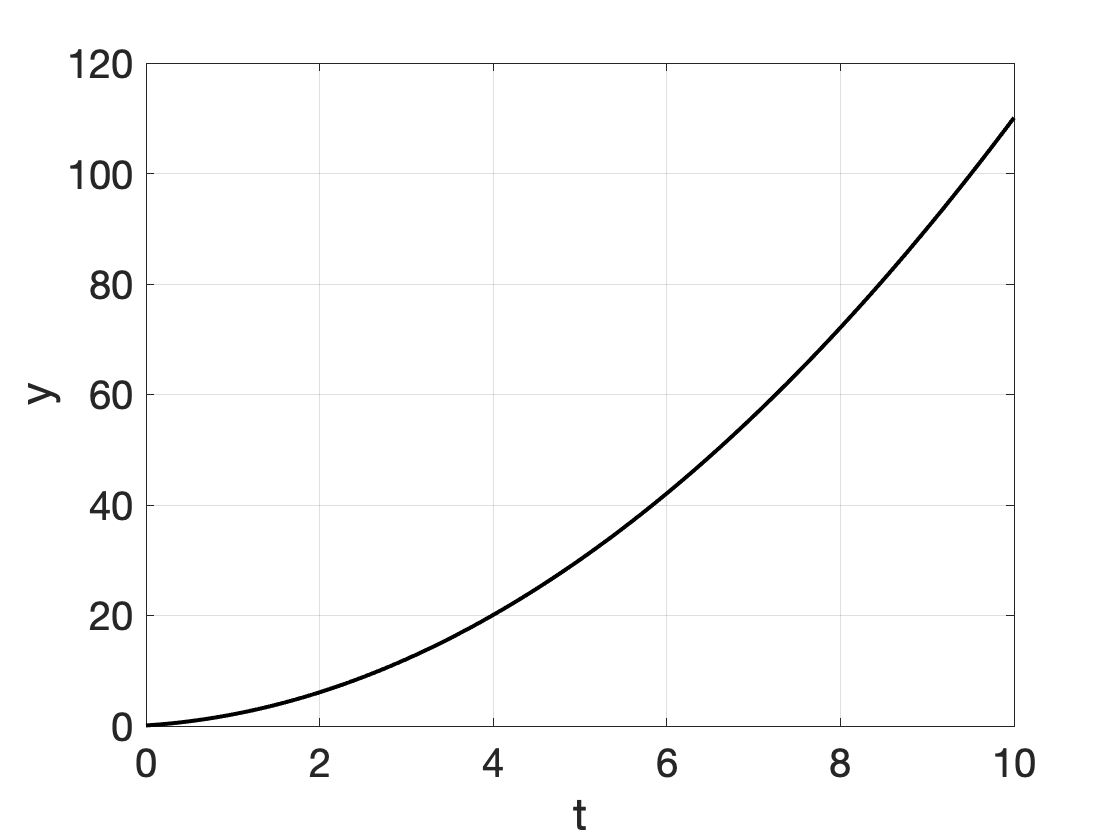 |
| Exponentiële groei | \[ y' = r \cdot y \] | \[ y(t) = y_0 \cdot e^{r \cdot t} \] | 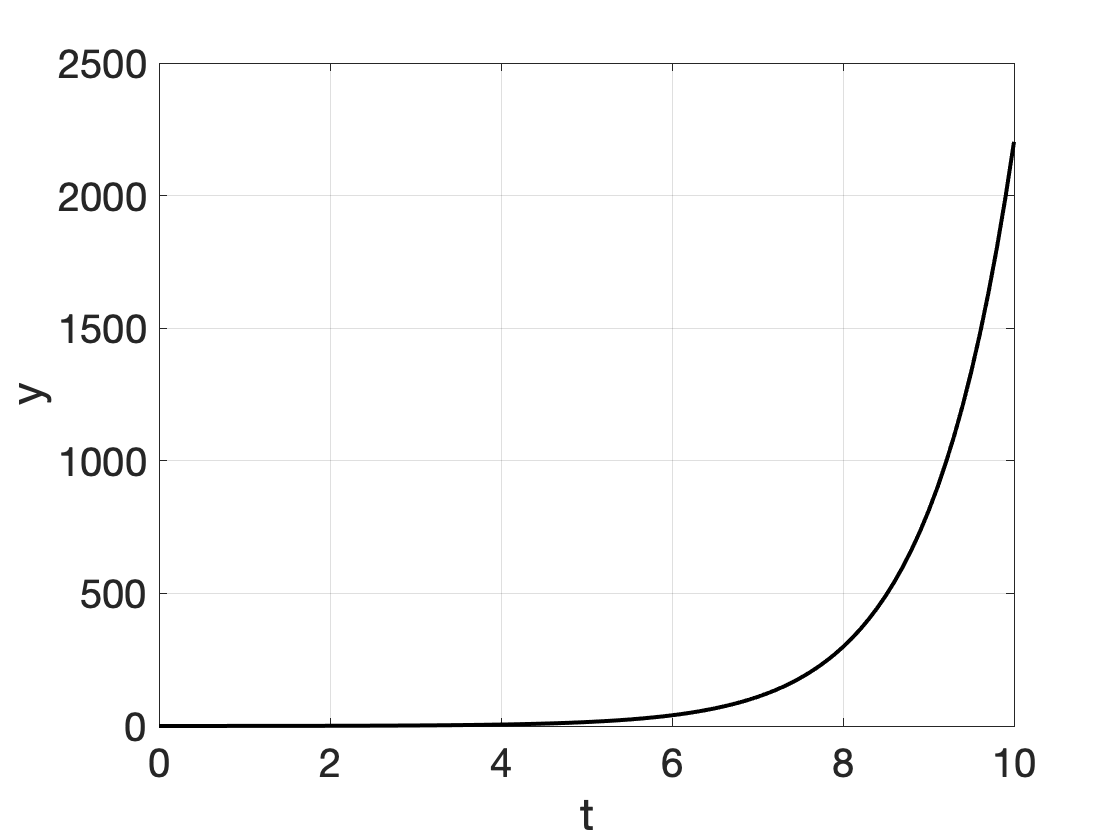 |
| Begrensde exponentiële groei | \[ y' = r \cdot (a-y) \] | \[ y(t) = a-(a-y_0)\cdot e^{-r \cdot t} \] | 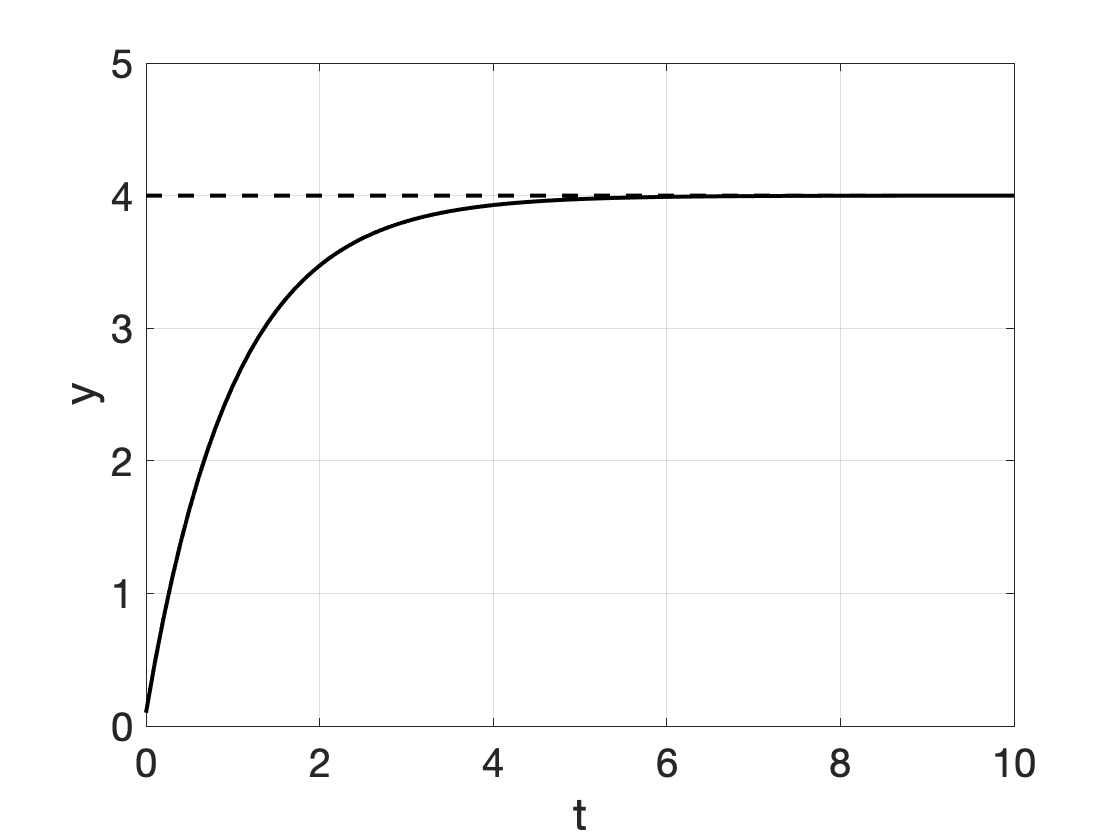 |
| Gompertz groei * | \[ y' = r \cdot y \cdot e^{-a \cdot t} \] | \[ y(t) = y_0 e^{\frac{r}{a}\cdot (1-e^{-a \cdot t})}\] | 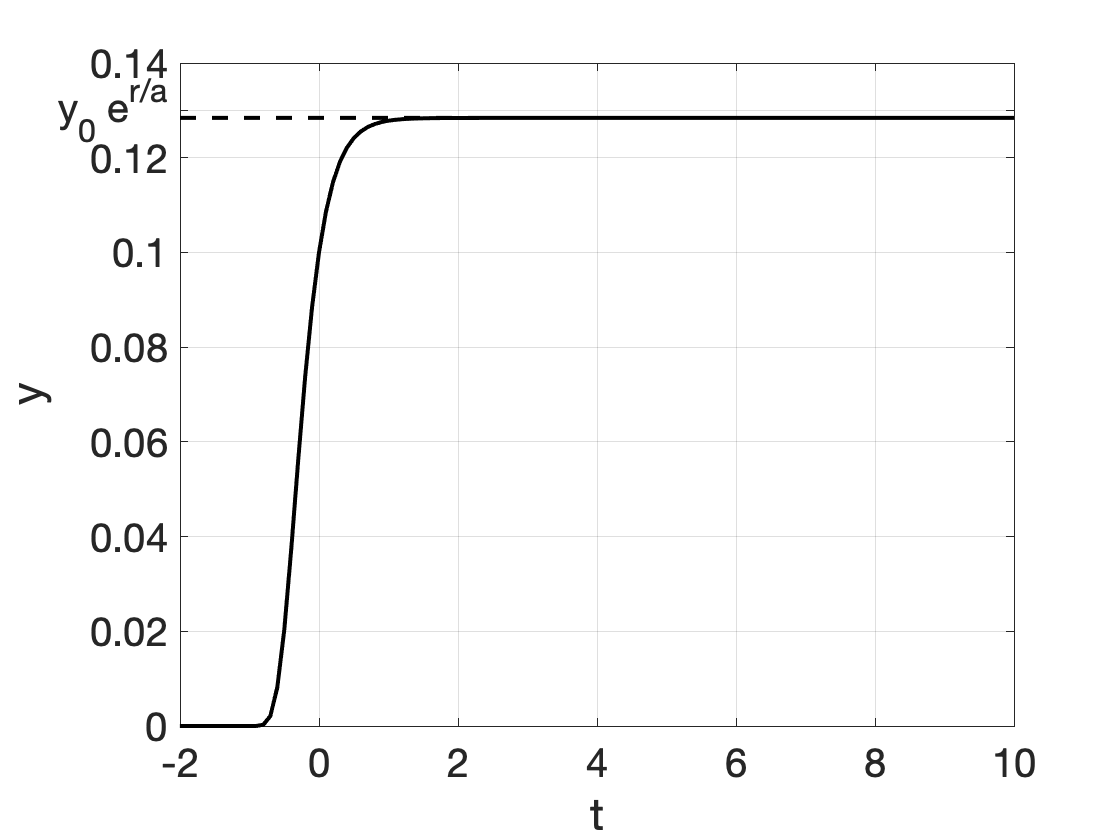 |
| logistische groei | \[ y'= r \cdot y \cdot (1-\frac{y}{a})\] | \[ y(t) = \frac{a}{1 + (\frac{a}{y_0}-1)\cdot e^{-r \cdot t}} \] | 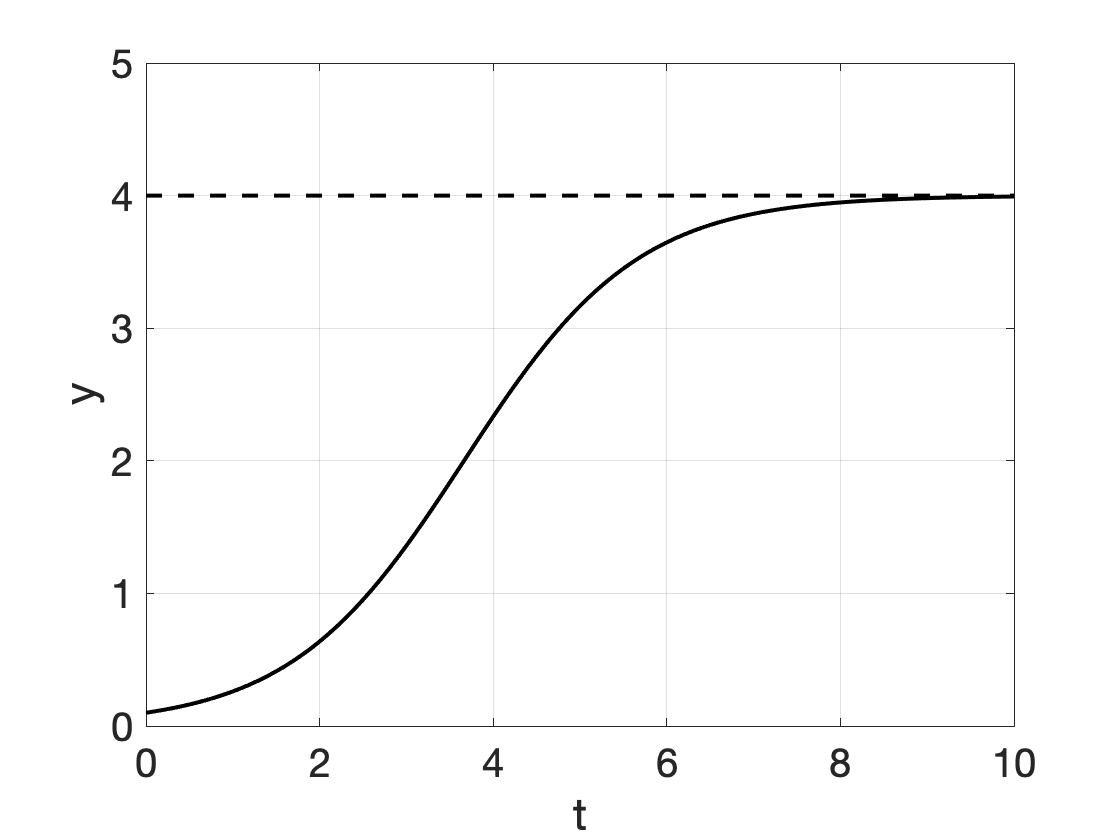 |
Met deze modellen heb je nu een heel arsenaal van gereedschappen om de groei van een populatie, de dynamica van chemische reacties, of neurale activiteit te modelleren.
* Merk op dat het Gompertz model op verschillende manieren gedefinieerd wordt in de literatuur. Een andere vorm van de Gompertz model (bijvoorbeeld bij Wikipedia ) die u kunt tegenkomen is
| Gompertz groei II | \[ y' = r \cdot y \cdot \ln(\frac{a}{y}) \] |
\[ y(t) = a \left(\frac{a}{y_0} \right)^{-e^{-r \cdot t}}\] \[= a^{1-e^{-r \cdot t}}\cdot y_0^{e^{-r \cdot t}} \] |
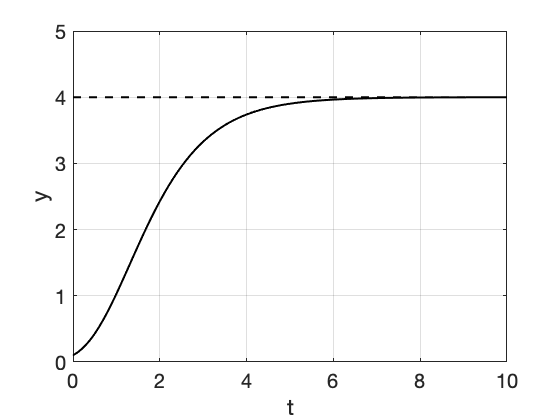 |
Ontgrendel volledige toegang



