We consider the periodic continuation of the function $$f(x)=\begin{cases} -\pi & \text{if }-\pi\le x<0, \\ \pi & \text{if }0\le x<\pi\end{cases}$$ The Fourier sine coefficients are $$\begin{aligned}b_n &=\frac{1}{\pi}\int_{-\pi}^{\pi} f(x)\sin(nx)\,\dd x \\ \\ &= -\int_{-\pi}^{0} \sin(nx)\,\dd x + \int_{0}^{\pi} \sin(nx)\,\dd x \\ \\ &= 2\int_{0}^{\pi} \sin(nx)\,\dd x \\ \\ &= 2\Bigl[\frac{-\cos(nx)}{n}\Bigr]_{0}^{\pi} \\ \\ &= \frac{2\bigl(1-\cos(n\pi)\bigr)}{n} \\ \\ &= \begin{cases} 0 & \text{if }n\text{ is even} \\ \\ \dfrac{4}{n} & \text{if }n\text{ is odd}\end{cases}\end{aligned}$$ The Fourier sine series is in this case: $$f(x)=4\bigl(\sin(x) + \tfrac{1}{3}\sin(3x)+\tfrac{1}{5}\sin(5x)+\tfrac{1}{7}\sin(7x)+\cdots\bigr)$$ In the figure below, the graphs of the square wave and the Fourier sine series with 4 and 16 terms, respectively, have been plotted.

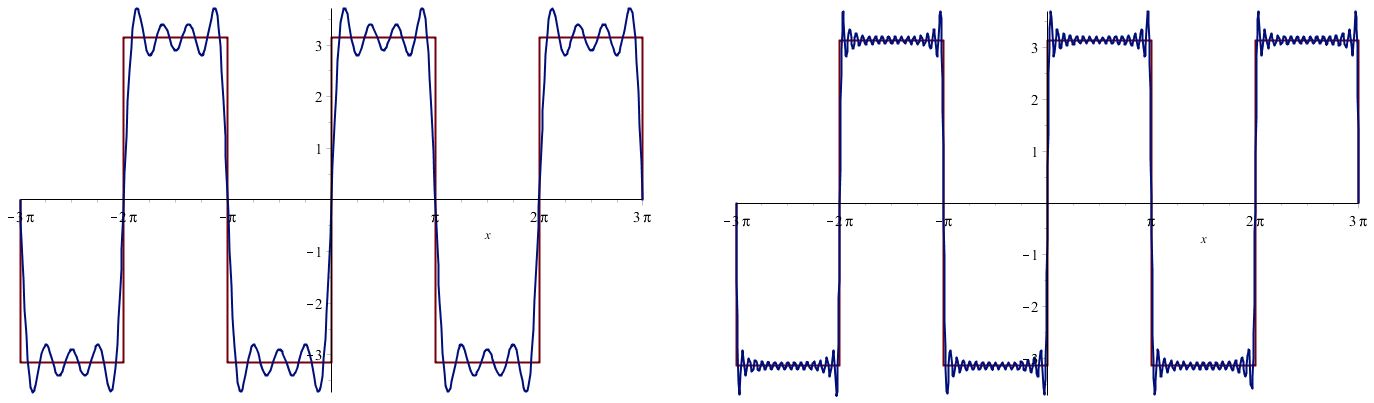
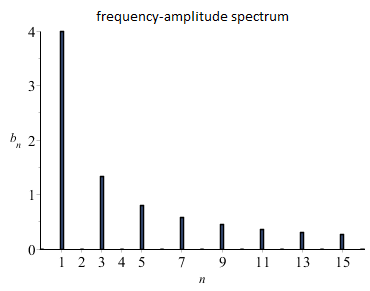
The frequency-amplitude spectrum is shown below: You can see at a glance that the even Fourier sine coefficients are zero and that the frequency levels decrease with increasing $n$.

You can also use the interactive version below to get an impression of how well the function is approximated by a Fourier series and what the frequency-amplitude spectrum looks like.