Functions of several variables: Visualisation of functions of two variables
 Graphs and coordinate curves
Graphs and coordinate curves
The graph of a function \(f\) of one variable is by definition the set of points \((x,y)\) with \(y=f(x)\). Similarly, you can define the graph a function \(f\) of two variables as the set of points \((x,y,z)\) with \(z=f(x,y)\). The graph is a surface in three-dimensional space.
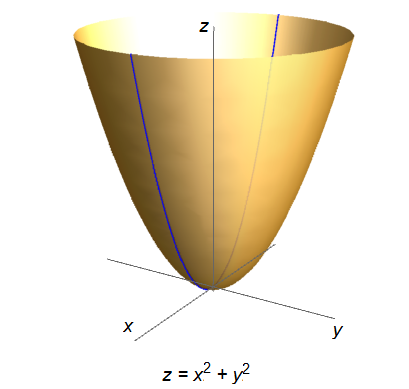
Example 1 The function \(f(x,y)=x^2+y^2\) has a domain in which all values of \(x\) and \(y\) are allowed. A part of the graph has been drawn in the figure below and is a paraboloid that can also be constructed by revolution of the parabola \(z=x^2\) with respect to the \(z\)-axis.
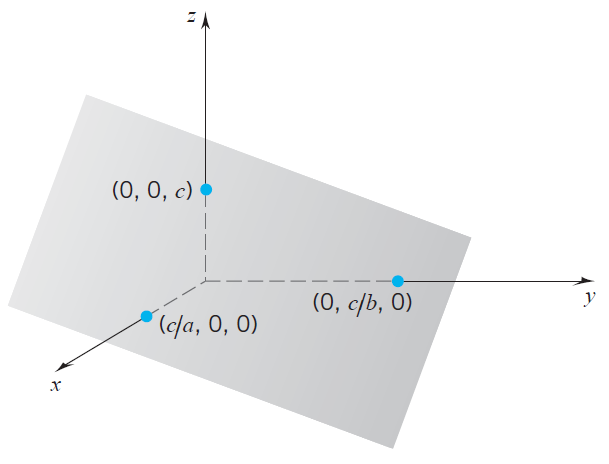
Example 2 The graph of the function \(f(x,y)=c-ax-by\) is a plane through the points \((c/a,0,0)\), \((0,c/b,0)\) and \((0,0,c)\).
When plotting a graph of a function of two variables one often uses besides coordinate axes other means to enlarge the spatial suggestion. For example, one embeds the drawn figure in a box, of which the \(xy\)-plane is equal to the rectangular part of the domain for which points of the surface are drawn. Also one uses in mathematical software colouring of the surface to suggest depth. Often it contains a wireframe formed by curves on the surface where \(x\) or \(y\) is constant; these are called coordinate curves. In the following example, these visualization tricks are deployed.
Example 3 The graph of the function \(f(x,y)=\tfrac{1}{2}\!(1-\sin(2x^2-y-1)\) is a curved surface. In the following figure, the coordinate curves through the point \(P=\bigl(0.3, 0.5, f(0.3, 0.5)\bigr)\) are plotted in a darker colour. One curve corresponds with all points on the surface for which \(x=0.3\) and the other curve corresponds with all points for which \(y=0.5\). The entire wireframe of coordinate curves is drawn for \(x=0.0, 0.1, \ldots , 0.9, 1.0\) and for \(y=0.0, 0.1, \ldots , 0.9, 1.0\). The wireframe and the surrounding cubic box are no part of the graph of \(f\); they are only meant to give a better spatial impression of the surface.
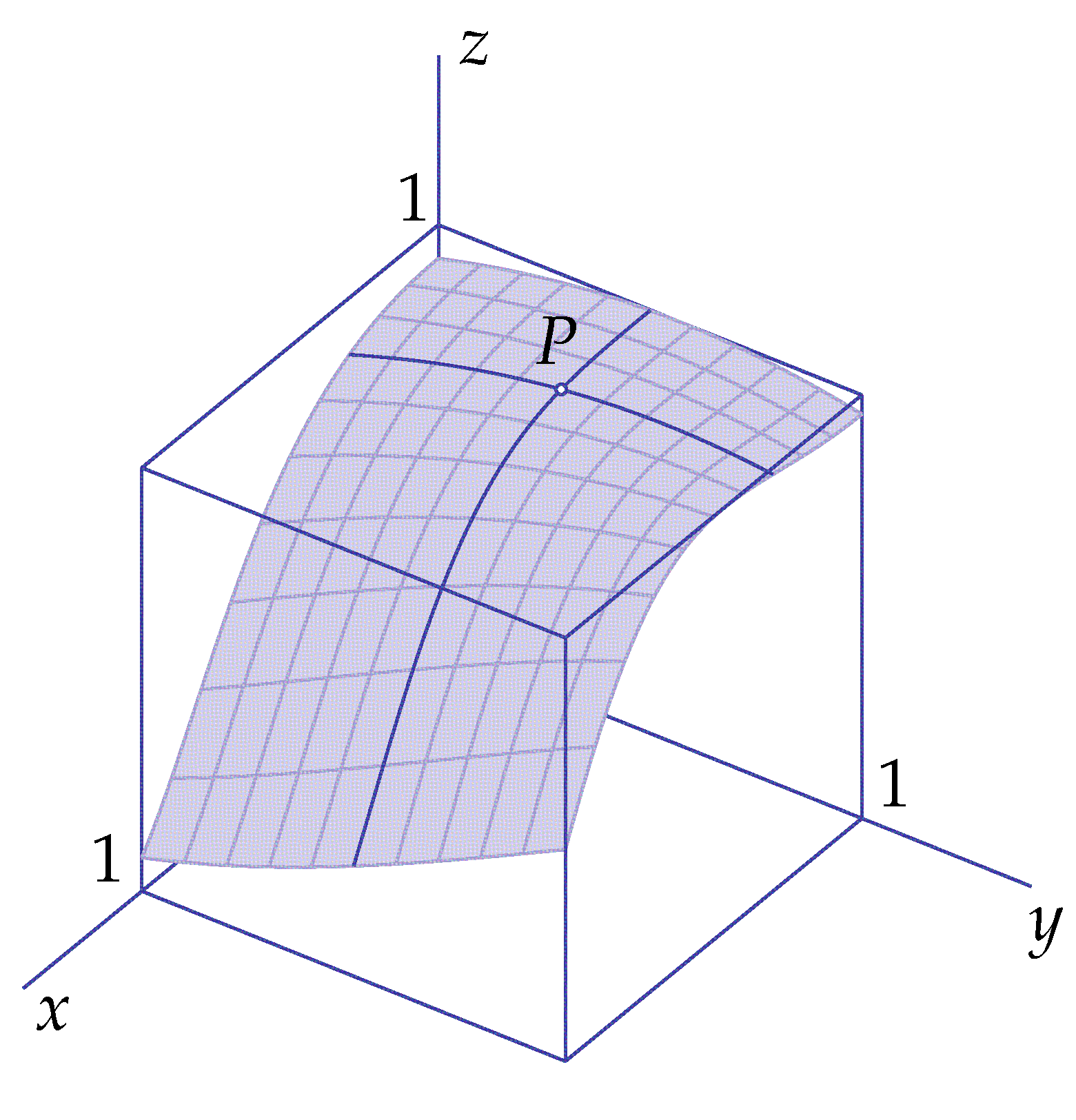
\[z=\tfrac{1}{2}\!(1-\sin(2x^2-y-1)\]


