Functies van meer variabelen: Visualisaties van functies van twee variabelen
 Grafieken en coördinaatkrommen
Grafieken en coördinaatkrommen
De grafiek van een functie \(f\) van één variabele is per definitie de verzameling punten \((x,y)\) met \(y=f(x)\). Op dezelfde manier kun je de grafiek van een functie \(f\) van twee variabelen definiëren als de verzameling punten \((x,y,z)\) met \(z=f(x,y)\). De tekening van de grafiek is een oppervlak in de 3-dimensionale ruimte.
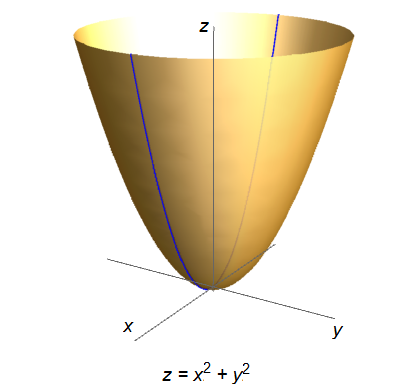
Example 1 De functie \(f(x,y)=x^2+y^2\) heeft een domein waarin alle waarden van \(x\) en \(y\) toegestaan zijn. De grafiek is in onderstaande figuur (voor een stukje) getekend en is een paraboloïde die ook geconstrueerd kan worden door omwenteling van de parabool \(z=x^2\) om de \(z-as\).
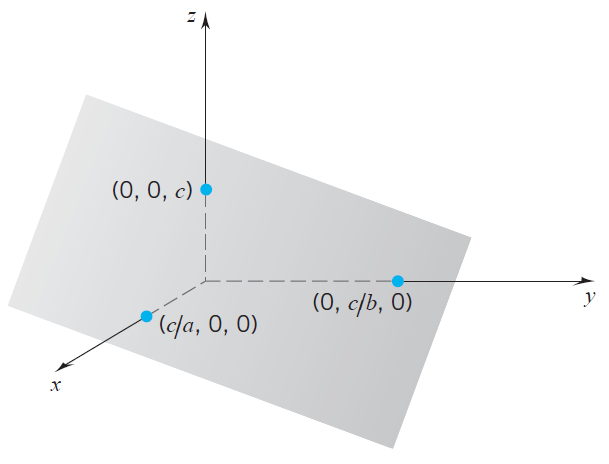
Example 2 De grafiek van de functie \(f(x,y)=c-ax-by\) is een vlak door de punten \((c/a,0,0)\), \((0,c/b,0)\) en \((0,0,c)\).
Bij een tekening van een grafiek van een functie van twee variabelen worden vaak i.p.v. coördinaatassen andere middelen ingezet om de ruimtelijke suggestie te vergroten. Bijvoorbeeld wordt om de figuur een kubus of balk heen getekend waarvan het \(xy\)-vlak gelijk is aan het rechthoekige deel van het domein waarvoor punten van het oppervlak getekend worden. Ook wordt in wiskundige software kleuring van het oppervlak gebruikt om diepte te suggereren. Vaak is tevens het coördinatennet aangegeven, gevormd door lijnen op het oppervlak, waar \(x\), dan wel \(y\) constant is; dit worden coördinaatkrommen genoemd. In onderstaand voorbeeld zijn deze visualisatie trucs toegepast.
Example 3 De grafiek van de functie \(f(x,y)=\tfrac{1}{2}\!(1-\sin(2x^2-y-1)\) is een gekromd oppervlak. In onderstaande tekening zijn de coördinaatkrommen door het punt \(P=\bigl(0.3, 0.5, f(0.3, 0.5)\bigr)\) donkerder getekend. De ene kromme hoort dus bij alle punten op het oppervlak waarvoor geldt dat \(x=0.3\), de andere kromme hoort bij alle punten waarvoor geldt dat \(y=0.5\). Het gehele coördinatennet is getekend voor \(x=0.0, 0.1, \ldots , 0.9, 1.0\) en voor \(y=0.0, 0.1, \ldots , 0.9, 1.0\). Het coördinatennet en de kubus maken dus geen deel uit van de grafiek van \(f\); ze zijn enkel bedoeld om een betere ruimtelijke indruk van het oppervlak te krijgen.
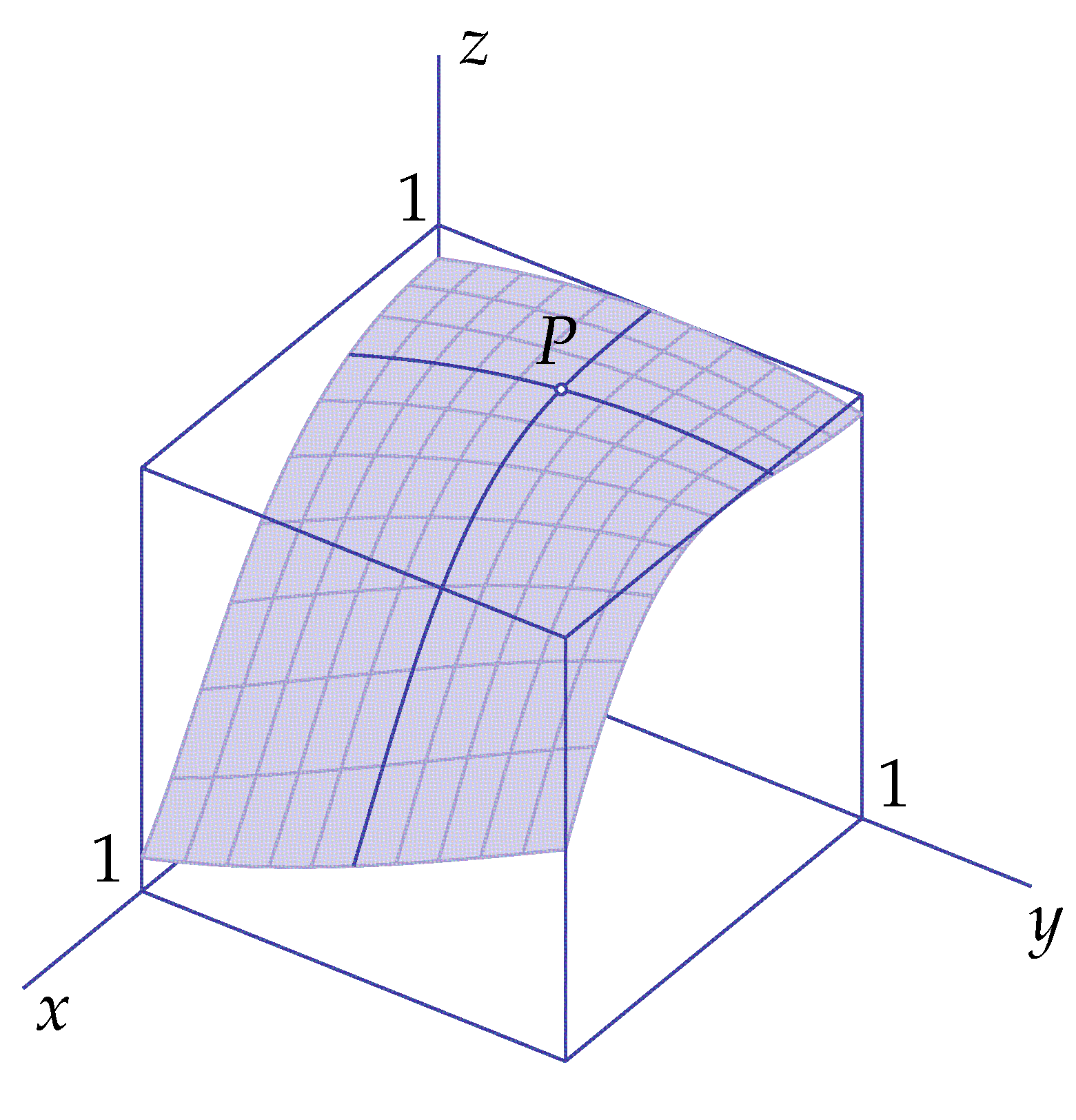
\[z=\tfrac{1}{2}\!(1-\sin(2x^2-y-1)\]


