Functies van meer variabelen: Visualisaties van functies van twee variabelen
 Niveaukrommen en contourgrafieken
Niveaukrommen en contourgrafieken
Om bij weerkaarten een indruk te geven van luchtdrukverschillen en om bij topografische kaarten een indruk te geven van hoogteverschillen worden vaak niveaukrommen gebruikt. Krommen met gelijke luchtdruk heten isobaren. Hoogtelijnen zijn krommen op een kaart die punten van gelijke hoogte met elkaar verbinden. Onderstaande figuur illustreert de constructie van een hoogtekaart, waarbij de hoogtelijnen op de tekening (boven) van het landschap geprojecteerd zijn op een topografische kaart (onder):
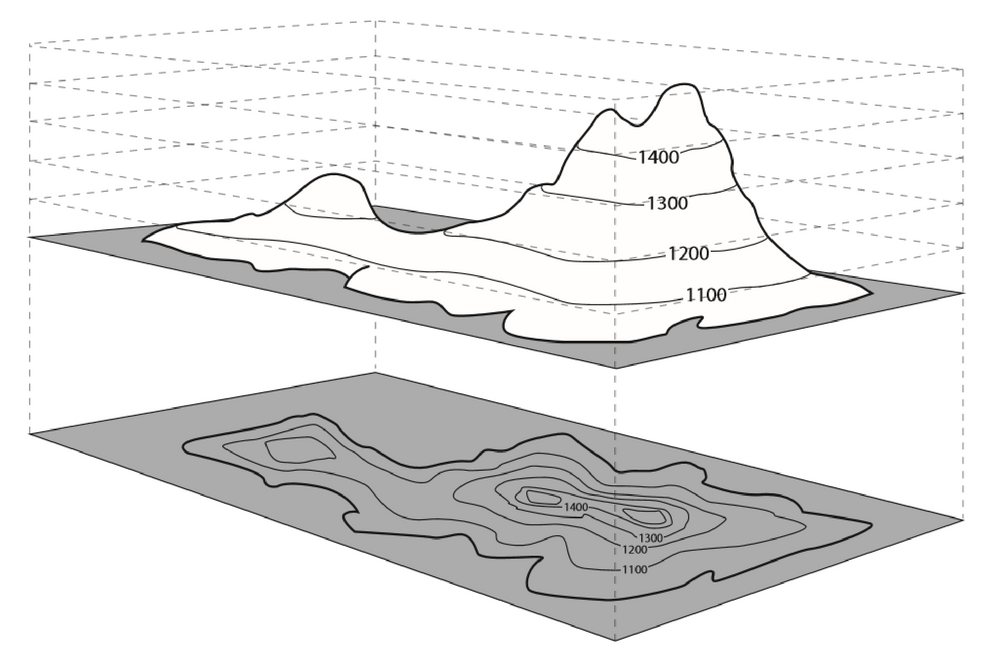
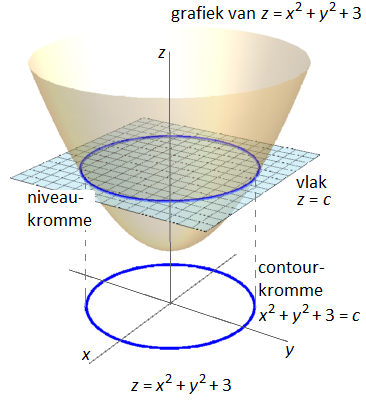
Maar deze constructie zou je ook op oppervlakken van een functie in twee veranderlijken kunnen toepassen. We spreken dan van isolijnen of niveaukrommen. Ze zijn gedefinieerd als krommen in de grafiek van een functie van twee variabelen, zeg \(z=f(x,y)\), met constante functiewaarden. Met ander woorden, het zijn punten op het oppervlak waar de functie hetzelfde niveau heeft. Op zo'n kromme is \(z=f(x,y)\) dus constant. De projectie op het \(xy\)-vlak heet een contourkromme Hieronder zie je hoe een contourkromme van de voorbeeldfunctie \(f(x,y)=x^2+y^2+3\) geconstrueerd wordt.
We geven een paar voorbeelden.
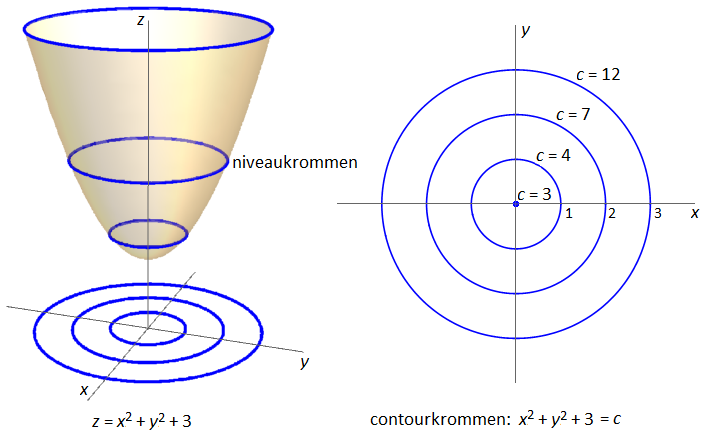
Voorbeeld 1 Aan de linkerkant van onderstaande figuur zijn de grafiek van de functie \(f(x,y)=x^2+y^2+3\) samen met niveaukrommen getekend en aan de rechterkant staan de bijpassende contourkrommen (bij \(c=3\) is dat een punt); samen vormen contourkrommen de contourgrafiek van de functie \(f(x,y)\).
De volgende interactieve versie kan je inzicht in de constructie van contourgrafieken vergroten.
Voorbeeld 2 De contourgrafiek van de functie \(f(x,y)=4-4x-4y\) bestaat uit parallelle lijnen.
Visualisatie software staat vaak ook toe niveaukrommen op het oppervlak van een functie van twee variabelen te tonen.
Voorbeeld 3 In onderstaande grafiek van de functie \(f(x,y)=\tfrac{1}{2}(1-\sin(2x^2-y-1)\) zijn de niveaukrommen op het oppervlak getekend voor \(z=1.00, z=0.95, z=0.90, \ldots\).
Laten we de projectie van één van de niveaukrommen op het \(xy\)-vlak eens in detail bekijken, namelijk de niveaukromme met waarde \(1\). Dan moet gelden \[\tfrac{1}{2}(1-\sin(2x^2-y-1)=1\]. Dit geeft na omwerken de vergelijking \[\sin(2x^2-y-1)=1\] Binnen het gekozen coördinatenstelsel geldt dan \[2x^2-y-1=-\tfrac{1}{2}\pi\] oftewel \[y = 2x^2+\tfrac{1}{2}\pi-1\] De contourkromme is dus een parabool.


