In the figure below, tangent vectors at the point $P=(a,b,c)$ with $c=f(a,b)$ are drawn along the coordinate curves through that point: the point $P$ is the initial point of both vectors. One tangent vector has a component in the $x$ direction , which we name $\dd x$, and a component in the $y$ direction which is equal to zero. The component $\dd z$ in the $z$ direction is equal to $f_x(a,b)\,\dd x$ because we have the function $z=f(x,b)$ of one variable on the coordinate curve, and so we can specify the differential. The tangent vector starting at point $P=(a,b)$ is

$$\left(\begin{array}{c} \dd x \\ 0 \\ \dd z\end{array}\right)=\left(\begin{array}{c} \dd x \\ 0 \\ f_x(a,b)\,\dd x\end{array}\right)=\mathbf{r}\,\dd x\quad\text{with}\quad \mathbf{r}=\left(\begin{array}{c} 1 \\ 0 \\ f_x(a,b)\end{array}\right)$$ The other tangent vector has a component in the $y$ direction, which we name $\dd y$, and a component in the $x$ direction that is equal to zero. The component $dz$ in the $z$ direction is equal to $f_y(a,b)\,\dd y$ because we have the function $z=f(a,y)$ of one variable on the coordinate curve, and so we can specify the differential. If the graph of $f(x,y)$ is a smooth surface near the point $P=\bigl(a,b,f(a,b)\bigr)$, then the tangent vector starting at point $P$ is $$\left(\begin{array}{c} 0 \\ \dd y \\ \dd z\end{array}\right)=\left(\begin{array}{c} 0 \\ \dd y \\ f_y(a,b)\,\dd y\end{array}\right)=\mathbf{s}\,\dd y\quad\text{with}\quad \mathbf{s}=\left(\begin{array}{c} 0 \\ 1 \\ f_y(a,b)\end{array}\right)$$

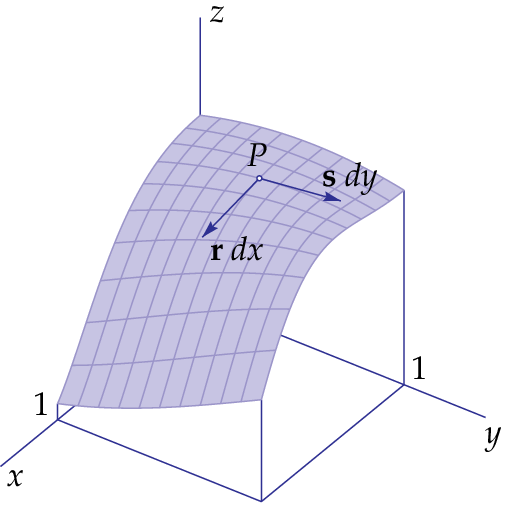
In the figure above, we have chosen components $\dd x$ and $\dd y$ of size $0.4$, but you might as well make such a choice that the length of both tangent vectors is equal to one. The tangent vectors $\mathbf{r}$ and $\mathbf{s}$ span the tangent plane of the graph of $f(x,y)$ at the point $P$. Each vector with initial point $P$ in the tangent plane is a linear combination $\lambda\,\mathbf{r}+\mu\,\mathbf{s}$ of $\mathbf{r}$ and $\mathbf{s}$. Each of these vectors is a tangent vector at the point $P$ on the surface plot of $f(x,y)$. The following figure visualizes this.

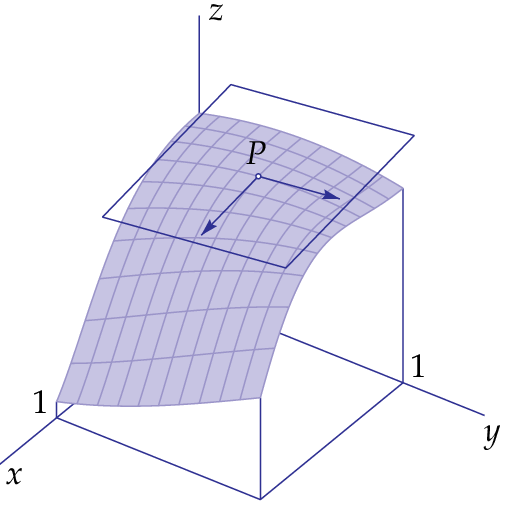
For the vector representation of the tangent plane at point $P$ we may use the vector with the origin as initial point and $P$ terminal point as support vector.