In onderstaande figuur zijn raakvectoren aan de coördinaatlijnen door het punt \(P=(a,b,c)\) met \(c=f(a,b)\) getekend: ze hebben beide het punt \(P\) als aangrijpingspunt. De ene raakvector heeft een component in de \(x\)-richting die we \(\dd x\) noemen en een component in de \(y\)-richting die gelijk aan nul is. De component \(\dd z\) in de \(z\)-richting is dan gelijk aan \(f_x(a,b)\,\dd x\) want langs de coördinaatlijn hebben we de functie \(z=f(x,b)\) in één veranderlijke en hiervoor kunnen we de differentiaal opschrijven. De raakvector startend in het punt \(P=(a,b)\) is dus \[\left(\begin{array}{c} \dd x \\ 0 \\ \dd z\end{array}\right)=\left(\begin{array}{c} \dd x \\ 0 \\ f_x(a,b)\,\dd x\end{array}\right)=\mathbf{r}\,\dd x\quad\text{met}\quad \mathbf{r}=\left(\begin{array}{c} 1 \\ 0 \\ f_x(a,b)\end{array}\right)\] De andere raakvector heeft een een component in de \(y\)-richting die we \(\dd y\) noemen en een component in de \(x\)-richting die gelijk aan nul is. De component \(\dd z\) in de \(z\)-richting is dan gelijk aan \(f_y(a,b)\,\dd y\) want langs de coördinaatlijn hebben we de functie \(z=f(a,y)\) in één veranderlijke en hiervoor kunnen we de differentiaal opschrijven. Als de grafiek van \(f\) een glad oppervlak is in de buurt van het punt\(P=\bigl(a,b,f(a,b)\bigr)\), dan is de raakvector startend in het punt \(P=(a,b)\) dus \[\left(\begin{array}{c} 0 \\ \dd y \\ \dd z\end{array}\right)=\left(\begin{array}{c} 0 \\ \dd y \\ f_y(a,b)\,\dd y\end{array}\right)=\mathbf{s}\,\dd y\quad\text{met}\quad \mathbf{s}=\left(\begin{array}{c} 0 \\ 1 \\ f_y(a,b)\end{array}\right)\]

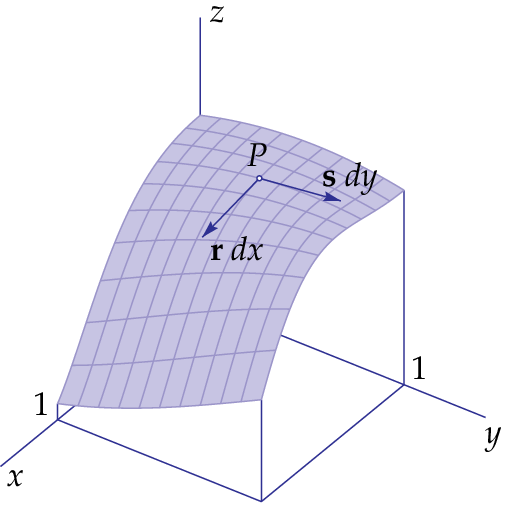
In het getekende voorbeeld hebben we \(\dd x=\dd y=0.4\) genomen, maar je kunt net zo goed een dusdanige keuze maken dat de norm van de raakvectoren gelijk aan 1 is. De raakvectoren \(\mathbf{r}\) en \(\mathbf{s}\) spannen het raakvlak aan de grafiek van \(f(x,y)\) in het punt \(P\) op. Elke vector met aangrijpingspunt \(P\) in het raakvlak is een lineaire combinatie \(\lambda\,\mathbf{r}+\mu\,\mathbf{s}\) van \(\mathbf{r}\) en \(\mathbf{s}\) en zo'n vector is een raakvector in \(P\) aan het oppervlak dat de grafiek van \(f(x,y)\) vormt. Onderstaande figuur visualiseert dit.

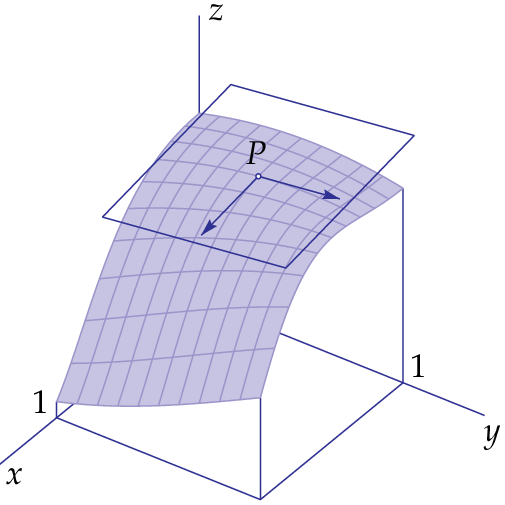
Voor de vectorvoorstelling van het raakvlak in punt \(P\) mogen de vector met de oorsprong als aangrijpingspunt en eindpunt in \(P\) als steunvector nemen.