Functions of several variables: Tangent vector and tangent plane
 An equation of a tangent plane
An equation of a tangent plane
Interlude: an equation of a plane We will determine an equation of a tangent plane. This requires that you know how to determine an equation of an arbitrary plane in a three-dimensional space when you know two direction vectors of the plane. In general, the equation of a plane is of the from \[ax+by+cz+d=0\] with \(a,b,c\) numbers that are not all equal to \(0\), and a fourth number \(d\). Note that the numbers \(a\), \(b\), \(c\) and \(d\) are not unique: each multiple of the quartet describes the same plane in the three-dimensional space. So we should really speak of an equation of a plane. The plane with equation \(ax+by+cz+d=0\) is parallel to the plane through the origin given by the equation \[ax+by+cz=0\] This equation can also be written as inner product of two vectors, namely, \[\left(\begin{array}{c} a \\ b \\ c\end{array}\right)\mathbf{\cdot} \left(\begin{array}{c} x\\ y\\ z\end{array}\right) = 0\] In other words, the vector starting at the origin and ending at \((x,y,z)\) points toward a point on the plane through the origin if the vector is perpendicular to the vector with components \(a\), \(b\) and \(c\). In other words, the vector \(\left(\begin{array}{c} a \\ b \\ c\end{array} \right) \) is orthogonal to any vector in the plane. This is a normal vector of the plane. Given two vectors \(\mathbf {a} = \left( \begin{array}{c}a_1 \\ a_2 \\ a_3\end {array} \right) \), and \(\mathbf{b} = \left(\begin{array}{c}b_1 \\ b_2 \\ b_3\end {array} \right) \) that do not lie in line with each other in a plane through the origin, an admissible normal vector is the cross product \(\mathbf{a}\times \mathbf{b}\) of \(\mathbf{a}\) and \(\mathbf{b}\)(in this order!), defined as \[\mathbf{a}\times \mathbf{b}=\left(\begin{array}{c} a_2b_3-a_3b_2 \\ a_3b_1-a_1b_3 \\ a_1b_2-a_2b_1 \end{array}\right)\]
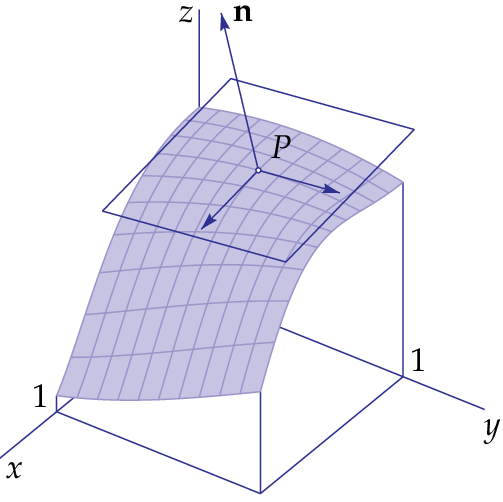
After the above interlude we return to the subject of functions of two variables: let \(z=f(x,y)\) be a function of two variables \(x\) and \(y\). We consider a point \(P=(a,b,c)\) with \(c=f(a,b)\) and assume that the graph of \(f\) is a smooth surface near point \(P\). We know that the vectors \[\mathbf{r}=\left(\begin{array}{c} 1 \\ 0 \\ f_x(a,b)\end{array}\right)\quad \text{and}\quad \mathbf{s}=\left(\begin{array}{c} 0 \\ 1 \\ f_y(a,b)\end{array}\right)\] span the tangent plane at \(P\). To find an equation of the tangent plane it is sufficient to find a normal vector of this plane. This can be done via the cross product of \(\mathbf{r}\) and \(\mathbf{s}\): \[\mathbf{n}=\mathbf{r}\times \mathbf{s}= \left(\begin{array}{c} -f_x(a,b) \\ -f_y(a,b) \\ 1\end{array}\right)\] In this way we find the following equation of the tangent plane.
An equation of a tangent plane An equation of the tangent plane at the point \(P=(a,b,c)\) with \(c=f(a,b)\) is \[-f_x(a,b)(x-a)-f_y(a,b)(y-b)+(z-c)=0\] and thus \[z=f(a,b) + f_x(a,b)(x-a)+f_y(a,b)(y-b)\]