Functions of several variables: Total differential and Taylor approximation
 The total differential
The total differential
Let \(z=f(x,y)\) be a neat function of two variables \(x\) and \(y\). We consider a point \(P=(a,b,c)\) with \(c=f(a,b)\). We know that the vectors \[\mathbf{r}=\left(\begin{array}{c} 1 \\ 0 \\ f_x(a,b)\end{array}\right)\quad \text{and}\quad \mathbf{s}=\left(\begin{array}{c} 0 \\ 1 \\ f_y(a,b)\end{array}\right)\] span the tangent plane. An arbitrary tangent vector \(\mathbf t\) at a point \(P\) on the graph of \(f(x,y)\) is a linear combination of these vectors, say of the form \[\begin{aligned}\mathbf{t} &= \mathbf{r}\,\dd x+\mathbf{s}\,\dd y\\ \\ &=\left(\begin{array}{c} \dd x \\ 0 \\ f_x(a,b)\,\dd x\end{array}\right)+\left(\begin{array}{c} 0 \\ \dd y \\ f_y(a,b)\,\dd y\end{array}\right)\\ \\ &=\left(\begin{array}{c} \dd x \\ \dd y \\ f_x(a,b)\,\dd x+f_y(a,b)\,\dd y\end{array}\right)\end{aligned}\]
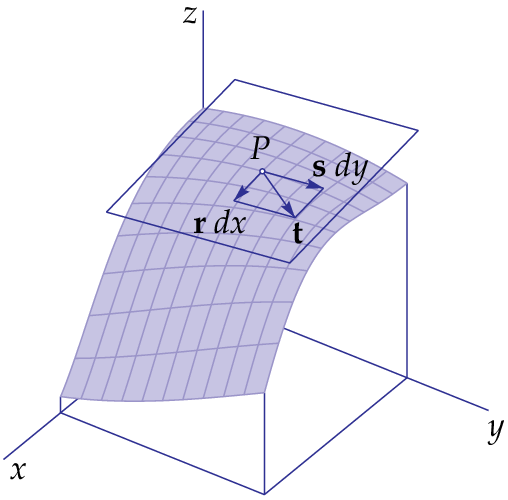
The first component, \(\dd x\), is the increase of the \(x\) coordinate along \(\mathbf{t}\), the second component, \(\dd y\), is the increase \(y\) coordinate along \(\mathbf{t}\), and the third component is the increase in the \(z\) coordinate along \(\mathbf{t}\). For very small \(\dd x\) and \(\dd y\), the tangent plane at \(P\) practically coincides with the graph of \(f(x,y)\) near that point, and the increase in \(z\) thus virtually coincides with the increase in \(f(x,y)\). This increase of \(f(x,y)\), denoted as \({\vartriangle}f\), is given by \[{\vartriangle}f=f(a+\dd x,b+\dd y)-f(a,b)\] and for very small \(\dd x\) and \(\dd y\) almost equal to \[f_x(a,b)\,\dd x+f_y(a,b)\,\dd y\] The last expression is called the total differential of \(f(x,y)\) at the point \(P=(a,b)\). The notation for the total differential is \(\dd\bigl(f(a,b)\bigr)\), but as with functions of one variable, we leave in the notation out the dependency of the differential of the chosen point \(P\) and we write the following:
Definition The total differential of the function \(f(x,y)\) of two variables \(x\) and \(y\) is denoted by \(\dd f\) and is defined by the following formula: \[\dd f=f_x\,\dd x+f_y\,\dd y\qquad \text{that is}\qquad \dd f=\frac{\partial f}{\partial x}\dd x +\frac{\partial f}{\partial y}\,\dd y\]
In the figure above, the function is once more \(f(x,y)=\tfrac{1}{2}\bigl(1-\sin(2x^2-y-1)\bigr)\) and we have selected the point \(P=(0.3,0.5)\). For the clarity of the figure, the increase \(\dd x=0.2, \dd y=0.3\) have not been chosen too small and the deviation between the tangent plane and the graph of \(f\) is not small: the difference between the total differential \(\dd f\) at \(P\) and the function value difference \({\vartriangle}f\) is about \(0.01\). But when we choose our \(\dd x\) and \(\dd y\) ten times smaller ( \(\dd x=0.02\) and \(\dd y=0.03\) ), then the total differential \(\dd f\) at \(P\) equals \[\dd f=f_x(0.3,0.5)\,\dd x+ f_y(0.3,0.5)\,\dd y\approx -0.14891\times 0.02 + -0.12409\times 0.03\approx 0.00074\] while the function value difference \({\vartriangle}f\) in this case equals \[{\vartriangle}f= f(0.32, 0.53)-f(0.3,0.5)\approx 0.00064\] The difference between \(df\) and \({\vartriangle}f\) is only \(0.0001\). When we make \(\dd x\) and \(\dd y\) another ten times smaller, the difference is about \(0.000001\)!
We consider the function \(z=z(x,y)=\frac{x}{y}\). The total differential \(dz\) is then given by \[\begin{aligned} \dd z &=\frac{\partial f}{\partial x}\,\dd x+\frac{\partial f}{\partial y}\,\dd y \\ \\ &= \frac{1}{y}\dd x-\frac{x}{y^2}\,\dd y\end{aligned}\]
The total differential can be defined in a similar way for functions of three or more variables; for instance
Definition The total differential of the function \(f(x,y,z)\) of three variables \(x\), \(y\) and \(z\) is denoted by \(df\) and is defined by the following formula: \[\dd f=f_x\,\dd x+f_y\,\dd y+f_z\,\dd z\qquad \text{that is}\qquad \dd f=\frac{\partial f}{\partial x}\,\dd x+\frac{\partial f}{\partial y}\,\dd y+\frac{\partial f}{\partial z}\,\dd z\]


