Stel \(z=f(x,y)\) is een 'nette' functie van twee variabelen \(x\) en \(y\). We bekijken een punt \(P=(a,b,c)\) met \(c=f(a,b)\). We weten dat de vectoren \[\mathbf{r}=\left(\begin{array}{c} 1 \\ 0 \\ f_x(a,b)\end{array}\right)\quad \text{en}\quad \mathbf{s}=\left(\begin{array}{c} 0 \\ 1 \\ f_y(a,b)\end{array}\right)\] het raakvlak opspannen. Een willekeurige raakvector \(\mathbf t\) aan de grafiek van \(f(x,y)\) in \(P\) is een lineaire combinatie van bovenstaande vectoren, zeg van de vorm \[\begin{aligned}\mathbf{t} &= \mathbf{r}\,\dd x+\mathbf{s}\,\dd y\\ \\ &=\left(\begin{array}{c} dx \\ 0 \\ f_x(a,b)\,\dd x\end{array}\right)+\left(\begin{array}{c} 0 \\ \dd y \\ f_y(a,b)\,dy\end{array}\right)\\ \\ &=\left(\begin{array}{c} \dd x \\ \dd y \\ f_x(a,b)\,\dd x+f_y(a,b)\,\dd y\end{array}\right)\end{aligned}\]

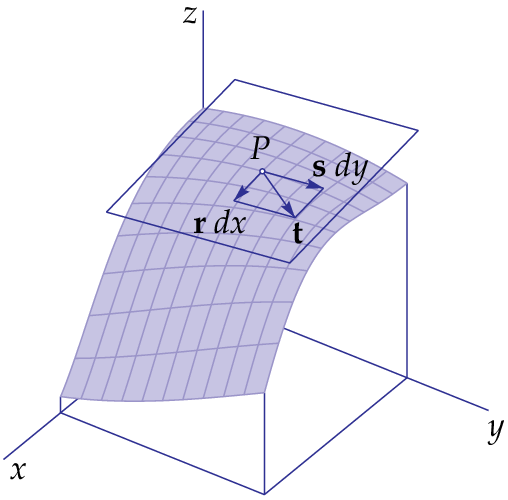
De eerste component, \(\dd x\), is de toename van de \(x\)-coördinaat langs \(\mathbf{t}\), de tweede component, \(\dd y\), is de toename van de \(y\)-coördinaat langs \(\mathbf{t}\) en de derde component is de toename van de \(z\)-coördinaat langs \(\mathbf{t}\). Voor zeer kleine \(\dd x\) en \(\dd y\) valt het raakvlak in \(P\) vrijwel samen met de grafiek van \(f(x,y)\) nabij dit punt, en de toename van \(z\) valt dus vrijwel samen met de toename van \(f(x,y)\). Die toename van \(f(x,y)\), genoteerd als \({\vartriangle}f\), wordt gegeven door \[{\vartriangle}f=f(a+\dd x,b+\dd y)-f(a,b)\] en is voor zeer kleine \(\dd x\) en \(\dd y\) vrijwel gelijk aan \[f_x(a,b)\,\dd x+f_y(a,b)\,\dd y\] De laatste uitdrukking heet de totale differentiaal van \(f(x,y)\) in het punt \(P=(a,b)\) bij infinitesimale \(\dd x\) en \(\dd y\). De notatie voor de totale differentiaal is \(\dd\bigl(f(a,b)\bigr)\), maar net als bij functies van één veranderlijke laten we in de notatie de afhankelijkheid van de differentiaal van het gekozen punt \(P\) achterwege en schrijven we het volgende:

In bovenstaande tekening is, net als eerder, de functie \(f(x,y)=\tfrac{1}{2}\bigl(1-\sin(2x^2-y-1)\bigr)\) en het punt \(P=(0.3,0.5)\) genomen. Voor de duidelijkheid van het plaatje zijn de toenames \(\dd x=0.2, \dd y=0.3\) niet al te klein gekozen en is de afwijking tussen raakvlak en grafiek niet zo heel klein: het verschil tussen de totale differentiaal \(\dd f\) in \(P\) en het functiewaardenverschil \({\vartriangle}f\) is hierbij ongeveer \(0.01\). Maar kies je \(\dd x\) en \(\dd y\) tien keer zo klein (\(dx=0.02\) en \(dy=0.03\)), dan is de totale differentiaal \(\dd f\) in \(P\) gelijk aan \[\dd f=f_x(0.3,0.5)\,\dd x+ f_y(0.3,0.5)\,\dd y\approx -0.14891\times 0.02 + -0.12409\times 0.03\approx 0.00074\] terwijl het functiewaardenverschil \({\vartriangle}f\) in dit geval gelijk is aan \[{\vartriangle}f= f(0.32, 0.53)-f(0.3,0.5)\approx 0.00064\] Het verschil tussen \(\dd f\) en \({\vartriangle}f\) is nog maar \(0.0001\). Maak je \(\dd x\) en \(\dd y\) nog eens tien keer zo klein, dan blijkt het verschil ongeveer \(0.000001\) te zijn!

Voor functies van drie of meer variabelen wordt op soortgelijke manier de totale differentiaal gedefinieerd; bijvoorbeeld