Functions of several variables: Total differential and Taylor approximation
 Taylor approximations
Taylor approximations
For a neat function \(f(x)\) of one variable we have already seen that we can approximate the graph of the function near a point \(x=a\) by the tangent line at this point defined by the equation \[y=f(a)+f'(a)\cdot (x-a)\tiny.\] For functions of two variables, we can define a similar linear approximation (also referred to as first-order approximation) near a point; in this case we use the tangent plane at the selected point on the graph of the given function.
Linear approximation For a neat function \(f(x,y)\) of two variables \(x\) and \(y\) we can approximate function values near the point \((x,y)=(a,b)\) via the tangent plane at this point defined by the equation \[z=f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b)\tiny.\]
For functions \(f(x)\) of one variable we have already seen that the linear approximation was the same as the Taylor polynomial of degree 1, and that we get more precise approximations when we consider a Taylor polynomial of higher degree, for example, the following quadratic approximation (second order approximation): \[f(x)\approx f(a)+f'(a)(x-a)+\tfrac{1}{2}f''(a)(x-a)^2\] For functions of two variables we can define a similar approximation of second order:
Quadratic approximation For a neat function \(f(x,y)\) of two variables \(x\) and \(y\) we can approximate function values near the point \((x,y)=(a,b)\)via \[\begin{aligned}f(x,y) &\approx f(a,b)+f_x(a,b){\vartriangle}x+f_y(a,b){\vartriangle}y\\ &\phantom{=}+ \frac{1}{2}\left(f_{xx}(a,b){\vartriangle}x^2+2f_{xy}(a,b){\vartriangle}x{\vartriangle}y+f_{yy}(a,b){\vartriangle}y^2\right)\end{aligned}\] with \[{\vartriangle}x=x-a\quad\text{and}\quad {\vartriangle}y=y-b\tiny.\]
We calculate the quadratic approximation at the point \((1,1)\) for the function \[f(x,y)=x^2y-xy^2-3xy\tiny.\] The graph of the function is as follows:
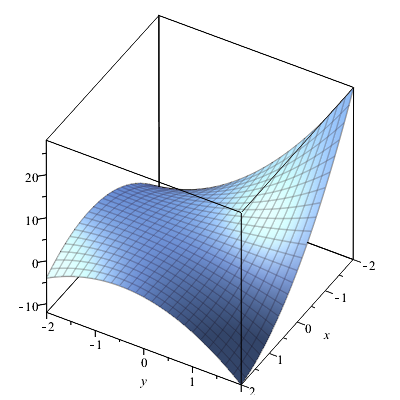
The required partial derivatives are \[f_x(x,y)=2xy-y^2-3y,\quad f_y(x,y)=x^2-2xy-3x,\] \[f_{xx}(x,y)=2y,\quad f_{xy}(x,y)=2x-2y-3\quad\text{en}\quad f_{yy}(x,y)=-2x\tiny.\] Substitution of the coordinates of the point \((1,1)\) in the partial derivatives and in the general formula for the quadratic approximation gives \[\begin{aligned}z(x,y) &= -3-2(x-1)-4(y-1)+(x-1)^2-3(x-1)(y-1)-(y-1)^2\\ \\ &= -x+y + x^2-3xy-y^2\end{aligned}\] The graph of this approximation looks as follows:
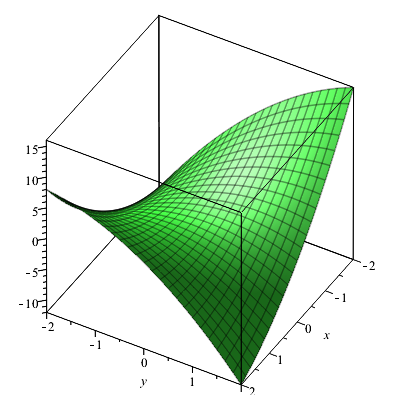
Together in one figure we get:
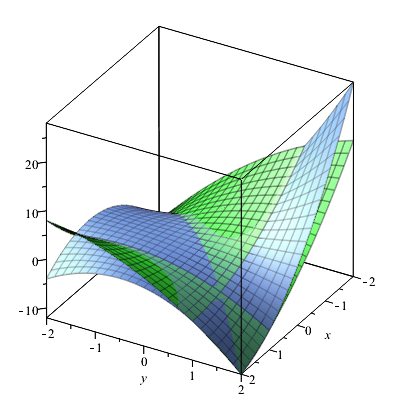
The function and the Taylor approximation do not differ much near \((1,1)\); further away though, they are substantially different.
The linear and quadratic approximations of functions of two variables originate from the Taylor's theorem of first and second order.
Taylor's theorem of first order For a neat function \(f(x,y)\) of two variables \(x\) and \(y\), the following statement is true near the point \((x,y)=(a,b)\) with \( {\vartriangle} x=x-a\) and \({\vartriangle}y=y-b\): \[ f(x,y) = f(a,b)+f_x(a,b){\vartriangle}x+f_y(a,b){\vartriangle}y+R_1(x,y)\] with the remainder term \(R_1(x,y)\) given as \[R_1(x,y)=\frac{1}{2!}\left(f_{xx}(\xi,\eta){\vartriangle}x^2+2f_{xy}(\xi,\eta){\vartriangle}x{\vartriangle}y+f_{yy}(\xi,\eta){\vartriangle}y^2\right)\] for some \(\xi\) between \(a\) and \(x\), and some \(\eta\) between \(b\) and \(y\).
Taylor's theorem of second order For a neat function \(f(x,y)\) of two variables \(x\) and \(y\), the following statement is true near the point \((x,y)=(a,b)\) with \({\vartriangle}x=x-a\) and \({\vartriangle}y=y-b\): \[\begin{aligned}f(x,y) &= f(a,b)\\ &\phantom{=}+f_x(a,b){\vartriangle}x+f_y(a,b){\vartriangle}y\\ &\phantom{=}+ \frac{1}{2!}\left(f_{xx}(a,b){\vartriangle}x^2+2f_{xy}(a,b){\vartriangle}x{\vartriangle}y+f_{yy}(a,b){\vartriangle}y^2\right)+R_2(x,y)\end{aligned}\] with the remainder term \(R_2(x,y)\) given as \[\begin{aligned}R_2(x,y) &= \frac{1}{3!}\Bigl(f_{xxx}(\xi,\eta){\vartriangle}x^3+3f_{xxy}(\xi,\eta){\vartriangle}x^2{\vartriangle}y\\ &\phantom{=xxx} +3f_{xyy}(\xi,\eta){\vartriangle}x{\vartriangle}y^2 +f_{yyy}(\xi,\eta){\vartriangle}y^3\Bigr)\end{aligned}\] for some \(\xi\) between \(a\) and \(x\), and some \(\eta\) between \(b\) and \(y\).
We could continue in this way, but we stop here. The Taylor series of of two variables \(x\) and \(y\) is defined as follows:
Taylor series For a neat function \(f(x,y)\) of two variables \(x\) and \(y\), one can approximate function values near the point \((x,y)=(a,b)\) with \[\begin{aligned}f(x,y) &= f(a,b)\\ &\phantom{=}+f_x(a,b){\vartriangle}x+f_y(a,b){\vartriangle}y\\ &\phantom{=}+ \frac{1}{2!}\left(f_{xx}(a,b){\vartriangle}x^2+2f_{xy}(a,b){\vartriangle}x{\vartriangle}y+f_{yy}(a,b){\vartriangle}y^2\right)\\ &\phantom{=}+ \frac{1}{3!}\Bigl(f_{xxx}(a,b){\vartriangle}x^3+3f_{xxy}(a,b){\vartriangle}x^2{\vartriangle}y\\ &\phantom{=xxxxx}+3f_{xyy}(a,b){\vartriangle}x{\vartriangle}y^2+f_{yyy}(a,b){\vartriangle}y^3\Bigl)\\ &\phantom{=}+\cdots\end{aligned}\] with \[{\vartriangle}x=x-a\quad\text{and}\quad {\vartriangle}y=y-b\tiny.\]


