Functies van meer variabelen: Totale differentiaal en Taylorbenaderingen
 Taylorbenaderingen
Taylorbenaderingen
Bij een 'nette' functie \(f(x)\) van één veranderlijke hebben we al gezien dat we deze rondom een punt \(x=a\) kunnen benaderen met de raaklijn in dit punt gegeven door de vergelijking \[y=f(a)+f'(a)\cdot (x-a)\tiny.\] Voor functies van twee variabelen kunnen we net zo'n lineaire benadering (ook wel eerste orde benadering genoemd) rondom een punt toepassen; in dit geval gebruiken we het raakvlak in het gekozen punt aan de grafiek van de gegeven functie.
Lineaire benadering Bij een 'nette' functie \(f(x,y)\) van twee variabelen \(x\) en \(y\) kunnen we functiewaarden rondom het punt \((x,y)=(a,b)\) benaderen via het raakvlak in dit punt gegeven door de vergelijking \[z=f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b)\tiny.\]
Bij functies \(f(x)\) van één veranderlijke hebben we al gezien dat de lineaire benadering hetzelfde was als de Taylorveelterm van graad 1 en dat we preciezere benaderingen krijgen als we een Taylorveelterm van hogere graad nemen, bijvoorbeeld de volgende kwadratische benadering (tweede orde benadering): \[f(x)\approx f(a)+f'(a)(x-a)+\tfrac{1}{2}f''(a)(x-a)^2\] Voor functies van twee variabelen kunnen we net zo'n benadering van tweede orde nemen:
Kwadratische benadering Bij een 'nette' functie \(f(x,y)\) van twee variabelen \(x\) en \(y\) kunnen we functiewaarden rondom het punt \((x,y)=(a,b)\) benaderen via \[\begin{aligned}f(x,y) &\approx f(a,b)+f_x(a,b){\vartriangle}x+f_y(a,b){\vartriangle}y\\ &\phantom{=}+ \frac{1}{2}\left(f_{xx}(a,b){\vartriangle}x^2+2f_{xy}(a,b){\vartriangle}x{\vartriangle}y+f_{yy}(a,b){\vartriangle}y^2\right)\end{aligned}\] met \[{\vartriangle}x=x-a\quad\text{en}\quad {\vartriangle}y=y-b\tiny.\]
We berekenen de kwadratische benadering rondom het punt \((1,1)\) van de functie \[f(x,y)=x^2y-xy^2-3xy\tiny.\] De grafiek van de functie is
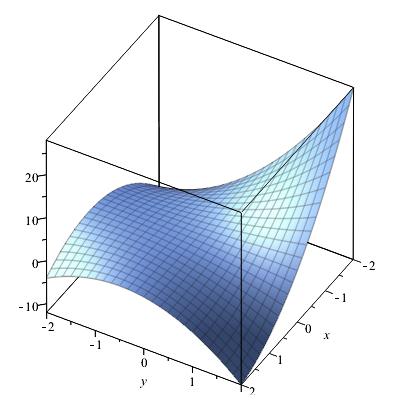
De benodigde partiële afgeleiden zijn \[f_x(x,y)=2xy-y^2-3y,\quad f_y(x,y)=x^2-2xy-3x,\] \[f_{xx}(x,y)=2y,\quad f_{xy}(x,y)=2x-2y-3\quad\text{en}\quad f_{yy}(x,y)=-2x\tiny.\] Invullen van de coördinaten van het punt \((1,1)\) in de partiële afgeleiden en in de algemene formule voor de kwadratische benadering geeft \[\begin{aligned}z(x,y) &= -3-2(x-1)-4(y-1)+(x-1)^2-3(x-1)(y-1)-(y-1)^2\\ \\ &= -x+y + x^2-3xy-y^2\end{aligned}\] De grafiek van deze benadering is
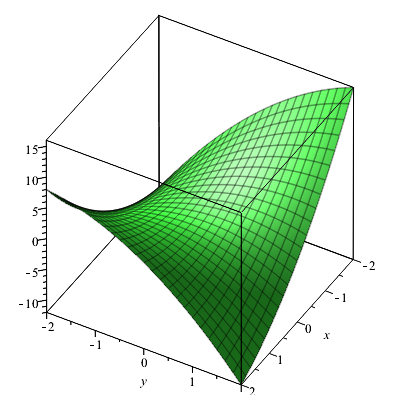
Samen in één figuur ziet het er uit als
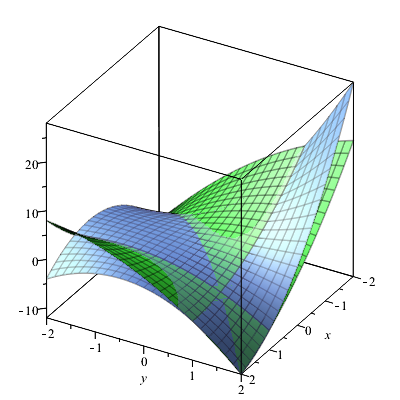
In de buurt van \((1,1)\) verschillen de functie en de Taylorbenadering niet veel; verder weg wel.
De lineaire en kwadratische benaderingen van functies van twee variabelen zijn afkomstig van de Stelling van Taylor van eerste en tweede orde.
Stelling van Taylor van eerste orde Bij een 'nette' functie \(f(x,y)\) van twee variabelen \(x\) en \(y\) geldt rondom het punt \((x,y)=(a,b)\) met \({\vartriangle}x=x-a\) en \({\vartriangle}y=y-b\): \[f(x,y) = f(a,b)+f_x(a,b){\vartriangle}x+f_y(a,b){\vartriangle}y+R_1(x,y)\] met restterm \(R_1(x,y)\) gegeven door \[R_1(x,y)=\frac{1}{2!}\left(f_{xx}(\xi,\eta){\vartriangle}x^2+2f_{xy}(\xi,\eta){\vartriangle}x{\vartriangle}y+f_{yy}(\xi,\eta){\vartriangle}y^2\right)\] voor zekere \(\xi\) tussen \(a\) en \(x\), en zekere \(\eta\) tussen \(b\) en \(y\).
Stelling van Taylor van tweede orde Bij een 'nette' functie \(f(x,y)\) van twee variabelen \(x\) en \(y\) geldt rondom het punt \((x,y)=(a,b)\) met \({\vartriangle}x=x-a\) en \({\vartriangle}y=y-b\): \[\begin{aligned}f(x,y) &= f(a,b)\\ &\phantom{=}+f_x(a,b){\vartriangle}x+f_y(a,b){\vartriangle}y\\ &\phantom{=}+ \frac{1}{2!}\left(f_{xx}(a,b){\vartriangle}x^2+2f_{xy}(a,b){\vartriangle}x{\vartriangle}y+f_{yy}(a,b){\vartriangle}y^2\right)+R_2(x,y)\end{aligned}\] met restterm \(R_2(x,y)\) gegeven door \[\begin{aligned}R_2(x,y) &= \frac{1}{3!}\Bigl(f_{xxx}(\xi,\eta){\vartriangle}x^3+3f_{xxy}(\xi,\eta){\vartriangle}x^2{\vartriangle}y\\ &\phantom{=xxx} +3f_{xyy}(\xi,\eta){\vartriangle}x{\vartriangle}y^2 +f_{yyy}(\xi,\eta){\vartriangle}y^3\Bigr)\end{aligned}\] voor zekere \(\xi\) tussen \(a\) en \(x\), en zekere \(\eta\) tussen \(b\) en \(y\).
Je kunt nog verder gaan, maar we laten het hierbij. De Taylorreeks bij functies van twee variabelen ziet er als volgt uit:
Taylorreeks Bij een 'nette' functie \(f(x,y)\) van twee variabelen \(x\) en \(y\) kunnen we functiewaarden rondom het punt \((x,y)=(a,b)\) benaderen via \[\begin{aligned}f(x,y) &= f(a,b)\\ &\phantom{=}+f_x(a,b){\vartriangle}x+f_y(a,b){\vartriangle}y\\ &\phantom{=}+ \frac{1}{2!}\left(f_{xx}(a,b){\vartriangle}x^2+2f_{xy}(a,b){\vartriangle}x{\vartriangle}y+f_{yy}(a,b){\vartriangle}y^2\right)\\ &\phantom{=}+ \frac{1}{3!}\Bigl(f_{xxx}(a,b){\vartriangle}x^3+3f_{xxy}(a,b){\vartriangle}x^2{\vartriangle}y\\ &\phantom{=xxxxx}+3f_{xyy}(a,b){\vartriangle}x{\vartriangle}y^2+f_{yyy}(a,b){\vartriangle}y^3\Bigl)\\ &\phantom{=}+\cdots\end{aligned}\] met \[{\vartriangle}x=x-a\quad\text{en}\quad {\vartriangle}y=y-b\tiny.\]


