Functions of several variables: Gradient
 The gradient
The gradient
The gradient of the function \(f(x,y)\) of two variables \(x\) and \(y\), denoted as \(\nabla f(x,y)\) and pronounced as 'nabla', is the vector of partial derivatives \[\nabla f(x,y)=\!\!\left(\begin{array}{c} f_x(x,y) \\ f_y(x,y)\end{array}\right)\]
\[f_x(x,y)=6 x\qquad\text{and}\qquad f_y(x,y)=-2\]
Thus, at the given point: \[f_x(-1,0)=-6\qquad\text{and}\qquad f_y(-1,0)=-2\] Thus, the gradient of \(f(x,y)\) at \((-1,0)\) is equal to the follwoing vector: \[\nabla f(-1,0)=\left(\begin{array}{c} -6\\ -2\end{array}\right)\]
The meaning of the gradient is clear when you realize that this is the vector such that the inner product with the direction vector \(\mathbf{dx} = \!\!\left(\begin{array}{c} \dd x \\ \dd y \end{array}\right)\) in the tangent plane of \(f\) at the point \(\bigl(x_0,y_0,f(x_0,y_0)\bigr)\) is equal to the total differential at \((x_0,y_0)\). So: \[\dd f(x_0,y_0)=\nabla f(x_0,y_0)\,\mathbf{\cdot}\, \mathbf{dx}\] Now suppose that the direction vector \(\mathbf{dx}\) has a constant length. then the total differential reaches its maxumum value when the direction vector has the same direction as the gradient. Similarly, the total differential reaches its minimum value when the direction is opposite to the gradient. The total differential is equal to \(0\) if and only if the gradient is perpendicular to the direction vector that corresponds with a projection of a level curve through the point \(\bigl(x_0,y_0,f(x_0,y_0)\bigr)\) on the \(xy\)-plane. So:
Geometric properties of the gradient The gradient at a point in the \(xy\)-plane indicates the (projected) direction in which the function \(f\) at the point \(\bigl(x,y,f(x,y)\bigr)\) increases most rapidly.
The gradient is perpendicular to the contour curve of \(f(x,y)\) at that point. The gradient is a normal vector of the tangent line at that point on the contour line.
The figure below illustrates the latter statement
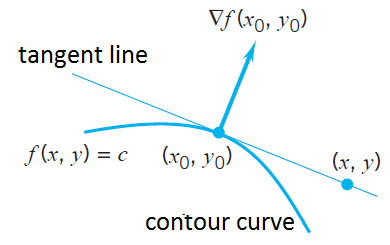
The equation of the tangent line is \[\nabla f(x_0,y_0)\,\mathbf{\cdot}\,\left(\begin{array}{c} x-x_0 \\ y-y_0\end{array}\right)=0\] So \[f_x(x_0,y_0)\cdot (x-x_0)+f_y(x_0,y_0) (y-y_0)=0\]
We find an equation of the tangent line at the point \((2,1)\) of the ellipse \[\frac{x^2}{4}+y^2=2\]. Note that the ellipse is a contour curve of the function \[f(x,y)=\frac{x^2}{4}+y^2\tiny.\] The partial derivatives of \(f(x,y)\) are \[f_x(x,y)=\frac{x}{2}\quad\text{and}\quad f_y(x,y)=2y\] The gradient of \(f\) at \((2,1)\) is \[\nabla f(2,1)=\!\!\left(\begin{array}{c} f_x(2,1) \\ f_y(2,1)\end{array}\right)=\!\!\left(\begin{array}{c} 1 \\ 2\end{array}\right)\] The tangent line at \((2,1)\) of the ellipse consists of points \((x,y)\) such that \[\nabla f(2,1)\,\mathbf{\cdot}\,\left(\begin{array}{c} x-2 \\ y-1\end{array}\right)=0\] Thus: \[1\cdot (x-2)+2\cdot (y-1)=0\] Expansion of the brackets gives \[x+2y-4=0\]
Higher dimensions One can similarly introduce the gradient for functions of three or more variables as a vector of partial derivatives. For example, for a function \(f(x,y,z)\) of three variables it is the vector \[\nabla f(x,y,z)=\!\!\left(\begin{array}{c} f_x(x,y,z) \\ f_y(x,y,z)\\ f_z(x,y,z)\end{array}\right)\]


