Functies van meer variabelen: Richtingsafgeleide en gradiënt
 Gradiënt
Gradiënt
De gradiënt van de functie \(f(x,y)\) van twee variabelen \(x\) en \(y\), genoteerd als \(\nabla f(x,y)\) en uit te spreken als 'nabla', is de vector van partiële afgeleiden \[\nabla f(x,y)=\!\!\left(\begin{array}{c} f_x(x,y) \\ f_y(x,y)\end{array}\right)\]
\[f_x(x,y)=2 x y-5 y-10 x\qquad\text{en}\qquad f_y(x,y)=x^2-5 x\]
Dus in het gegeven punt: \[f_x(0,1)=-5\qquad\text{en}\qquad f_y(0,1)=0\] Dus is de gradiënt van \(f(x,y)\) in \((0,1)\) gelijk aan de volgende vector \[\nabla f(0,1)=\left(\begin{array}{c} -5\\ 0\end{array}\right)\]
De betekenis van de gradiënt wordt duidelijk wanneer je je realiseert dat dit de vector is zodanig dat het inproduct met de richtingsvector \(\mathbf{dx}=\!\!\left(\begin{array}{c} \dd x \\\dd y\end{array}\right)\) in het raakvlak van \(f\) in het punt \(\bigl(x_0,y_0,f(x_0,y_0)\bigr)\) gelijk is aan de totale differentiaal in \((x_0,y_0)\). Dus: \[\dd f(x_0,y_0)=\nabla f(x_0,y_0)\,\mathbf{\cdot}\, \mathbf{\dd x}\] Veronderstel nu dat de richtingsvector \(\mathbf{dx}\) een constante lengte heeft. dan is de totale differentiaal maximaal wanneer de richtingsvector dezelfde richting heeft als de gradiënt. Evenzo is de totale differentiaal minimaal in de richting tegengesteld aan de gradiënt. De totale differentiaal is gelijk aan \(0\) dan en slechts dan als de gradiënt loodrecht op de richtingsvector staat, die hoort bij een projectie van een niveaukromme door het punt \(\bigl(x_0,y_0,f(x_0,y_0)\bigr)\) op het \(xy\)-vlak. Dus:
Meetkundige eigenschappen van de gradiënt De gradiënt in een punt in het \(xy\)-vlak geeft de (geprojecteerde) richting aan waarin de functie \(f\) in het punt \(\bigl(x,y,f(x,y)\bigr)\) het sterkst toeneemt.
De gradiënt staat loodrecht op de contourkromme van \(f(x,y)\) door dat punt. De gradiënt is een normaalvector van de raaklijn in dat punt aan die contourkromme.
Onderstaande figuur illustreert de laatste bewering
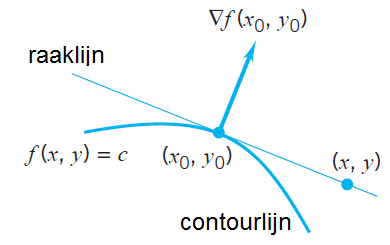
De vergelijking van de raaklijn is \[\nabla f(x_0,y_0)\,\mathbf{\cdot}\,\left(\begin{array}{c} x-x_0 \\ y-y_0\end{array}\right)=0\] Dus: \[f_x(x_0,y_0)\cdot (x-x_0)+f_y(x_0,y_0) (y-y_0)=0\]
We berekenen een vergelijking van de raaklijn aan de ellips \[\frac{x^2}{4}+y^2=2\] in het punt \((2,1)\). Merk op dat de ellips een contourkromme is van de functie \[f(x,y)=\frac{x^2}{4}+y^2\] De partiële afgeleiden van \(f(x,y)\) zijn \[f_x(x,y)=\frac{x}{2}\quad\text{en}\quad f_y(x,y)=2y\] De gradiënt van \(f\) in \((2,1)\) is \[\nabla f(2,1)=\!\!\left(\begin{array}{c} f_x(2,1) \\ f_y(2,1)\end{array}\right)=\!\!\left(\begin{array}{c} 1 \\ 2\end{array}\right)\] De raaklijn aan de ellips in \((2,1)\) bestaat uit punten \((x,y)\) zodanig dat \[\nabla f(2,1)\,\mathbf{\cdot}\,\left(\begin{array}{c} x-2 \\ y-1\end{array}\right)=0\] Dus: \[1\cdot (x-2)+2\cdot (y-1)=0\] oftewel \[x+2y-4=0\]
Hogere dimensies Ook bij functies van drie of meer variabelen kun je de gradiënt op analoge wijze introduceren als vector van partiële afgeleiden. Bijvoorbeeld voor functies \(f(x,y,z)\) van drie variabelen is het de vector \[\nabla f(x,y,z)=\!\!\left(\begin{array}{c} f_x(x,y,z) \\ f_y(x,y,z)\\ f_z(x,y,z)\end{array}\right)\]


