Functions of several variables: Critical points
 Introduction
Introduction
Review of critical points of functions of one variable We already know the concepts of critical point, maximum and minimum for functions of one variable. The function \(f(x)\) has a local minimum in \(x=a\) when the graph near \(x=a\) is above \(f(a)\), more precisely, if there is an interval \(I\) around \(a\) such that \(f(x)\ge f(a)\) for all \(x\) in \(I\).
A minimum (or maximum) of a differentiable function \(f(x)\) is always a critical point, that is, a point \(x=a\) at which the tangent line of \(f\) is horizontal, in other words \(f'(a)=0\). A sufficient condition for a minimum of \(f(x)\) at \(x=a\) is the second derivative criterion: if \(f'(a)=0\) and \(f''(a)>0\), then \(f(x)\) has a local minimum in \(x=a\).
With a second order Taylor approximation of the function \(f\) at \(x=a\) we can understand this as follows: if \(x=a\) is a critical point, then the Taylor polynomial of degree 2 at \(x=a\) is equal to \[f(a)+\tfrac{1}{2}f''(a)(x-a)^2\tiny.\] So the function is near \(x=a\) almost the same as a valley parabola with minimum \(x=a\) in case \(f''(a)>0\). If \(f''(a)<0\), then we are dealing with a mountain parabola with a maximum at \(x=a\).
If \(f'(a)=0\) and \(f''(a)=0\) you cannot conclude what kind of critical point \(x=a\) is: it might be a maximum or minimum, but it could also be an inflection point, i.e., a point where the derivative has a maximum or minimum. The figure below illustrates the three special points of a function of one variable.
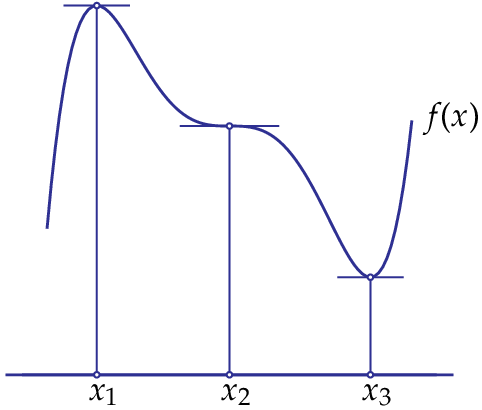
For functions of two or more variables we can set up a similar analysis, but even for functions of two variables this is already more complicated than you might expect.
For a differentiable function \(f\) of two or more variables, a point is called a critical point of \(f\) if the gradient of \(f\) at that point is the zero vector, in other words, if all first partial derivatives are zero at that point.
Geometrical property of a stationary For a function \(f(x,y)\) of two variables and a critical point \((a,b)\), the tangent plane of the graph of \(f\) at the stationary point \(\bigl(a,b,f(a,b)\bigr)\) is horizontal. After all, the normal vector of a tangent plane at the point \(\bigl(a,b,f(a,b)\bigr)\) is vertically oriented, because of the general formula for the normal vector of the tangent plane is given by \[\mathbf{n}=\left(\begin{array}{c} -f_x(a,b) \\ -f_y(a,b)\\ 1\end{array}\right)\] The linearization of the function (i.e., the first order Taylor approximation ) is at a critical point \((a,b)\) the constant function \(f(a,b)\).
Henceforth we will mainly focus in the analysis of functions of several variables on functions of two variables only.


