Functies van meer variabelen: Stationaire punten
 Inleiding
Inleiding
Repetitie van bijzondere punten van functies van één veranderlijke De begrippen stationair punt, maximum en minimum kennen we al voor functies van één variabele. De functie \(f(x)\) heeft een lokaal minimum in \(x=a\) als de grafiek in de buurt van \(x=a\) boven \(f(a)\) ligt, preciezer gezegd, als er een interval \(I\) om \(a\) is zodanig dat \(f(x)\ge f(a)\) voor alle \(x\) uit \(I\).
Bij een differentieerbare functie \(f(x)\) is een minimum (of maximum) steeds een stationair punt, dat wil zeggen een punt \(x=a\) waarin de raaklijn van \(f\) horizontaal is, oftewel \(f'(a)=0\). Een voldoende voorwaarde voor een minimum van \(f(x)\) in \(x=a\) is het tweede afgeleide criterium: Als \(f'(a)=0\) en \(f''(a)>0\), dan heeft \(f(x)\) een lokaal minimum in \(x=a\).
Met een Taylorbenadering van tweede orde rondom \(x=a\) kunnen we dit als volgt begrijpen: als \(x=a\) een stationair punt is, dan is de Taylorveelterm van graad 2 rondom \(x=a\) gelijk aan \[f(a)+\tfrac{1}{2}f''(a)(x-a)^2\tiny.\] In de buurt van \(x=a\) ziet de functie er dus uit als een dalparabool met minimum \(x=a\) als \(f''(a)>0\). In het geval \(f''(a)<0\), dan hebben we te maken met een bergparabool met maximum in \(x=a\).
Als \(f'(a)=0\) en \(f''(a)=0\) dan kun je nog niet concluderen wat voor een stationair punt \(x=a\) is: het kan een maximum of minimum zijn, maar het kan ook nog een buigpunt zijn, d.w.z. een punt waarin de afgeleide functie een maximum of minimum aanneemt. Onderstaande figuur illustreert de drie verschillende stationaire punten van een functie van één variabele.
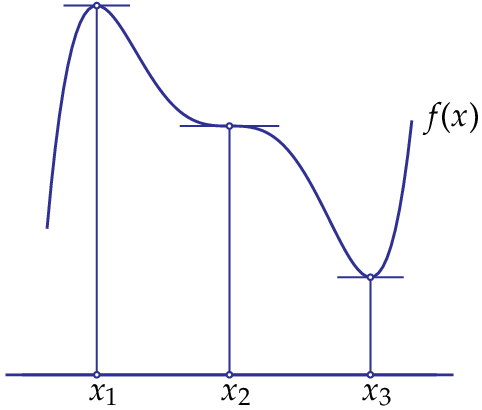
Voor functies van twee of meer variabelen kunnen we een soortgelijke analyse opzetten, maar deze is zelfs voor functies van twee variabelen al gecompliceerder dan je misschien denkt.
Bij een differentieerbare functie \(f\) van twee of meer variabelen heet een punt een stationair punt van \(f\) als de gradiënt van \(f\) daar de nulvector is, met andere woorden, als alle eerste partiële afgeleiden nul zijn in dat punt.
Meetkunde eigenschap van een stationair punt Bij een functie \(f(x,y)\) van twee variabelen is voor een stationair punt \((a,b)\) het raakvlak aan de grafiek in \(\bigl(a,b,f(a,b)\bigr)\) horizontaal. Immers, de normaalvector van een raakvlak in het punt \(\bigl(a,b,f(a,b)\bigr)\) is dan verticaal omdat de algemene formule voor de normaalvector van dit raakvlak gegeven is door \[\mathbf{n}=\left(\begin{array}{c} -f_x(a,b) \\ -f_y(a,b)\\ 1\end{array}\right)\] Voor een stationair punt \((a,b)\) is de linearisatie van de functie (oftewel de Taylorbenadering van eerste orde) de constante functie \(f(a,b)\).
In het vervolg zullen we ons in de analyse van functies van meer variabelen hoofdzakelijk beperken tot functies van twee variabelen.


