Functions of several variables: Critical points
 Maximum, minimum, and saddle point
Maximum, minimum, and saddle point
Below is the surface graph of the function \[f(x,y)=\tfrac{1}{2}\bigl(1-(x-\tfrac{1}{2})^2-(y-\tfrac{1}{2})^2\bigr)\]
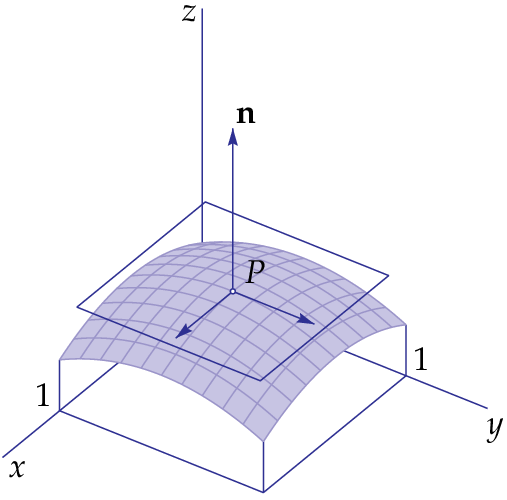
This function has first partial derivatives: \[f_x(x,y)=\tfrac{1}{2}-x\qquad\text{and}\qquad f_y(x,y)=\tfrac{1}{2}-y\] Both derivatives are zero at the point \((\tfrac{1}{2},\tfrac{1}{2})\) and thus is the tangent plane at the point \((\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2})\) horizontal. The point \((\tfrac{1}{2},\tfrac{1}{2})\) is a critical point and the function has a maximum value in that point.
Similar to the case of functions of one variable, it also holds for differentiable functions of two variables that being a critical point is a necessary but not sufficient condition for a point to be a maximum or minimum. We give a counterexample.
Below is the surface graph of the function \[f(x,y)=\tfrac{1}{2}\bigl(1-(x-\tfrac{1}{2})^2+(y-\tfrac{1}{2})^2\bigr)\]
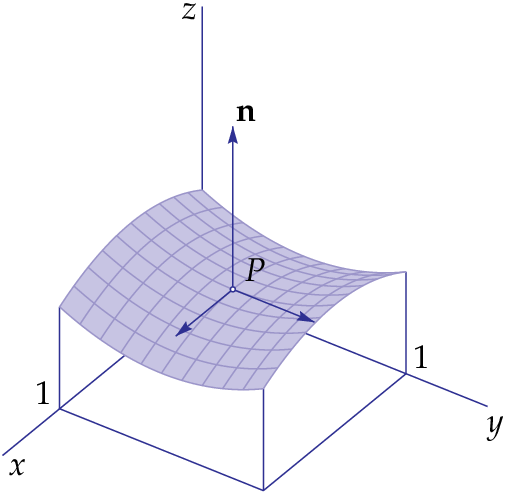
This function has first partial derivatives: \[f_x(x,y)=\tfrac{1}{2}-x\qquad\text{and}\qquad f_y(x,y)=y-\tfrac{1}{2}\] Both derivatives are zero at the point \((\tfrac{1}{2},\tfrac{1}{2})\) and thus is the tangent plane at the point \((\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2})\) horizontal. But the level curve through this point in the \(x\) direction is a mountain parabola, and the the level curve in the \(y\)direction is a valley parabola. Such a point is called a saddle point.
More generally, we say that the differentiable function \(f(x,y)\) has a saddle point \((a,b)\) if it is a critical point, but always points \((x,y)\) can be found near that point such that \(f(x,y)>f(a,b)\) as well as points such that \(f(x,y)<f(a,b)\). Loosely put, a saddle point is the two-dimensional analogue of an inflection point of a function of one variable.
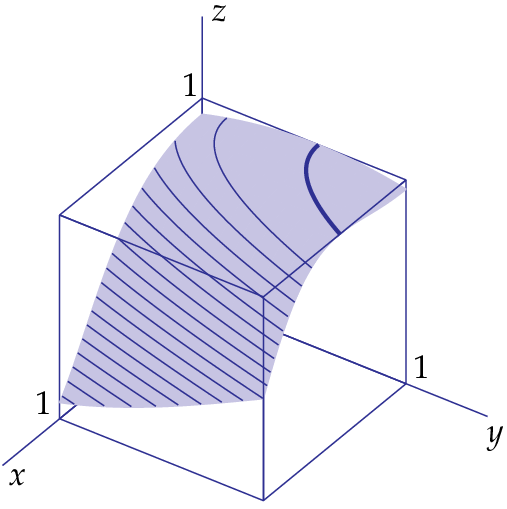
Up to now, critical points were always one or more disjoint points. But this need not always be the case. Consider, for example, the function \[f(x,y)=\tfrac{1}{2}\bigl(1-\sin(2x^2-y-1)\bigr)\] This function has first partial derivatives: \[f_x(x,y)=-2x\cos(2x^2-y-1)\qquad\text{andn}\qquad f_y(x,y)=\tfrac{1}{2}\cos(2x^2-y-1)\] The gradient is the zero vector in all points \((x,y)\) for which the following is true: \[\cos(2x^2-y-1)=0\] The critical points in this case are not isolated points, but points on curves, namely the parabolas \[2x^2-y-1=\tfrac{1}{2}\pi +k\pi\qquad\text{with integer }k\] One of these parabolas is \[y=2x^2-1-\tfrac{1}{2}\pi \] is drawn as a thick line in the graph below; it corresponds with the level curve of height \(1\). In all points of this parabola, the function reaches a maximum value. The corresponding tangent plane is the plane \(z=1\), the top face of the cube which is drawn around it.