Functies van meer variabelen: Stationaire punten
 Maximum, minimum en zadelpunt
Maximum, minimum en zadelpunt
Hieronder zie je de grafiek van de functie \[f(x,y)=\tfrac{1}{2}\bigl(1-(x-\tfrac{1}{2})^2-(y-\tfrac{1}{2})^2\bigr)\]
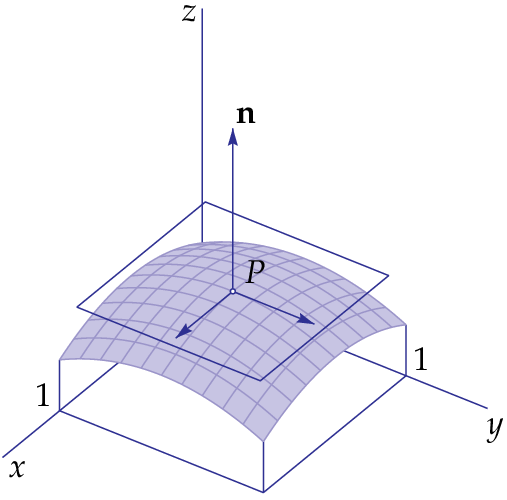
Deze functie heeft als partiële afgeleiden: \[f_x(x,y)=\tfrac{1}{2}-x\qquad\text{en}\qquad f_y(x,y)=\tfrac{1}{2}-y\] In het punt \((\tfrac{1}{2},\tfrac{1}{2})\) zijn beide afgeleiden nul en dus is het raakvlak in het punt \((\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2})\) horizontaal. Dit punt is een stationair punt en de functie heeft daar een maximale waarde.
Maar net als bij functies van één veranderlijke is voor differentieerbare functies van twee variabelen de eis dat een punt een stationair punt is noodzakelijk maar niet voldoende om een punt tot maximum of minimum uit te roepen. We geven een tegenvoorbeeld.
Hieronder zie je de grafiek van de functie \[f(x,y)=\tfrac{1}{2}\bigl(1-(x-\tfrac{1}{2})^2+(y-\tfrac{1}{2})^2\bigr)\]
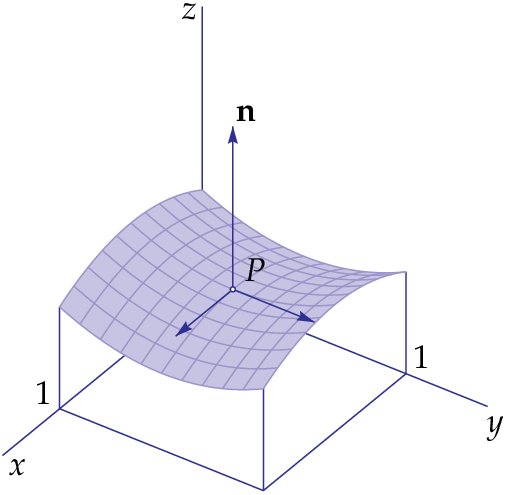
Deze functie heeft als partiële afgeleiden: \[f_x(x,y)=\tfrac{1}{2}-x\qquad\text{en}\qquad f_y(x,y)=y-\tfrac{1}{2}\] In het punt \((\tfrac{1}{2},\tfrac{1}{2})\) zijn beide afgeleiden weer nul en en dus is het raakvlak in het punt \((\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2})\) horizontaal. Maar de coördinatenlijn is in de richting van de \(x\)-as een bergparabool, en de coördinatenlijn is in de richting van de \(y\)-as een dalparabool. Zo'n punt wordt een zadelpunt genoemd.
Meer algemeen zeggen we dat de differentieerbare functie \(f(x,y)\) een zadelpunt \((a,b)\) heeft als het punt een stationair punt is, maar in de omgeving van het punt altijd punten \((x,y)\) te vinden zijn zodanig dat \(f(x,y)>f(a,b)\) én punten te vinden zijn zodanig dat \(f(x,y)<f(a,b)\). Losjes gezegd is een zadelpunt het tweedimensionale analogon van een buigpunt bij een functie van één variabele.
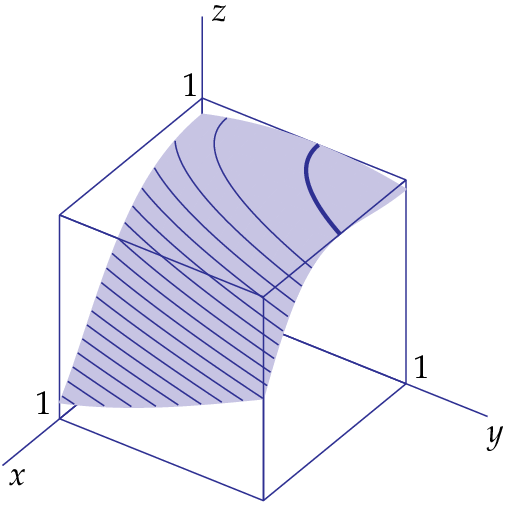
Tot nu toe waren stationaire punten steeds één of meer losse punten. Maar dit hoeft niet zo te zijn. Als voorbeeld nemen we de functie \[f(x,y)=\tfrac{1}{2}\bigl(1-\sin(2x^2-y-1)\bigr)\] Deze functie heeft als partiële afgeleiden: \[f_x(x,y)=-2x\cos(2x^2-y-1)\qquad\text{en}\qquad f_y(x,y)=\tfrac{1}{2}\cos(2x^2-y-1)\] De gradiënt is de nulvector in alle punten \((x,y)\) waarvoor geldt \[\cos(2x^2-y-1)=0\] De stationaire punten zijn in dit geval geen geïsoleerde punten, maar punten die krommen vormen, namelijk de parabolen \[2x^2-y-1=\tfrac{1}{2}\pi +k\pi\qquad\text{met geheel getal }k\] Een van deze parabolen is \[y=2x^2-1-\tfrac{1}{2}\pi \] die hoort bij de niveaukromme op hoogte \(1\) en deze kromme is in onderstaande grafiek dikker getekend. In alle punten van die parabool bereikt de functie een maximale waarde. Het bijbehorende raakvlak is het vlak \(z=1\), het bovenvlak van de kubus die eromheen is getekend.