Criteria voor extrema en zadelpunt

Functies van meer variabelen: Stationaire punten

Criteria voor extrema en zadelpunt

Onderstaande figuur illustreert het bestaan van lokale extrema en zadelpunten bij functies van twee variabelen.

bijzondere punten op een oppervlak

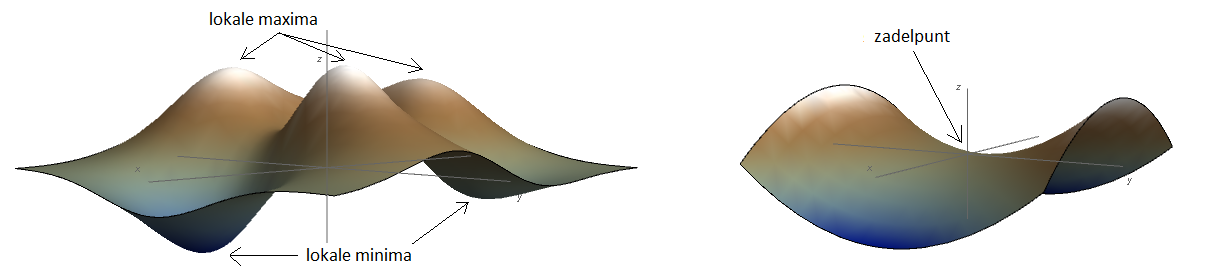
Net als bij functies van één variabelen willen we graag goed hanteerbare criteria hebben om het karakter van een stationair punt te kunnen bepalen. Hiervoor kijken we naar de Taylorbenadering van tweede orde van $f(x,y)$ rondom een stationair punt $(a,b)$ . Bij een 'nette' functie $f(x,y)$ van twee variabelen $x$ en $y$ hebben we al gezien dat we functiewaarden rondom het punt $(x,y)=(a,b)$ kunnen benaderen via $\begin{aligned}f(x,y) &\approx f(a,b)+f_x(a,b){\vartriangle}x+f_y(a,b){\vartriangle}y\\ &\phantom{=}+ \frac{1}{2}\!\!\left(f_{xx}(a,b){\vartriangle}x^2+2f_{xy}(a,b){\vartriangle}x{\vartriangle}y+f_{yy}(a,b){\vartriangle}y^2\right)\end{aligned}$ met ${\vartriangle}x=x-a\quad\text{en}\quad {\vartriangle}y=y-b\tiny.$ In het geval van een stationair punt vereenvoudigt dit tot $f(x,y) \approx f(a,b)+ \frac{1}{2}\!\!\left(f_{xx}(a,b){\vartriangle}x^2+2f_{xy}(a,b){\vartriangle}x{\vartriangle}y+f_{yy}(a,b){\vartriangle}y^2\right)$

Het gedrag van de tweede orde benadering van $f(x,y)$ rondom het stationaire punt $(a,b)$ wordt dus bepaalt door de kwadratische functie $h({\vartriangle}x, {\vartriangle}y)=f_{xx}(a,b){\vartriangle}x^2+2f_{xy}(a,b){\vartriangle}x{\vartriangle}y+f_{yy}(a,b){\vartriangle}y^2$

Als $h({\vartriangle}x,{\vartriangle}y)$ buiten $(0,0)$ alleen positieve waarden aanneemt, dan is $(a,b)$ een lokaal minimum van de functie $f(x,y)$ .
Als $h({\vartriangle}x,{\vartriangle}y)$ buiten $(0,0)$ alleen negatieve waarden aanneemt, dan is $(a,b)$ een lokaal maximum van de functie $f(x,y)$ .
Als $h({\vartriangle}x,{\vartriangle}y)$ buiten $(0,0)$ zowel positieve als negatieve waarden aanneemt, dan heeft de functie $f(x,y)$ een zadelpunt in $(a,b)$ .

Het verloop van $h(x,y)$ is nauw verbonden met de determinant van de Hesse matrix gedefinieerd als $\text{Hesse matrix van }f(x,y) = \left(\begin{array}{cc} f_{xx} & f_{xy} \\ f_{xy} & f_{yy}\end{array}\right)$ en uitgerekend in $(a,b)$ . De determinant van de Hesse matrix heet de disciminant of Hessiaan van $f(x,y)$ . We noteren $H(x,y)=f_{xx}(x,y)\cdot f_{yy}(x,y)-f_{xy}(x,y)^2$ en het verband met $h({\vartriangle}x,{\vartriangle}y)$ is (via kwadraatafsplitsen): $h({\vartriangle}x,{\vartriangle}y) = \frac{1}{f_{xx}(a,b)}\biggl((f_{xx}(a,b){\vartriangle}x+f_{xy}(a,b){\vartriangle}y)^2+{\vartriangle}y^2\cdot H(a,b)\biggr)$ We kunnen hieruit het volgende criterium destilleren:

Voor een 'nette' functie $f(x,y)$ en een stationair punt $(a,b)$ geldt:

Als $H(a,b)>0$ en $f_{xx}(a,b)>0$ , dan is $(a,b)$ een lokaal minimum van de functie $f(x,y)$ .
Als $H(a,b)>0$ en $f_{xx}(a,b)<0$ , dan is $(a,b)$ een lokaal maximum van de functie $f(x,y)$ .
Als $H(a,b)<0$ , dan heeft de functie $f(x,y)$ een zadelpunt $(a,b)$ .

waarbij $H(a,b)=\det\left(\begin{array}{cc} f_{xx}(a,b) & f_{xy}(a,b) \\ f_{xy}(a,b) & f_{yy}(a,b)\end{array}\right) = f_{xx}(a,b)\cdot f_{yy}(a,b)-f_{xy}(a,b)^2$

We bekijken opnieuw de functie $f(x,y)=3x^2y+xy^2-3xy$ De partiële afgeleiden zijn $f_x(x,y)=6xy+y^2-3y\qquad\text{en}\qquad f_y(x,y)=3x^2+2xy-3x$ De stationaire punten zijn dus de oplossingen van het stelsel vergelijkingen $\left\{\begin{aligned} 6xy+\phantom{2}y^2-3y&=0\\ 3x^2+2xy-3x&=0\end{aligned}\right.$ We hebben dit probleem al eerder opgelost: Er zijn dus vier stationaire punten: $(0,0)$ , $(1,0)$ , $(0,3)$ en $(\tfrac{1}{3},1)$ . We kijken nu naar de aard van deze stationaire punten.

We bereken eerst de partiële afgeleiden van tweede orde: $f_{xx}(x,y)=6y,\qquad f_{xy}(x,y)=6x+2y-3,\qquad f_{yy}(x,y)=2x.$ Met het volgende schema kunnen we uitspraken over de stationaire punten doen $\begin{array}{|c|c|c|c|c|c|} \hline (a,b) & f_{xx}(a,b) & f_{xy}(a,b) & f_{xy}(a,b) & H(a,b) & \textit{conclusie} \\ \hline (0,0) & 0 & -3 & 0 & -9 & \text{zadelpunt} \\ \hline (1,0) & 0 & 3 & 2 & -9 & \text{zadelpunt}\\ \hline (0,3) & 18 & 3 & 0 & -9 & \text{zadelpunt}\\ \hline (\tfrac{1}{3},1) & 6 & 1 & \tfrac{2}{3} & 3 & \text{minimum}\\ \hline \end{array}$

Contourkrommen in de nabijheid van de stationair punten zijn in onderstaande contourgrafiek getekend. Het patroon van gesloten krommen rondom een stationair punt (rondom $(\tfrac{1}{3},1)$ in dit voorbeeld) is typisch voor een lokaal maximum of minimum. Een kruising van krommen in een stationair punt (in $(0,-0), (1,0), (0,3)$ in dit voorbeeld) is kenmerkend voor een zadelpunt. Je ziet in deze punten ook vaak krommen die er langs afbuigen in een andere richting.

contourgrafiek en stationairepunten

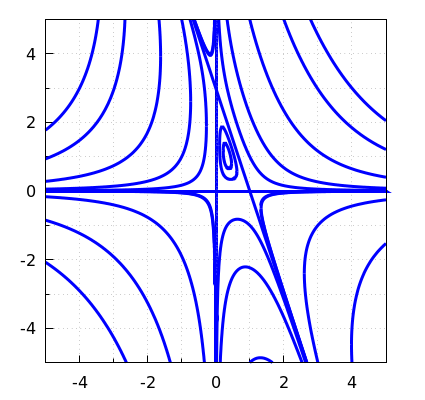
Onderstaande op de computer geconstrueerde grafiek van de functie met op een vlak geprojecteerde niveaukrommen illustreert de analyse (ook al zijn de niveaukrommen door numerieke afrondingsfouten minder netjes).

grafieken en stationairepunten

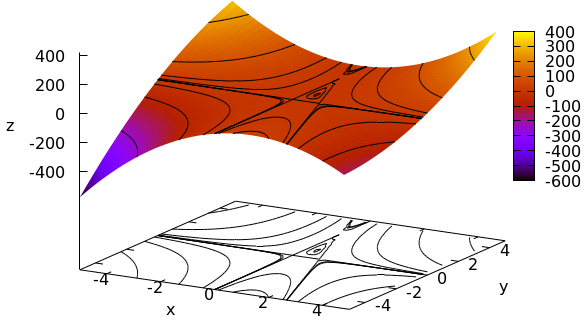
Bereken de extreme waarden van $f(x,y) = (x^2 + y) e^y$ Kandidaatpunten voor maxima en minima zijn de punten waar beide partiële afgeleiden nul zijn: $\frac{\partial f}{\partial x} (x,y) = 0 \quad\text{en}\quad \frac{\partial f}{\partial y} (x,y) 0$ Dit levert de volgende twee vergelijkingen op: $2x e^y = 0 \quad\text{en}\quad e^y + (x^2 + y) e^y = 0$ Omdat $e^y$ nooit nul is, volgt uit de eerste vergelijking dat $x = 0$ . Vullen we dit in de tweede vergelijking in, dan levert dit $e^y + y e^y = (1 + y) e^y = 0$ . Opnieuw omdat $e^y$ nooit nul is, zien we dat $y = -1$ .

Om te zien of het punt $(x,y) = (0,-1)$ een minimum, maximum, of zadelpunt is, berekenen we de tweede orde afgeleiden. We hebben
$\begin{aligned} \frac{\partial^2 f}{\partial x^2} (x,y) &= 2 e^y \\ \\ \frac{\partial^2 f}{\partial x\partial y} (x,y) &= 2x e^y \\ \\ \frac{\partial^2 f}{\partial y^2} (x,y) &= 2 e^y + (x^2 + y) e^y\end{aligned}$
Dus is de Hesse matrix in het gegeven punt gelijk aan $\left( \begin{array}{cc} \dfrac{\partial^2 f}{\partial x^2} (0,-1) & \dfrac{\partial^2 f}{\partial x\partial y} (0,-1) \\ \dfrac{\partial^2 f}{\partial x\partial y} (0,-1) & \dfrac{\partial^2 f}{\partial y^2} (0,-1) \end{array} \right) = \left( \begin{array}{cc} 2/e & 0 \\ 0 & 1/e \end{array} \right)$ Omdat de determinant van deze matrix positief is, en het element linksboven ook positief is, geeft het punt $(0,-1)$ een minimum.

Beschouw het vlak $V = \{ 2x - y + z = 1\}$ en het punt $(-4,1,3)$ in ${\mathbb R}^3$ . Wat is de kleinste afstand van dit punt tot het vlak?

De afstand van $(-4,1,3)$ tot een punt $(x,y,z)$ dat in $V$ ligt, is gelijk aan $\sqrt{(x+4)^2 + (y-1)^2 + (z-3)^2}\text.$ Deze afstand willen we minimaliseren. Nu is de wortel uit $(x+4)^2 + (y-1)^2 + (z-3)^2$ minimaal precies als $(x+4)^2 + (y-1)^2 + (z-3)^2$ minimaal is, en kunnen we deze kwadratische functie minimaliseren. Voor $(x,y,z)$ in $V$ geldt $z = 1-2x+y$ . Als we dit in de kwadratische functie invullen, krijgen we de volgende functie van twee variabelen $(x,y)$ die we moeten minimaliseren: $f(x,y) = (x+4)^2 + (y-1)^2 + (y-2x-2)^2$ Bereken $Df (x,y) = \left( \begin{array}{cc} 2 (x+4) - 4(y-2x -2) & 2(y-1) + 2(y-2x-2) \end{array}\right)$ Beide elementen van de matrix $Df(x,y)$ moeten nul zijn in een minimum. Dit levert de twee vergelijkingen op: $\Biggl\{ \begin{array}{c} 2 (x+4) - 4(y-2x -2) = 0 \\ 2(y-1) + 2(y-2x-2)=0 \end{array}$ oftewel $\Biggl\{ \begin{array}{c} 10 x -4 y + 16 = 0 \\ -4 x + 4y -6 =0\end{array}$ De oplossing hiervan is $(x,y) = (-\tfrac{5}{3},-\tfrac{1}{6})$ , waarvoor $f(-\tfrac{5}{3},-\tfrac{1}{6}) = (\tfrac{14}{6})^2 + (-\tfrac{7}{6})^2 + (\tfrac{7}{6})^2 = \tfrac{49}{6}$ De Hesse matrix van tweede orde partiële afgeleiden is $\left( \begin{array}{cc} 10 & -4 \\ -4 & 4 \end{array}\right)$ Hieraan zien we bevestigd dat het een minimum betreft (waarom ook al weer?). Ergo, de minimale afstand van $(-4,1,3)$ tot het vlak $V$ is $\sqrt{\tfrac{49}{6}}$ , en het punt op $V$ dat het dichtst bij $(-4,1,3)$ ligt, is $(-\tfrac{5}{3},-\tfrac{1}{6},\tfrac{25}{6})$ .