Matlab provides plenty of functionality to create graphs of functions of two variables. This can be done in various ways. It is possible to define a function that computes the values of $z$ for given $x$ and $y$values. It is also possible to work with a meshgrid, in the $x$ and $y$ direction, and determine the associated $z$ values (in the mesh points). Hereafter this can be plotted as a surface plot(surf) or a mesh plot (mesh). We will mainly use the latter method.

In other programming languages, it is quite common to work in an object-oriented style. In Matlab this is less important which of the graphing styles you select. Even in the creation of different axes in one axis direction or in the construction of several graphs in one figure it is not necessary to work in an object-oriented style. Matlab namely applies an operation to the figure, or the coordinate system which is defined for graphing. Placement of the operations in the proper order is then sufficient.

Below we show various ways to plot functions (though there are other possibilities).

OO visualization versus the procedural approach

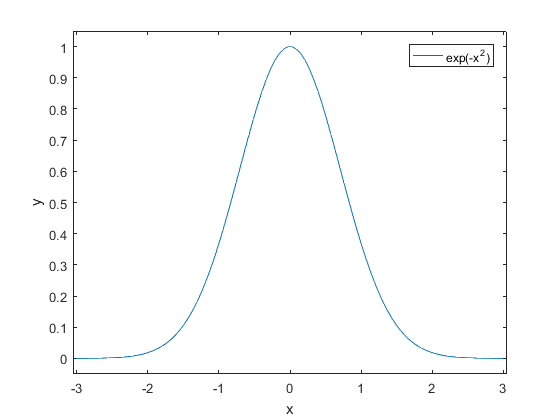
We start just in two dimensions and plot the graph of the function $f(x)=e^{-x^2}$.

In the non-object-oriented approach to plotting the graph of a function $f$ of one variable one can proceed as follows.

>> x = linspace(-3,3,100); 
>> y = exp(-x.^2); 
>> % Below is the plotting part of the code 
>> plot(x,y) >> legend('exp(-x^{2})') 
>> xlabel('x') >> ylabel('y') 
>> xlim([-3.05,3.05]) 
>> ylim([-0.05,1.05])

In the object-oriented style, the plotting part of the code after the function definition goes as follows: first you introduce a Figure instance, named fig, and herewith you construct an Axis instance, named ax. Hereafter, you adjust the properties of the instance ax. Of course other names of instances may be used

>> x = linspace(-3,3,100); 
>> y = exp(-x.^2); 
>> fig = figure('Color','White'); 
>> ax = fig.CurrentAxes; 
>> plot(x,y) 
>> ax.XLabel.String = 'x'; 
>> ax.YLabel.String = 'y'; 
>> lgd = legend(['exp(-t^2)']); 
>> ax.XLim = [-3.05, 3.05]; 
>> ax.YLim = [-0.05, 1.05];

In both cases the result is the following picture.

The example below shows for both methods how you can add a part of the graph above as an inset.

Using the first method:

>> x = linspace(-3,3,100); 
>> y = exp(-x.^2); 
>> fig = figure('Color','White'); 
>> ax1 = axes('Position',[0.1 0.1 0.85 0.85]); 
>> plot(x,y,'b-','Parent',ax1) 
>> xlabel(ax1,'x') 
>> ylabel(ax1,'y') 
>> lgd = legend(['exp(-t^2)']); 
>> xlim(ax1,[-3.05, 3.05]); 
>> ylim(ax1,[-0.05, 1.05]); 
>> ax2 = axes('Position',[0.16, 0.60, 0.22, 0.32]);  % Inset 
>> plot(x(33:68),y(33:68),'g-','Parent',ax2) % Part of diagram 
>> xlim(ax2,[x(33)-0.01, x(68)+0.01]); 
>> ylim(ax2,[0.35, 1.05]);

Via the more object-oriented method:

>> x = linspace(-3,3,100); 
>> y = exp(-x.^2); 
>> fig = figure('Color','White'); 
>> ax1 = axes('Position',[0.1 0.1 0.85 0.85]); 
>> plot(x,y,'b-','Parent',ax1) 
>> ax1.XLabel.String = 'x'; 
>> ax1.YLabel.String = 'y'; 
>> lgd = legend(['exp(-t^2)']); 
>> ax1.XLim = [-3.05, 3.05]; 
>> ax1.YLim = [-0.05, 1.05]; 
>> ax2 = axes('Position',[0.16, 0.60, 0.22, 0.32]);  % Inset 
>> plot(x(33:68),y(33:68),'g-','Parent',ax2)  % Part of diagram 
>> ax2.XLim = [x(33)-0.01, x(68)+0.01]; 
>> ax2.YLim = [0.35, 1.05];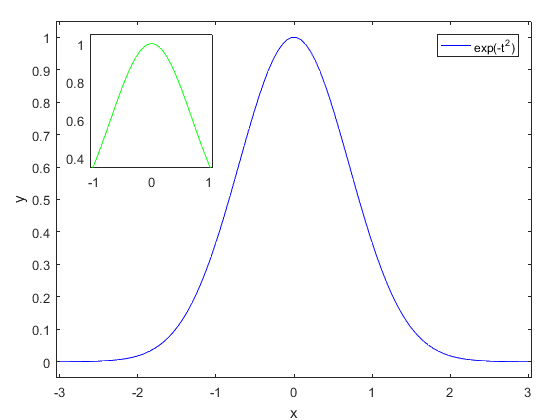

With the subplot command you can divide the canvas into several pieces.

Graph of a function of two variables

We draw the graph of the function $z=f(x,y)=e^{-x^2-y^2}$. For this purpose, it is necessary to define first the $x$ and $y$ values as a linspace. These homogeneously distributed vectors are then used to create a meshgrid. For each coordinate $(x,y)$ in the grid, the corresponding value of $z$ is determined by vector calculation with the desired function. We make a surface plot (surf) to plot the graph in 3D. The number of coordinates that occurs in the lattice is determined by the number of points in the linspace for $x$ and $y$ is imparted. The more coordinates, the smoother the surface is. Below we selected a $50 \times 50$ grid to plot the graph.

>> x = linspace(-4,4,50); 
 >> y = linspace(-4,4,50); 
 >> [x,y] = meshgrid(x,y); 
 >> z = exp(-x.^2-y.^2); 
 >> fig = figure('Color','White'); 
 >> surf(x,y,z) 
 >> xlabel('X') 
 >> ylabel('Y') 
 >> zlabel('Z') 
 >> xlim([-4,4]) 
 >> ylim([-4,4]) 
 >> zlim([0,1])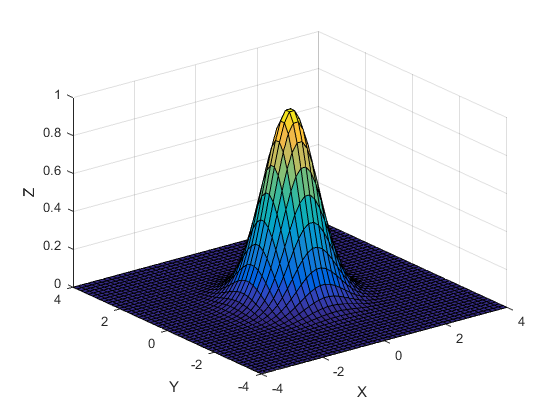

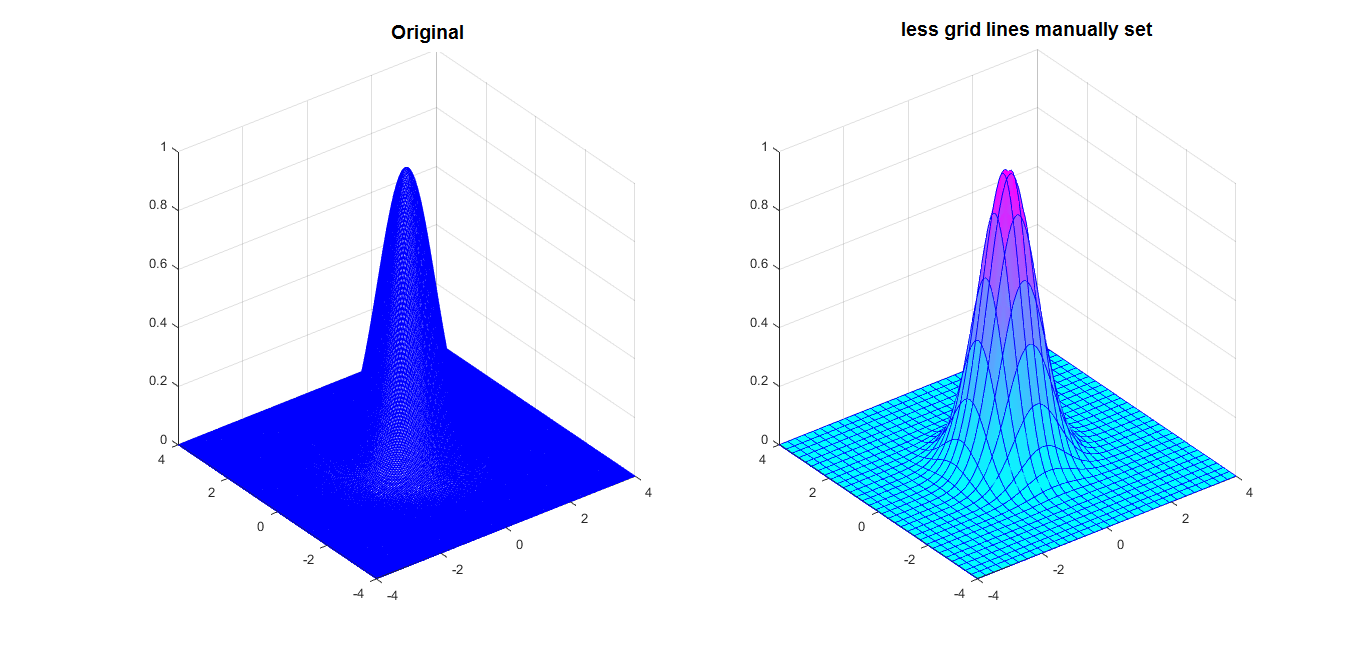
In Matlab all grid lines are plotted. If you need a very smooth figure for which many grid points must be specified, this may cause the resulting surface to look uniformly coloured (whatever colormap you have chosen). In this case it may be a good option to turn off the grid lines. When you only have a combination of a very smooth surface and not too many grid lines you can plot with default settings, and you can still adjust the plot manually afterwards.

>> x = linspace(-4,4,300); 
>> y = linspace(-4,4,300); 
>> [x,y] = meshgrid(x,y); 
>> z = exp(-x.^2-y.^2); 
>> fig = figure('Color','White'); 
>> ax1 = subplot(1,2,1); 
>> mesh(x,y,z,'EdgeColor','b') % Original plot 
>> colormap cool  % The colormap is not clear 
>> [az,el] = view;  % Get the azimuth and elevation angles for this plot
>> ax2 = subplot(1,2,2);
>> % Reduce the number of plotted grid lines 
>> rskip = round(linspace(1,size(z,1),32)); 
>> cskip = round(linspace(1,size(z,2),32)); 
>> hold on 
>> surf(x(rskip,:),y(rskip,:),z(rskip,:),'EdgeColor','b','MeshStyle','row'); 
>> surf(x(:,cskip),y(:,cskip),z(:,cskip),'EdgeColor','b','MeshStyle','column'); 
>> colormap cool  % Now the colormap is visible 
>> grid on 
>> view(az,el)  % Set the azimuth and elevation angles as for the plot to the left 
>> hold off

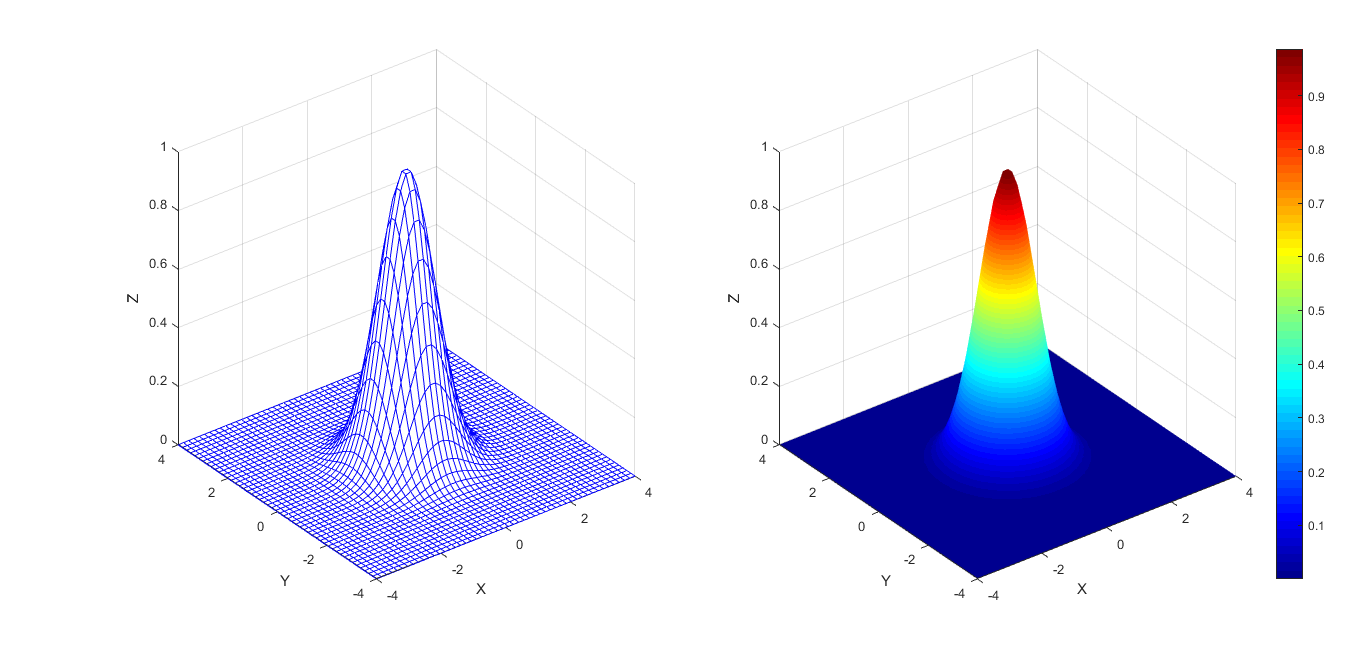
Below are two other visualizations: a wire frame presentation and a more beautiful and informative graph with colouring based on the $z$ value.

>> x = linspace(-4,4,50); 
>> y = linspace(-4,4,50); 
>> [x,y] = meshgrid(x,y); 
>> z = exp(-x.^2-y.^2); 
>> fig = figure('Color','White'); 
>> ax1 = subplot(1,2,1); 
>> mesh(x,y,z,'EdgeColor','Blue','Parent',ax1) 
>> xlabel('X') >> ylabel('Y') 
>> zlabel('Z') 
>> xlim([-4,4]) >> ylim([-4,4]) 
>> zlim([0,1]) >> ax2 = subplot(1,2,2); 
>> surf(x,y,z,'Parent',ax2); 
>> originalSize = get(ax2, 'Position'); 
>> colormap jet 
>> shading interp 
>> cbar = colorbar(ax2); 
>> cbar.Position = [0.95,0.1,0.01,0.7]; % Adding the colorbar resizes the subplot. Use 'originalSize' to resize to original dimensions. 
>> set(ax2, 'Position', originalSize); >> xlabel('X') >> ylabel('Y') >> zlabel('Z')