Matlab levert ook de functionaliteit om grafieken van functies van twee variabelen te creëren. Dit kan op verschillende manieren. Het is mogelijk om een functie te definiëren die de waarden van \(z\) bij gegeven \(x\) en \(y\) bepaald. Ook is het mogelijk om te werken met een meshgrid, in de \(x\) en \(y\) richting, en hier de bijbehorende \(z\) waarden bij de bepalen. Dit wordt dan vervolgens geplot met behulp van een surface (surf) of een meshplot (mesh). Wij zullen vooral deze laatste methode gebruiken.

Bij andere programmeertalen is het gebruikelijk om in een object-georiënteerde stijl te werken. In Matlab is het minder belangrijk welk van de stijlen je kiest. Ook bij het creëren van verschillende assen in één asrichting, of verscheidene grafieken in één figuur is het niet noodzakelijk om object-georiënteerd te werken. Matlab past een bepaalde bewerking namelijk toe op de figuur of het assenstelsel dat ervoor gedefinieerd is. Het in de juiste volgorde plaatsen van de bewerkingen is dan voldoende.

Hieronder laten we verschillende manieren zien (er zijn echter nog meer mogelijkheden).

OO visualisatie versus de procedurele aanpak

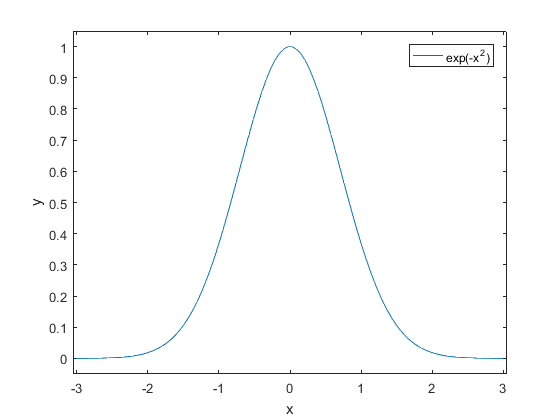
We beginnen in twee dimensies en tekenen de grafiek van de functie \(f(x)=e^{-x^2}\).

In de niet object-georiënteerde aanpak kan het tekenen van de grafiek van een functie \(f\) in één veranderlijke als volgt gaan.

>> x = linspace(-3,3,100);
>> y = exp(-x.^2);
>> % Hierna komt het plot gedeelte
>> plot(x,y)
>> legend('exp(-x^{2})')
>> xlabel('x')
>> ylabel('y')
>> xlim([-3.05,3.05])
>> ylim([-0.05,1.05])

In object-georiënteerde stijl gaat het plot-gedeelte na de functiedefinitie als volgt: eerst introduceer je een Figure instantie, fig genaamd, en daarmee creëer je een Axis instantie, ax genaamd. Daarna pas je de eigenschappen van de instantie ax aan. Natuurlijk mag je ook andere namen voor instanties gebruiken, maar wij hebben traditionele keuzes gemaakt.

>> x = linspace(-3,3,100);
>> y = exp(-x.^2);
>> fig = figure('Color','White');
>> ax = fig.CurrentAxes;
>> plot(x,y)
>> ax.XLabel.String = 'x';
>> ax.YLabel.String = 'y';
>> lgd = legend(['exp(-t^2)']);
>> ax.XLim = [-3.05, 3.05];
>> ax.YLim = [-0.05, 1.05];

In beide gevallen is het resultaat het volgende plaatje.

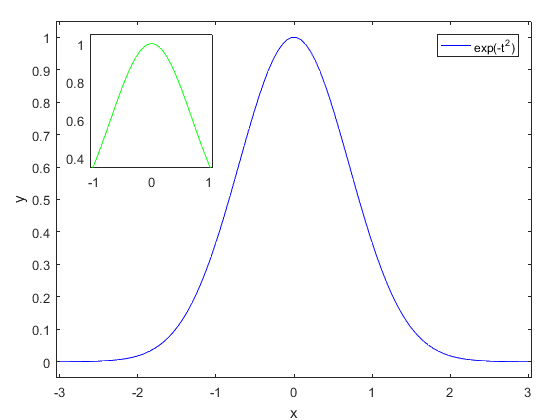
Onderstaand voorbeeld laat voor beide methodes zien hoe je een deel van de voorgaande grafiek kunt toevoegen als inzetsel.

Via de eerste methode:

>> x = linspace(-3,3,100);
>> y = exp(-x.^2);
>> fig = figure('Color','White');
>> ax1 = axes('Position',[0.1 0.1 0.85 0.85]); 
>> plot(x,y,'b-','Parent',ax1)
>> xlabel(ax1,'x')
>> ylabel(ax1,'y')
>> lgd = legend(['exp(-t^2)']);
>> xlim(ax1,[-3.05, 3.05]);
>> ylim(ax1,[-0.05, 1.05]);
>> ax2 = axes('Position',[0.16, 0.60, 0.22, 0.32]); % Inzetsel
>> plot(x(33:68),y(33:68),'g-','Parent',ax2) % Deeldiagram
>> xlim(ax2,[x(33)-0.01, x(68)+0.01]);
>> ylim(ax2,[0.35, 1.05]);

Via de meer object georiënteerde methode:

>> x = linspace(-3,3,100);
>> y = exp(-x.^2);
>> fig = figure('Color','White');
>> ax1 = axes('Position',[0.1 0.1 0.85 0.85]); 
>> plot(x,y,'b-','Parent',ax1)
>> ax1.XLabel.String = 'x';
>> ax1.YLabel.String = 'y';
>> lgd = legend(['exp(-t^2)']);
>> ax1.XLim = [-3.05, 3.05];
>> ax1.YLim = [-0.05, 1.05];
>> ax2 = axes('Position',[0.16, 0.60, 0.22, 0.32]); % Inzetsel
>> plot(x(33:68),y(33:68),'g-','Parent',ax2) % Deeldiagram
>> ax2.XLim = [x(33)-0.01, x(68)+0.01];
>> ax2.YLim = [0.35, 1.05];

Met het subplot commando kun je het tekengebied in verschillende stukken verdelen.

Grafiek van een functie van twee variabelen

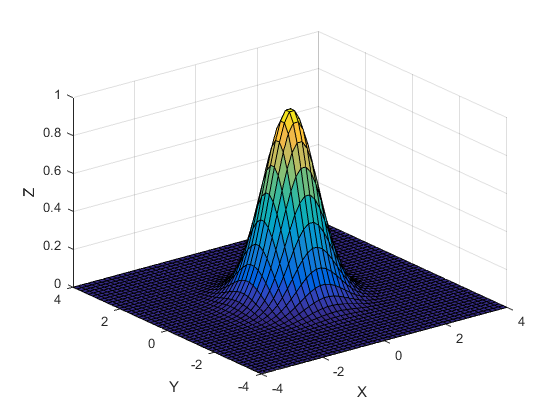
We tekenen nu de grafiek van de functie \(f(x,y)=e^{-x^2-y^2}\). Hiervoor is het nodig om de \(x\) en \(y\) waarden eerst te definiëren als een linspace. Deze homogeen verdeelde vectoren worden vervolgens gebruikt om een meshgrid te maken. Bij elk coördinaat \((x,y)\) in het rooster wordt de bijbehorende waarde voor \(z\) bepaald via vectorrekening in de gewenste functie. We gebruiken een surface (surf) om de grafiek in 3D te plotten. Het aantal coördinaten dat in het rooster voorkomt wordt bepaald door het aantal punten dat in de linspace voor \(x\) en \(y\) wordt meegegeven. Hoe meer coördinaten, des te gladder is het oppervlak. Hieronder is gekozen voor een \(50 \times 50\) rooster.

>> x = linspace(-4,4,50);
>> y = linspace(-4,4,50);
>> [x,y] = meshgrid(x,y);
>> z = exp(-x.^2-y.^2);
>> fig = figure('Color','White');
>> surf(x,y,z)
>> xlabel('X')
>> ylabel('Y')
>> zlabel('Z')
>> xlim([-4,4])
>> ylim([-4,4])
>> zlim([0,1])

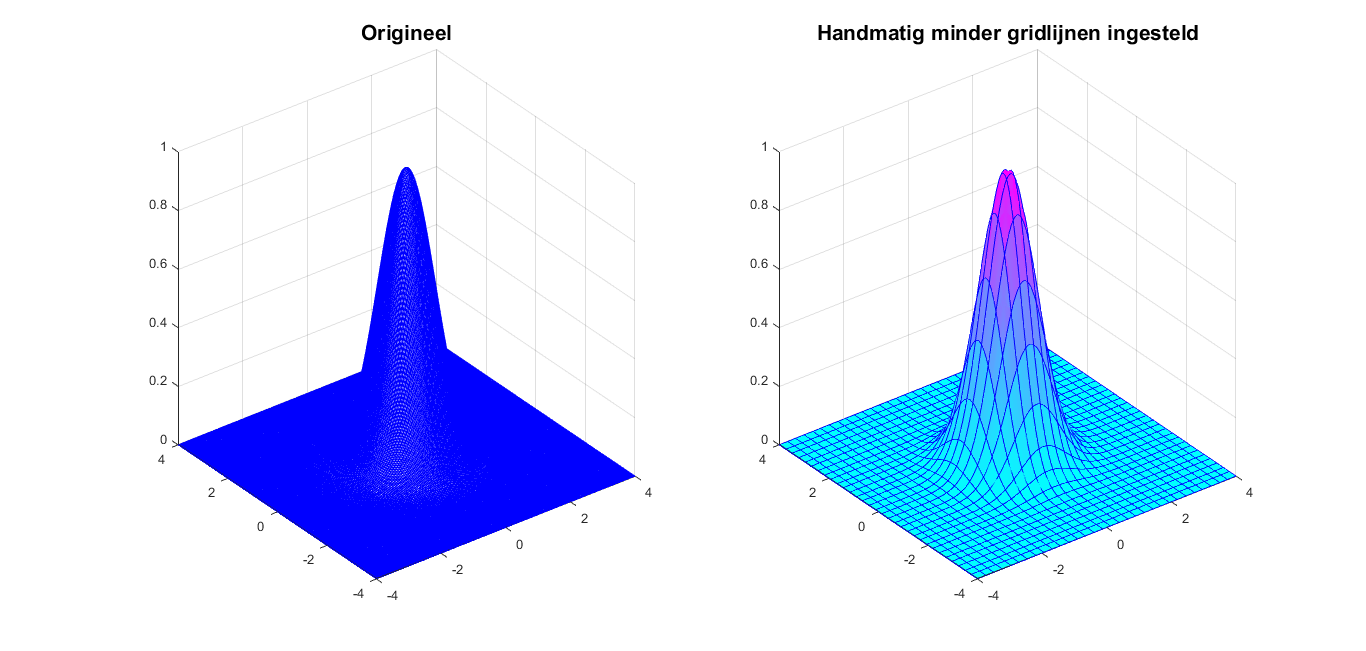
In Matlab worden alle roosterlijnen geplot. Als er een hele gladde figuur nodig is waarvoor heel veel roosterpunten gespecificeerd moeten worden, kan dit ertoe leiden dat het resulterende oppervlak er homogeen gekleurd uit ziet (ongeacht de colormap die je hebt gekozen). Dan kan het een goede optie zijn om de roosterlijnen uit te zetten. Mocht er echter een combinatie nodig zijn van een heel glad oppervlak en minder roosterlijnen dan er standaard geplot worden, dan is dit achteraf handmatig mogelijk.

>> x = linspace(-4,4,300);
>> y = linspace(-4,4,300);
>> [x,y] = meshgrid(x,y);
>> z = exp(-x.^2-y.^2);
>> fig = figure('Color','White');
>> ax1 = subplot(1,2,1);
>> mesh(x,y,z,'EdgeColor','b') % Originele plot
>> colormap cool % De colormap is niet te zien
>> [az,el] = view; % Sla de kijkhoeken op
>> ax2 = subplot(1,2,2);
>> rskip = round(linspace(1,size(z,1),32));
>> cskip = round(linspace(1,size(z,2),32));
>> hold on
>> surf(x(rskip,:),y(rskip,:),z(rskip,:),'EdgeColor','b','MeshStyle','row');
>> surf(x(:,cskip),y(:,cskip),z(:,cskip),'EdgeColor','b','MeshStyle','column');
>> colormap cool % Nu is de toegepaste colormap wel te zien
>> grid on
>> view(az,el) % Stel de kijkhoeken gelijk aan die voor de linker grafiek.
>> hold off

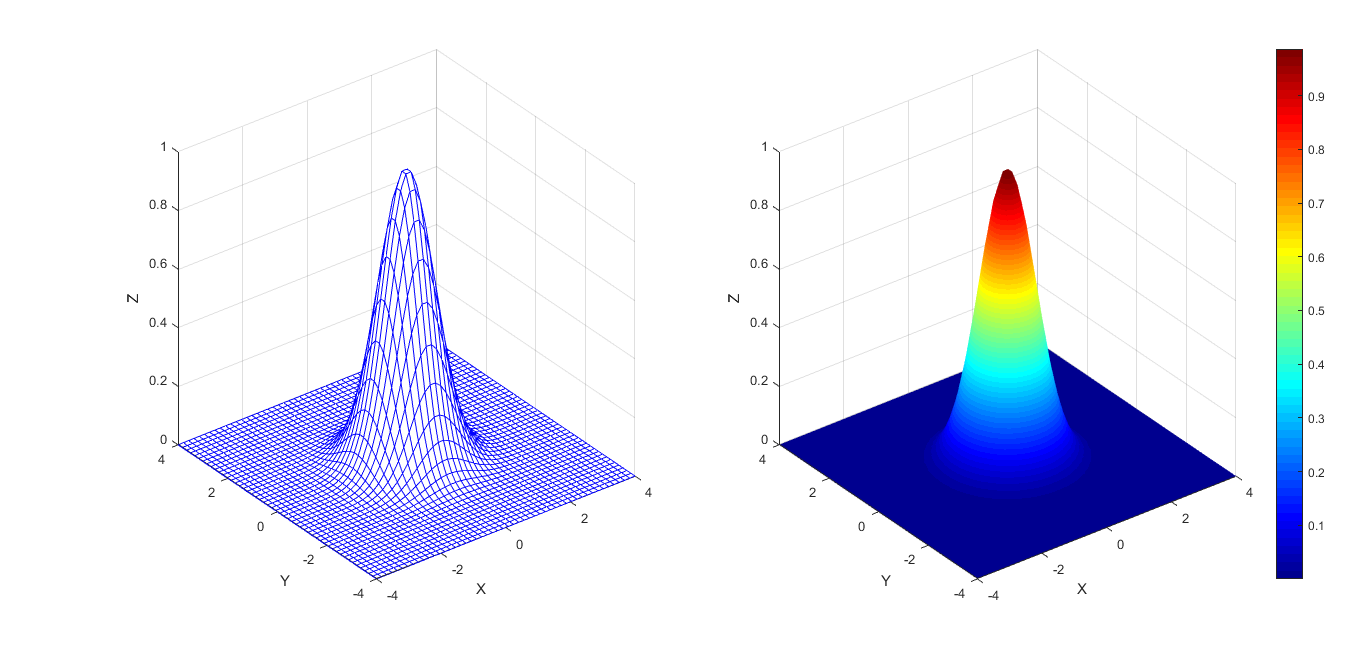
Hieronder staan twee andere visualisaties: een draadraam-presentatie en een veel fraaiere en meer informatieve grafiek met kleuring op basis van \(z\)-waarde.

>> x = linspace(-4,4,50);
>> y = linspace(-4,4,50);
>> [x,y] = meshgrid(x,y);
>> z = exp(-x.^2-y.^2);
>> fig = figure('Color','White');
>> ax1 = subplot(1,2,1);
>> mesh(x,y,z,'EdgeColor','Blue','Parent',ax1)
>> xlabel('X')
>> ylabel('Y') 
>> zlabel('Z') 
>> xlim([-4,4]) 
>> ylim([-4,4])
>> zlim([0,1])
>> ax2 = subplot(1,2,2);
>> surf(x,y,z,'Parent',ax2);
>> originalSize = get(ax2, 'Position'); 
>> colormap jet
>> shading interp
>> cbar = colorbar(ax2); 
>> cbar.Position = [0.95,0.1,0.01,0.7];
>> set(ax2, 'Position', originalSize);
>> % Met de kleurenbalk verandert de grootte van de subplot. Met 'originalSize' voorkom je dit
>> xlabel('X')
>> ylabel('Y')
>> zlabel('Z')