Opdracht 1

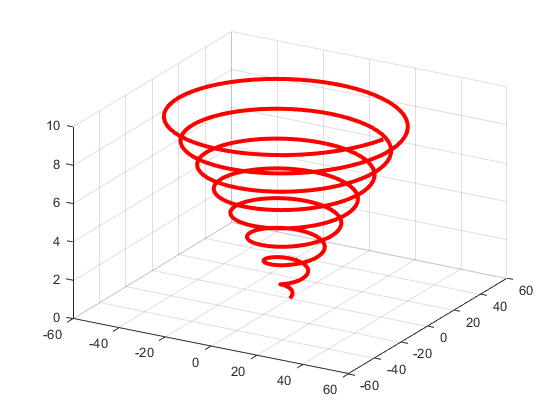
Om de grafiek van de functie \[f(x,y)=\tfrac{1}{2}\!\bigl(1-\sin(2x^2-y-1)\bigr)\] te plotten maken we eerst een meshgrid en gebruiken we daarna het commando surf om de informatie als een surface te plotten. Het commando contour resulteert in de contouren in 3D zonder een opppervlak. We combineren beide commando's voor het gewenste resultaat. Om ervoor te zorgen dat de contourlijnen zichtbaar zijn zetten we de 'FaceAlpha' eigenschap van het oppervlak op \(0.5\). Daarnaast gebruiken we subplot om zowel het 3D resultaat als een gewone 2D contourplot te laten zien.

>> x = linspace(-3,3,500);
>> y = linspace(-3,3,500);
>> [x,y] = meshgrid(x,y);
>> z = 0.5.*(1-sin(2.*x.^2-y-1));
>> fig = figure('Color','White');
>> ax1 = subplot(1,2,1);
>> surf(x,y,z,'EdgeColor','none','FaceAlpha',0.5)
>> colormap(jet)
>> hold on
>> contour3(x,y,z)
>> xlabel('X')
>> ylabel('Y')
>> zlabel('Z')
>> xlim([-1.5,1.5])
>> ylim([-1.5,1.5])
>> zlim([0,1])
>> view(120,35)
>> ylim([-1.5,1.5])
>> ax2 = subplot(1,2,2);
>> contour(x,y,z,'Parent',ax2);
>> colormap(jet)
>> xlabel('x')
>> ylabel('y')
>> xlim([-1.5,1.5])
>> ylim([-1.5,1.5])
>> axis square

Dit geeft het volgende resultaat:

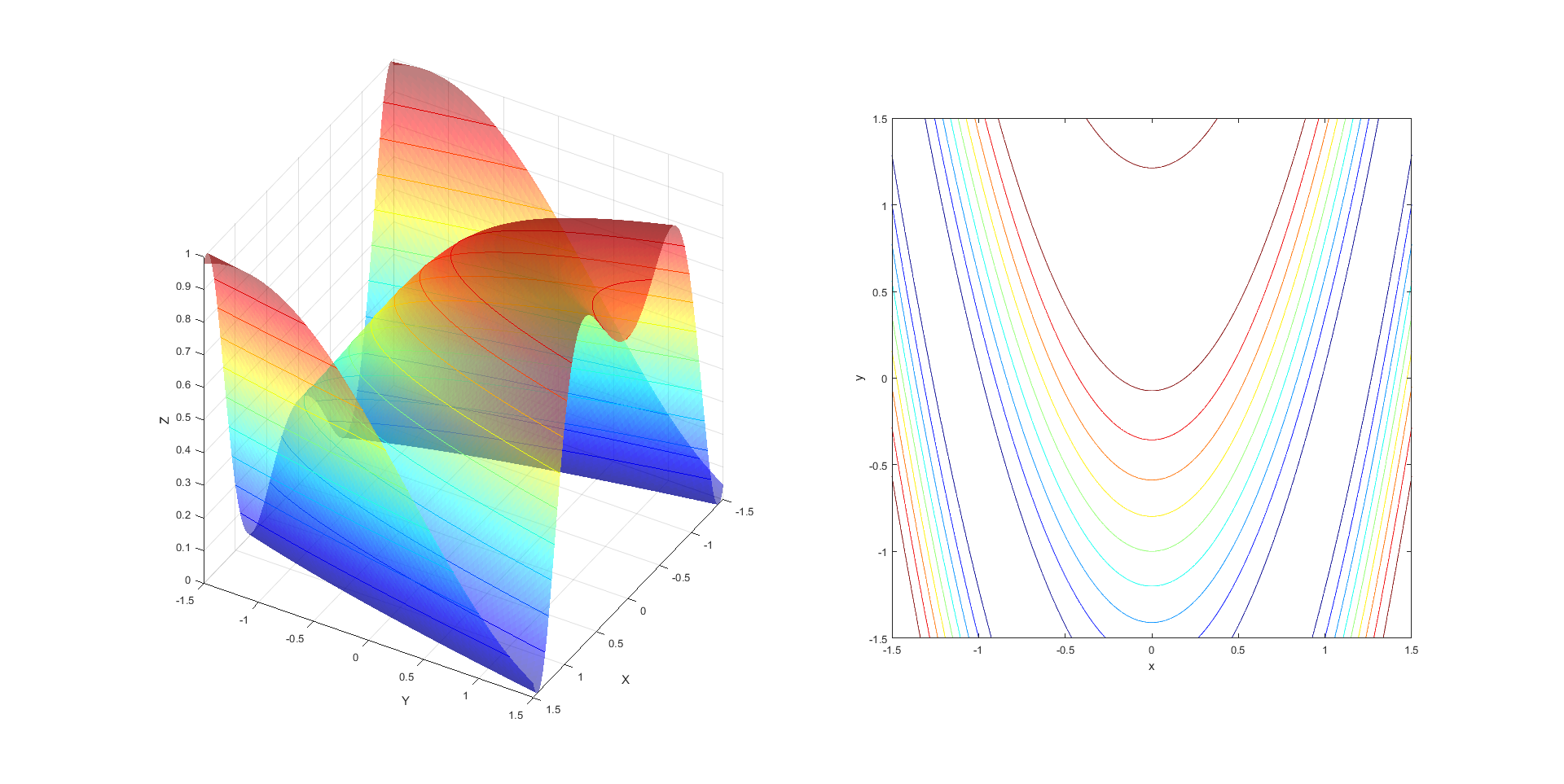
Als je zelf met colormap aan de slag bent gegaan dan zou je bijvoorbeeld het volgende gedaan kunnen hebben:

>> x = linspace(-3,3,500);
>> y = linspace(-3,3,500);
>> [x,y] = meshgrid(x,y);
>> z = 0.5.*(1-sin(2.*x.^2-y-1));
>> fig = figure('Color','White');
>> ax1 = subplot(1,2,1);
>> surf(x,y,z,'EdgeColor','none','FaceAlpha',0.5)
>> % Definitie van een 256x3 matrix met R,G en B waarden.
>> C = [linspace(0.5,1,256)', linspace(0.6,0.2,256)', linspace(0,1,256)']; 
>> colormap(C)
>> hold on
>> contour3(x,y,z)
>> xlabel('X')
>> ylabel('Y')
>> zlabel('Z')
>> xlim([-1.5,1.5])
>> ylim([-1.5,1.5])
>> zlim([0,1])
>> view(120,35)
>> ylim([-1.5,1.5])
>> ax2 = subplot(1,2,2);
>> contour(x,y,z,'Parent',ax2);
>> colormap(C)
>> xlabel('x')
>> ylabel('y')
>> xlim([-1.5,1.5])
>> ylim([-1.5,1.5])
>> axis square

Dit geeft het volgende resultaat:

Opdracht 2

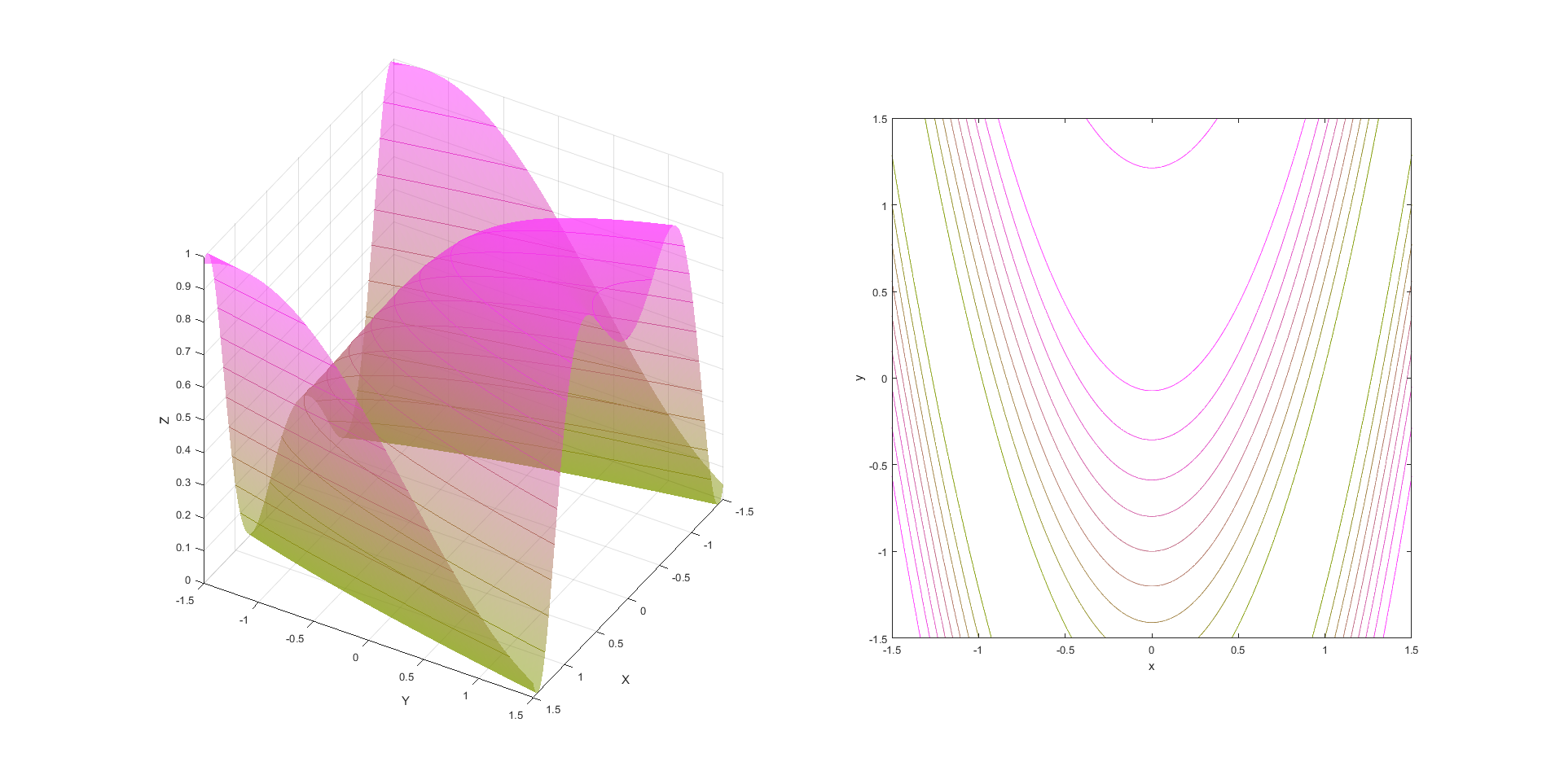
Om de grafiek van de geparametriseerde kromme \[f(t)=(t\cos t, t\sin t, \tfrac{1}{5}t)\] op het interval \([0,50]\) te plotten doen we het volgende:

>> t =  linspace(0,50,500);
>> xt =  t.*cos(t);
>> yt =  t.*sin(t);
>> zt =  0.2.*t;
>> fig = figure('Color','White');
>> plot3(xt,yt,zt,'r','LineWidth',3)
>> grid on
>> xlim([-60,60])
>> ylim([-60,60])
>> zlim([0,10])
>> ax = gca;
>> ax.XTick = [-60:20:60];
>> ax.YTick = [-60:20:60];
>> ax.ZTick = [0:2:10];
>> view(30,30)

Het resultaat: