Complex numbers: The complex plane
 Complex numbers as points in a plane
Complex numbers as points in a plane
The real numberline Recall that the real numbers can be presented as points on a number line. You associate one special point \(O\) on a line with the number \(0\) and a special point \(U\) right with the number \(1\). Then you let points left and right of it correspond to negative and positive numbers, respectively, in such a way that a number \(x\) corresponds with the point \(X\) of \(O\) on the line such that the length ratio \(|OX|\div |OU|\) is equal to the absolute value \(|x|\). A real number is thus represented as a point on the number line on a certain directed distance from the point corresponding to the number \(0\) .
![]()
The complex plane In a similar way we can represent a complex number geometrically as a point in a plane at directed distances from the point corresponding to the number \(0\). The reason that we use a plane is that on the number line there is simply no room for imaginary numbers. The key to the geometrical representation of complex numbers lies in the fact that each complex number is defined by two real numbers, namely the real and imaginary part. We can create a number line for each of these two real ingredients, but it is much more practical to give these number lines the same scale, to let them be perpendicular to each other stand, and to let the zeros on the number lines coincide in such a way that they form the coordinate axes of a coordinate plane. What we do is actually associating the complex unit \(i\) with the point \(I\) that you obtain by rotating \(U\) 90 degrees (counter-clockwise).
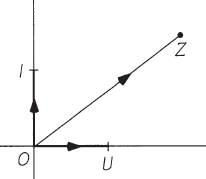
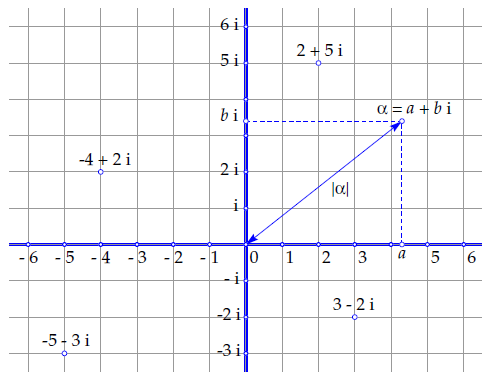
A number such as \(2\,\mathrm{i}\) then corresponds with the point that you get out of \(I\) by marking out twice the standardt length unit on the so-called imaginary axis. So we have two axes in a coordinate plane: the real axis represents the real number and the imaginary axis represents the imaginary numbers. An arbitrary complex number \(z=x+y\,\mathrm{i}\) then corresponds to the point \((x,y)\) in the coordinate plane. In this context, we speak of the complex plane. Other terms are Gauss plane and Argand diagram. The figure below shows a number of points in the complex plane with matching complex number; More examples can be viewed below.
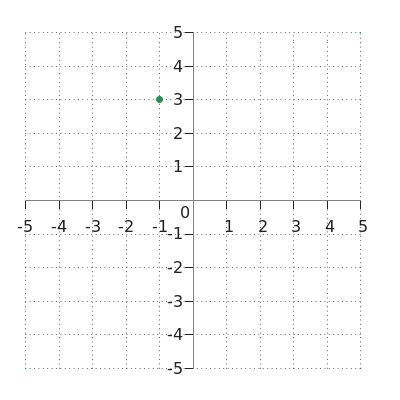
In the below figure the requested point for the complex number \(z\) is colored green.
Some operations with complex numbers are easy to translate into geometric operations in the complex plane.
- Taking the real part of a complex number corresponds with projecting the point on the real axis.
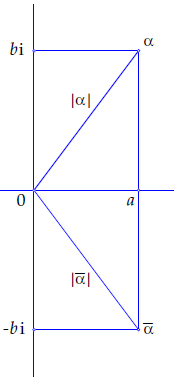
- Complex conjugation corresponds with the reflection of the point in the real axis, as illustrated below.
Mathcentre video
Argand Diagram (6:06)


