Complex numbers: The complex plane
 Complex numbers as vectors
Complex numbers as vectors
Geometric calculations with complex numbers is easier if you do not see complex numbers as points in the complex plane but as vectors.
You can visualize a vector in a coordinate plane as an arrow from a starting point to an terminal point. Parallel arrows in the same direction and with the same magnitude represent the same vector. We speak of a position vector if the starting point is equal to the origin of the coordinate system. For vectors, you can define a sum and difference; the below dynamic figures illustrate this.
Addition and subtraction of vectors Two position vectors add up to each other and the result is again a position vector, which is obtained through the construction of a parallelogram:
Move \(\vec{v}\) and/or \(\vec{w}\) to see how addition of position vectors goes.
Two position vectors can be subtracted from each other and the result is again a position vector, which is obtained through the construction of a parallelogram:
Move \(\vec{v}\) and / or \(\vec{w}\) to see how subtraction of position vectors goes.
A position vector \(\vec{v}\) with endpoint \((v_1,v_2)\) is often denoted as \(\begin{pmatrix} v_1 \\ v_2\end{pmatrix}\) .
The following rule shows in this notation that the addition of vectors goes componentwise.
If \(\vec{v}=\!\!\begin{pmatrix} v_1 \\ v_2\end{pmatrix}\) and \(\vec{w}=\!\!\begin{pmatrix} w_1 \\ w_2\end{pmatrix}\) then \(\vec{v}+\vec{w} = \!\!\begin{pmatrix} v_1+w_1 \\ v_2+w_2\end{pmatrix}\) .
Let us now consider what vectors and complex numbers have to do with each other.
Addition and subtraction of complex numbers in a geometrical perspective In the complex plane one can link any complex number \(\alpha\) with a position vector by drawing an arrow from the origin to the point \(\alpha\) in the complex plane. This position vector can also be represented by a vector ithat starts in an arbitrary point \(\beta\) start and goes to the point \(\alpha+\beta\); the points \(0,\) \(\alpha,\) \(\beta\) and \(\alpha+\beta\) form a parallelogram. See the below figure.
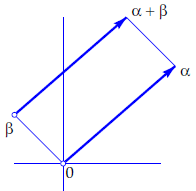
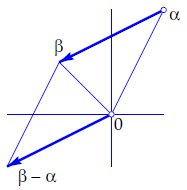
The vector representation of complex numbers is convenient because the addtion of complex numbers corresponds with the addition of vectors. The vector representation is also useful for visualizing the differene \(\beta-\alpha\) of two complex numbers \(\alpha\) and \(\beta\): \(\beta-\alpha\) is the position vector that matches the arrow from \(\alpha\) to \(\beta\). Again, a parallelogram can be used:
Operations with complex numbers can regularly be interpreted in a geometric sense. Below is what happens when you multiply a complex number, matching the vector \(\vec{v}\), with \(\mathrm{i}\). Move \(\vec{v}\) and explore what the geometric interpretation of complex multiplication by \(\mathrm{i}\) is in the complex plane.
Indeed, multiplication with the imaginary unit \(\mathrm{i}\) in the complex plane means geometrically a rotation counter-clockwise in about 90 degrees.


