Complex numbers on the unit circle

Complex numbers: The complex plane

Complex numbers on the unit circle

Recall that the unit circle is defined as the circle with radius $1$ and origin as center. We will now consider complex numbers lying in the complex plane on the unit circle.

Each point on the unit circle has coordinates that can be written as $(\cos\varphi,\sin\varphi)$ , where $\varphi$ is the oriented angle of the radial line (the connecting line of the point with the origin) to the positive $x$ axis. Here we use radians, and the angle is uniquely determined up to an integer multiple of $2\pi$ .

Written as a complex number, a point on the unit circle can always be written in the form

$z=\cos\varphi + \mathrm{i} \sin\varphi$

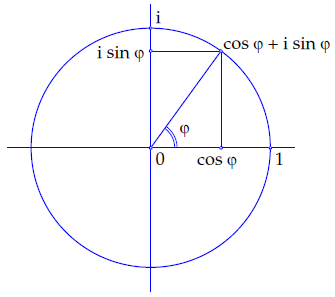
unit circle in the complex plane

Note that indeed for such a number holds

$|\cos\varphi + \mathrm{i} \sin\varphi|=\sqrt{\cos^2\varphi +\sin^2\varphi}=\sqrt{1}=1$

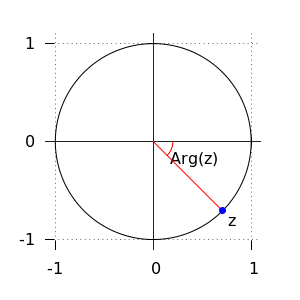
The angle $\varphi$ of the complex number $z=\cos\varphi + \mathrm{i} \sin\varphi$ is called the argument of $z$ and is dentoed as $\mathbf{arg}(z)$ . The argument is unique up to integer multiples of $2\pi$ . You can for any complex number find a unique angle in the interval $(-\pi,\pi]$ . This value, greater than $-\pi$ and less than or equal to $\pi$ , is called the principal value of the argument of $z$ and we write $\mathbf{Arg}(z)$ .

Calculate exactly the principal value of the argument of the complex number $z=-\tfrac{1}{2}\!\sqrt{3}-\tfrac{1}{2}\,\mathrm{i}$ .

$z=-\tfrac{1}{2}\!\sqrt{3}-\tfrac{1}{2}\,\mathrm{i}$ then

$z=\cos(-\tfrac{5}{6}\!\pi) + \mathrm{i}\sin(-\tfrac{5}{6}\!\pi)$ and we have he following situation in the complex plane:

$\begin{aligned} \mathrm{arg}(z)&=-\tfrac{5}{6}\!\pi+2k\pi\quad \text{for integers }k\\ \mathrm{Arg}(z)&=-\tfrac{5}{6}\!\pi\end{aligned}$

New example

With the calculation rules for trigonometric functions we can now figure out how multiplication of two complex numbers on the unit circle yields a new complex number on the unit circle and derive a formula for this product.

The product of two numbers $z_1$ and $z_2$ on the unit circle is another number on the unit circle, and thatis the number whose argument is equal to the sum of the arguments of $z_1$ and $z_2$ .

In symbolic language:
If

$z_1=\cos\varphi_1 + \mathrm{i} \sin\varphi_1\qquad\text{and}\qquad z_2=\cos\varphi_2 + \mathrm{i} \sin\varphi_2$ then

$z_1z_2=\cos(\varphi_1+\varphi_2) + \mathrm{i} \sin(\varphi_1+\varphi_2)$

$z_1=\cos\varphi_1 + \mathrm{i} \sin\varphi_1\qquad\text{and}\qquad z_2=\cos\varphi_2 + \mathrm{i} \sin\varphi_2$ then

$\begin{aligned}z_1z_2&= \bigl(\cos\varphi_1 + \mathrm{i} \sin\varphi_1\bigr)\bigl(\cos\varphi_2 + \mathrm{i} \sin\varphi_2\bigr) \\ \\ &= \bigl(\cos\varphi_1\cos\varphi_2 - \sin\varphi_1\sin\varphi_1\bigr)+\mathrm{i}\bigl(\cos\varphi_1\sin\varphi_2+\sin\varphi_1\cos\varphi_2\bigr)\\ \\ &= \cos(\varphi_1+\varphi_2) + \mathrm{i} \sin(\varphi_1+\varphi_2) \end{aligned}$ The first step is to expand brackets, and the second step is the application of the following trigonometric calculation rules

$\begin{aligned} \cos(\varphi_1+\varphi_2)&=\cos\varphi_1\cos\varphi_2 - \sin\varphi_1\sin\varphi_1\\ \\ \sin(\varphi_1+\varphi_2)&= \cos\varphi_1\sin\varphi_2+\sin\varphi_1\cos\varphi_2\end{aligned}$

For the quotient of complex numbers on the unit circle holds:

The quotient $\dfrac{z_1}{z_2}$ of two numbers on the unit circle is another number on the unit circle, and thatis the number whose argument is equal to the difference of the arguments of $z_1$ and $z_2$ .

In symbolic language:
If

$z_1=\cos\varphi_1 + \mathrm{i} \sin\varphi_1\qquad\text{and}\qquad z_2=\cos\varphi_2 + \mathrm{i} \sin\varphi_2$ then

$\frac{z_1}{z_2}=\cos(\varphi_1-\varphi_2) + \mathrm{i} \sin(\varphi_1-\varphi_2)$