Complex cube roots

Complex numbers: Roots and polynomials

Complex cube roots

We already know that complex square roots exist, but we can go a step further and introduce the cube roots. But first an example.

What could $\sqrt[3]{-1}$ be? We want to solve the equation $z^3=-1$ in the set of complex numbers. For this we first write $-1$ in polar form: $-1 = e^{\pi\,\mathrm{i}+2\,k\,\pi\,\mathrm{i}}$ for integers $k$ . We also write $z$ in polar form, say $z=r\, e^{\,\mathrm{i}\,\varphi}$ Then: $z^3=r^3\, e^{\,\mathrm{i}\,3\varphi}$ So we must find real numbers $r>0$ and $\varphi$ in the interval $(-\pi, \pi]$ such that $r^3=1\qquad\text{and}\qquad 3\varphi=\pi+2k\pi$ Without the restriction of $\varphi$ to the interval $(-\pi, \pi]$ we find $r=1\quad\text{and}\quad \varphi=\tfrac{1}{3}\pi+\tfrac{2}{3}k\,\pi$ for integers $k$ . The solutions within the set of restricted values of $\varphi$ are: $[r=1,\phi= \tfrac{1}{3}\pi]\quad\text{or}\quad [r=1,\varphi= \pi]\quad\text{or}\quad [r=1,\varphi= -\tfrac{1}{3}\pi]$ We have found complex solutions to the equation in polar form $z^3=-1$ ; we can also write them down as $z=e^{(\tfrac{1}{3}\pi+\!\tfrac{2}{3}k\,\pi)\,\mathrm{i}}\quad\text{for }k=0, 1, 2$ For other integer values of $k$ we always get one of these solution because of the periodicity of the complex exponential function. In standard form we have the following solutions: $z=\cos\bigl(\tfrac{1}{3}\pi+\tfrac{2}{3}k\,\pi\bigr)+ \cos\bigl(\tfrac{1}{3}\pi+\tfrac{2}{3}k\,\pi\bigr)\mathrm{i}\quad\text{for }k=0, 1, 2$ For $k=1$ we have a real solution $-1$ . As principal value of $\sqrt[3]{-1}$ we choose in this case $k=0$ and thus the solution $z=e^{\tfrac{1}{3}\pi\,\mathrm{i}}=\tfrac{1}{2}+\mathrm{i}\,\tfrac{1}{2}\sqrt{3}$ .

The following picture shows where the solutions are on the unit circle:

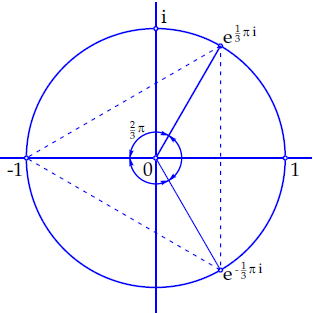
cube root

The points that correspond to the complex cube roots of $-1$ form the vertices of an equilateral triangle with the origin as center. The radii of the three cube roots of $-1$ are separated by the angle $\tfrac{2}{3}\pi$ .

The general case is similar.

For any complex number $z$ we can define the complex cube root in polar form: $\begin{aligned}\sqrt[3]{z}&=\sqrt[3]{|z|}\cdot e^{\,\mathrm{i}\tfrac{1}{3}\mathrm{arg}(z)}\\ \\ \text{principal branch of }\sqrt[3]{z}&=\sqrt[3]{|z|}\cdot e^{\,\mathrm{i}\tfrac{1}{3}\mathrm{Arg}(z)}\end{aligned}$ In terms of the complex exponential function and complex logarithm we can simply define the complex cube root function as $\sqrt[3]{z}=e^{\tfrac{1}{3}\ln(z)}$

So, if $z=r\cdot e^{\,\mathrm{i}\,\varphi}$ , with $r>0$ and $-\pi<\varphi\le\pi$ , then it the principal value of $\sqrt[3]{z}$ is equal to $\sqrt[3]{r}\cdot e^{\,\mathrm{i}\tfrac{1}{3}\varphi}$ .

If want to solve the equation $z^3=1$ in $\mathbb{C}$ , you can best write the solution as $z=\sqrt[3]{1}$ , at least when you keep in mind this it actually denotes the following three solutions: $z=e^{0\,\ii}=1$ , $z=e^{\tfrac{2}{3}\pi\,\ii}=-\tfrac{1}{2}+\tfrac{1}{2}\sqrt{3}\,\ii$ and $z=e^{\tfrac{4}{3}\pi\,\ii}=-\tfrac{1}{2}-\tfrac{1}{2}\sqrt{3}\,\ii$ . After all, $\arg(1)=2k\pi\ii$ for integers $k$ .