Complex numbers: Roots and polynomials
 N-th roots of complex numbers
N-th roots of complex numbers
We already know that complex square roots and cube roots exist and then the step to \(n\)throots of compelx numbers with \(n\gt 3\) not so big anymore. The general case will go in the same way.
Suppose \(n\) is a natural number greater than or equal to 2.
Any complex number \(z=r\cdot e^{\,\mathrm{i}\,\varphi}\) with \(r=|z|>0\) has exactly \(n\) \(n\)th roots, namely \[\sqrt[n]{z}=e^{(\tfrac{1}{n}\pi+\tfrac{2}{n}k\,\pi)\,\mathrm{i}}\quad\text{for }k=0,1,\ldots,n-1\]
The complex nth root For any complex number \(z\) we can define the complex \(n\)th root in polar form: \[\begin{aligned}\sqrt[n]{z}&=\sqrt[n]{|z|}\cdot e^{\,\mathrm{i}\tfrac{1}{n}\mathrm{arg}(z)}\\ \\ \text{principal branch of }\sqrt[n]{z}&=\sqrt[n]{|z|}\cdot e^{\,\mathrm{i}\tfrac{1}{n}\mathrm{Arg}(z)}\end{aligned}\] In terms of the complex exponential function and logarithm, we can simply define the complex root function as \[\sqrt[n]{z}=e^{\tfrac{1}{n}\ln(z)}\]
So, if \(z=r\cdot e^{\,\mathrm{i}\,\varphi}\), with \(r>0\) and \(-\pi<\varphi\le\pi\), then the principal value of \(\sqrt[n]{z}\) is equal to \(\sqrt[n]{r}\cdot e^{\,\mathrm{i}\tfrac{1}{n}\varphi}\) .
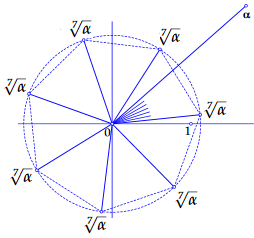
Below are the seven 7th roots \(\sqrt[7]{\alpha}\) of \(\alpha=1.7+1.5\,\ii\) drawn.
The following holds: \[\begin{aligned}|\alpha|&=\sqrt{1.7^2+1.5^2}\approx 2.267\\ \arg(\alpha)&=\arctan\bigl(\frac{1.5}{1.7}\bigr)+2k\pi\approx 0.723+2k\pi\quad\text{for integers }k\tiny.\end{aligned}\] So \[\begin{aligned}\left|\sqrt[7]{\alpha}\right|&=\sqrt[7]{\left|\alpha\right|}\approx 1.124\\ \arg(\sqrt[7]{\alpha})&=\tfrac{1}{7}\arg(\alpha)\approx 0.103+\tfrac{2k\pi}{7}\quad\text{for }k=0,1,\dots 6\tiny.\end{aligned}\] In summary: \[\sqrt[7]{1.7+1.5\,\ii}\approx 1.124\,e^{(0.103+\frac{2k\pi}{7})\,\ii}\quad\text{for }k=0,1,\dots 6\tiny.\] All drawn roots can claim the format \(\sqrt[7]{\alpha}\), but in the first quadrant of the complex plane is a special root (lying closest to \(1\)) that we call the principal value of the 7th root.