Consider the following two uncoupled differential equations of exponential growth \[\frac{\dd x}{\dd t}=x,\qquad \frac{\dd y}{\dd t}=2y\] with initial values \[x(0)=x_0,\qquad y(0)=y_0\] The equations are not connected with each other because each parameter \(x\) and \(y\) only occurs in a single equation. We can solve any individual initial value problem: \[x(t)=x_0\cdot e^t,\qquad y(t)=y_0\cdot e^{2t}\]

Equilibrium There is an equilibrium when \[\frac{\dd x}{\dd t}=0\quad\text{and}\quad \frac{\dd y}{\dd t}=0\tiny.\] In this particular case, the only equilibrium is the solution \(x=0\) and \(y=0\).

No equilibrium In the figure below, the solutions curves for \(x_0=1\) and \(y_0=1\) have been drawn separately in a \(x\)-\(t\) diagram and \(y\)-\(t\) diagram, respectively, together with a diagram in which we can see how \(x\) and \(y\) simultaneous change depending on time \(t\). In the latter diagram had been drawn a parameter curve \(t\mapsto \bigl(x(t), y(t)\bigr)\) in the two-dimensional plane.

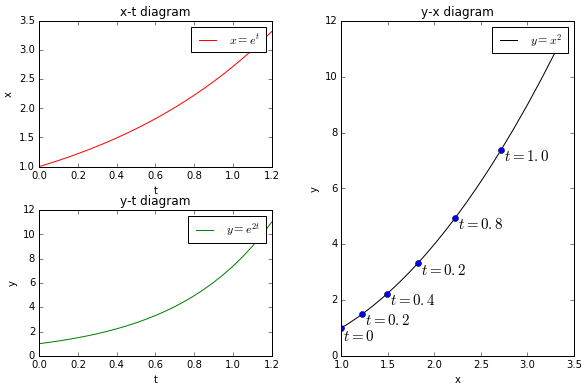
In this particular case, the solutions are \[x=e^t,\qquad y=e^{2t}\] and we have \[y=e^{2t}=(e^t)^{2}=x^2\] The last equation is obtained by eliminating \(t\) from the two solutions \(x=e^t\) and \(y=e^{2t}\).

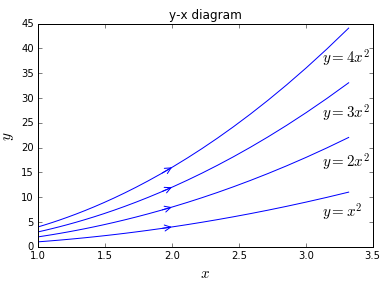
We can generalize this particular case for different initial conditions: Elimination of \(t\) from \(x=x_0e^t\) and \(y=y_0e^{2t}\) gives \[y=y_0(e^t)^{2}=y_0\left(\frac{x}{x_0}\right)^2=\left(\frac{y_0}{x_0^2}\right)x^2=\alpha x^2\] Each pair of initial values \((x_0,y_0)\) leads for the given differential equation to a parabola in the \(xy\)-plane that passes through the point \((x_0,y_0)\). Below we draw the graphs through the points \((1,1), (1,2), (1,3)\) and \((1,4)\). The arrows indicate the direction in which the curve \(y(x)\) runs with increasing time \(t\).

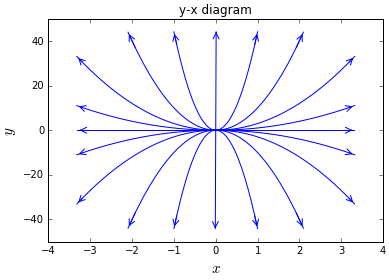
In the figure below have been drawn several curves \(y(x)\) in the \(xy\)-plane corresponding with various initial values (positive, negative, and equal to zero). They are always parts of a parabola or a straight line starting from the origin. A piece of a straight line is obtained in case one of the derivatives \(\dfrac{\dd x}{\dd t}\) or \(\dfrac{\dd y}{\dd t}\) is equal to \(0\), that is, when one of the functions \(x\) or \(y\) equals \(0\).

Interlude: vectors in a plane For the rest of this topic, it is convenient to introduce planar vectors and agree upon a suitable notation for this.

A vector is defined as an arrow in the plane or 3D space with a certain direction and length. In other words, a vector is a segment with a direction; the placement of the vector in the plane or space is not of interest.

The norm or length of the vector is the length of the segment. The length of a vector \(\vec{v}\) is usually denoted as \(\lVert\vec{v}\rVert\).

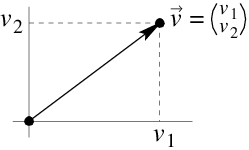
When we drag a vector so that its starting point lies elsewhere, but without changing the direction and length, we can consider this new arrow as a representative of the same vector. Thus, we can focus on vectors which start at the origin of the coordinate system, and these so-called position vectors are then uniquely defined by their end points. We often denote a position vector \(\vec{v}\) with end point \((v_1,v_2)\) as a column vector \( \begin{pmatrix} v_1 \\ v_2\end {pmatrix} \). The individual coordinates \(v_1\) and \(v_2\) are called the components of the vector \(\vec{v}\).

The pair of uncoupled differential equations in our example can be written in vector notation: \[\cv{\frac{\dd x}{\dd t} \\ \frac{\dd y}{\dd t}} =\cv{x \\ 2y}\qquad\text{with}\qquad \cv{x(0)\\y(0)}=\cv{x_0 \\ y_0}\] The column vector with the derivatives is also written as a derivative of a column vector. In this example, we get:
\[\frac{\dd}{\dd t} \cv{x\\ y} =\cv{x \\ 2y}\qquad\text{met}\qquad \cv{x(0)\\y(0)}=\cv{x_0 \\ y_0}\]

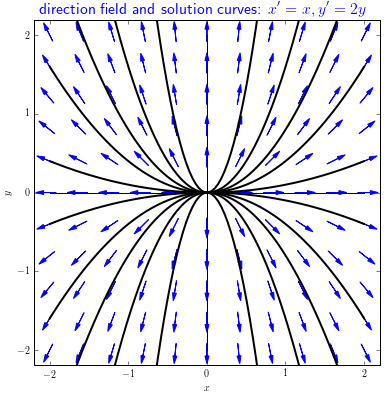
Direction Field, solution curves and phase portrait In the example \[\frac{\dd x}{\dd t}=x,\qquad \frac{\dd y}{\dd t}=2y\] with initial values \[x(0)=x_0,\qquad y(0)=y_0\] we already know how to draw line elements fields for each of the two differential equations. For \(\frac{\dd x}{\dd t}=x\) you draw at every point \((t,x)\) in the \(tx\)-plane a line segment with slope piece \(x\) and centred about the point. This is a line segment for which the direction is equal to a multiple of the vector \(\cv{\frac{\dd x}{\dd t}\\1 }=\cv{x \\ 1}\). For \(\frac{\dd y}{\dd t}=2y\) you draw at any point \((t,y)\) in \(ty\) plane a line segment with slope \(2y\) and centred about the point. This is a line segment for which the direction is equal to a multiple of the vector \(\cv{\frac{\dd y}{\dd t}\\ 1}=\cv{2y \\ 1}\). In both cases, the line elements indicate the direction in which the solution curves go through the chosen point in the \(x\)-\(t\) or \(y\)-\(t\) plane.

\(\phantom{x}\)

But what if we consider \(y\) as a function of \(x\)? The chain rule for differentiating functions informs us: \[\frac{\dd y}{\dd t}=\frac{\dd y}{\dd x}\cdot \frac{\dd x}{\dd t}\] So \[\frac{\dd y}{\dd x}=\frac{\dfrac{\dd y}{\dd t}}{\dfrac{\dd x}{\dd t}}\quad(=\frac{2y}{x} \text{ in this example})\] In other words, the slope at the point \((x,y)\) in the \(xy\)-plane is equal to the quotient of the derivatives of the two functions \(x\) and \(y\) to time \(t\), and in this example equal to \(\frac{2y}{x}\). We can visualize this by a line segment whose direction is equal to a multiple of the vector \(\cv{x \\ 2y}\). Instead of a line segment, you can also draw a vector of which the direction of the arrow indicates the direction in which the parameter curve goes with increasing time \(t\). By default and for convenience, the segment or the arrow is not centred about the corresponding point, but this point is the starting point of the line segment or vector.

This brings us to the concept of direction field, also known as vector field called, in the given system of first-order differential equations: you draw at each point \((x,y)\) a multiple of the vector \(\cv{x \\ 2y}\), for example, a vector having the same direction, but length 1 (a so-called normalized vector ). A parameter curve through a certain point is obtained by 'following the arrows', that is, by 'going with the flow'.

The figure below shows a direction field and several solution curves for \[\frac{\dd x}{\dd t}=x,\qquad \frac{\dd y}{\dd t}=2y\] The direction field is called a phase portrait of the differential equations if we would indicate with an open circle at the origin \((x_0,y_0)=(0,0)\) that this point is a repelling equilibrium. The \(xy\) plane is called the phase plane in this context.