Beschouw de volgende twee ongekoppelde differentiaalvergelijkingen van exponentiële groei

$$\frac{\dd x}{\dd t}=x,\qquad \frac{\dd y}{\dd t}=2y$$ met beginwaarden $$x(0)=x_0,\qquad y(0)=y_0$$ De vergelijkingen zijn niet met elkaar verbonden omdat elke grootheid $x$ en $y$ maar in één vergelijking voor komt. We kunnen elk beginwaardeprobleem afzonderlijk oplossen: $$x(t)=x_0\cdot e^t,\qquad y(t)=y_0\cdot e^{2t}$$

Evenwicht Er is sprake van een evenwicht als

$$\frac{\dd x}{\dd t}=0\quad\text{en}\quad \frac{\dd y}{\dd t}=0\tiny.$$ In dit geval is het enige evenwicht de oplossing $x=0$ en $y=0$.

Geen evenwicht In onderstaande figuur zijn de oplossingen voor $x_0=1$ en $y_0=1$ afzonderlijk in een $x$-$t$ diagram respectievelijk $y$-$t$ diagram getekend, samen met een diagram waarin we zien hoe $x$ en $y$ simultaan veranderen afhankelijk van de tijd $t$. Het gaat in het laatste geval om een parameterkromme $t\mapsto \bigl(x(t), y(t)\bigr)$ in het platte vlak.

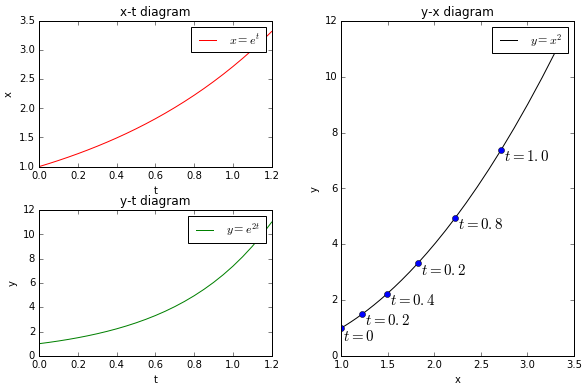
In dit speciale geval zijn de oplossingen namelijk

$$x=e^t,\qquad y=e^{2t}$$ en hebben we $$y=e^{2t}=(e^t)^{2}=x^2$$ De laatste vergelijking is verkregen door eliminatie van $t$ uit de twee oplossingen $x=e^t$ en $y=e^{2t}$.

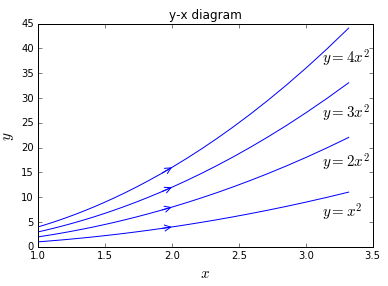
We kunnen dit speciale geval generaliseren voor verschillende beginwaarden: Eliminatie van $t$ uit $x=x_0e^t$ en $y=y_0e^{2t}$ geeft

$$y=y_0(e^t)^{2}=y_0\left(\frac{x}{x_0}\right)^2=\left(\frac{y_0}{x_0^2}\right)x^2=\alpha x^2$$ Elk paar van beginwaarden $(x_0,y_0)$ levert dus bij de gegeven differentiaalvergelijking een parabool in het $xy$-vlak op die door het punt $(x_0,y_0)$ gaat. Hieronder tekenen we de grafieken door de punten $(1,1), (1,2), (1,3)$ en $(1,4)$. De pijlen geven aan in welke richting de kromme $y(x)$ loopt bij toenemende tijd $t$.

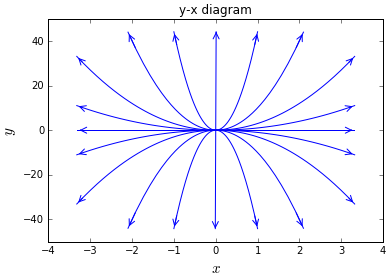
In onderstaande figuur zijn verschillende krommen $y(x)$ getekend in het $xy$-vlak horende bij verschillende beginwaarden (positief, negatief en gelijk aan nul). Het zijn steeds stukken van een parabool of rechte lijn startend vanuit de oorsprong. Een stuk van een rechte lijn krijg je wanneer één van de afgeleiden $\dfrac{\dd x}{\dd t}$ of $\dfrac{\dd y}{\dd t}$ gelijk aan $0$ is, oftewel wanneer één van de functies $x$ of $y$ gelijk is aan $0$.

Intermezzo: vectoren in een vlak Voor het vervolg is het handig om vectoren in het platte vlak te introduceren en hiervoor een geschikte notatie af te spreken.

Onder een vector verstaan we een pijl in het vlak of een 3D-ruimte met een zekere richting en lengte. Met andere woorden: een vector is een lijnstuk met een richting; de plaatsing van de vector in het vlak of de ruimte is niet van belang.

De norm of gewoon lengte van de vector is de lengte van het lijnstuk. De lengte van een vector $\vec{v}$ wordt meestal genoteerd als $\lVert\vec{v}\rVert$.

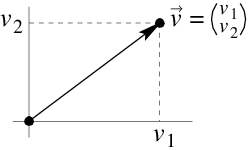
Verslepen we een vector zodat zijn beginpunt elders komt te liggen (maar richting en lengte onveranderd blijven), dan beschouwen we deze nieuwe pijl als een representant van dezelfde vector. We kunnen dus focussen op vectoren die starten in de oorsprong van het assenstelsel en deze zogenaamde plaatsvectoren worden dan uniek bepaald door hun eindpunten. Een plaatsvector $\vec{v}$ met eindpunt $(v_1,v_2)$ noteren we vaak als als een kolomvector $\begin{pmatrix} v_1 \\ v_2\end{pmatrix}$. De individuele coördinaten $v_1$ en $v_2$ worden de componenten van de vector $\vec{v}$ genoemd.

Het tweetal ongekoppelde differentiaalvergelijkingen uit ons voorbeeld is ook te schrijven in vectornotatie:

$$\cv{\frac{\dd x}{\dd t} \\ \frac{\dd y}{\dd t}} =\cv{x \\ 2y}\qquad\text{met}\qquad \cv{x(0)\\y(0)}=\cv{x_0 \\ y_0}$$ De kolomvector met de afgeleiden wordt ook geschreven als afgeleide van een kolomvector. In dit voorbeeld krijgen we dan:
$$\frac{\dd}{\dd t} \cv{x\\ y} =\cv{x \\ 2y}\qquad\text{met}\qquad \cv{x(0)\\y(0)}=\cv{x_0 \\ y_0}$$

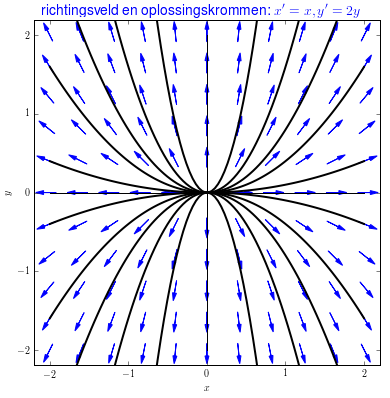
Richtingsveld, oplossingskrommen en faseportret In het voorbeeld

$$\frac{\dd x}{\dd t}=x,\qquad \frac{\dd y}{\dd t}=2y$$ met beginwaarden $$x(0)=x_0,\qquad y(0)=y_0$$ weten we al hoe lijnelementenvelden te tekenen voor elk van de twee differentiaalvergelijkingen. Voor $\frac{\dd x}{\dd t}=x$ teken je in het elk punt $(t,x)$ in het $tx$-vlak gecentreerd een lijnstukje met helling $x$. Dit is een lijnstuk waarvan de richting gelijk is aan een veelvoud van de vector $\cv{\frac{\dd x}{\dd t}\\1 }=\cv{x \\ 1}$. Voor $\frac{\dd y}{\dd t}=2y$ teken je in elk punt $(t,y)$ in het $ty$-vlak gecentreerd een lijnstukje met helling $2y$. Dit is een lijnstuk waarvan de richting gelijk is aan een veelvoud van de vector $\cv{\frac{\dd y}{\dd t}\\ 1}=\cv{2y \\ 1}$. In beide gevallen geven de lijnelementen aan in welke richting de oplossingskrommen door het gekozen punt lopen in het $x$-$t$ of $y$-$t$ vlak.

$\phantom{x}$

Maar hoe zit dat als we $y$ als functie van $x$ beschouwen? De kettingregel voor differentiëren biedt uitkomst:

$$\frac{\dd y}{\dd t}=\frac{\dd y}{\dd x}\cdot \frac{\dd x}{\dd t}$$ Dus: $$\frac{\dd y}{\dd x}=\frac{\dfrac{\dd y}{\dd t}}{\dfrac{\dd x}{\dd t}}\quad(=\frac{2y}{x} \text{ in dit voorbeeld})$$ Met andere woorden: de helling in het punt $(x,y)$ in het $xy$-vlak is gelijk aan het quotiënt van de afgeleiden van de twee functies $x$ en $y$ naar tijd $t$, en in dit voorbeeld gelijk aan $\frac{2y}{x}$. Dit kunnen we visualiseren door een lijnstuk waarvan de richting gelijk is aan een veelvoud van de vector $\cv{x \\ 2y}$. In plaats van een lijnstuk kun je ook een vector tekenen waarvan de pijlrichting aangeeft in welke richting de parameterkromme gaat bij toenemende tijd $t$. Standaard wordt voor het gemak het lijnstuk of de pijl niet gecentreerd rondom het bijpassende punt, maar is dit punt het startpunt van het lijnstuk of de vector.

Dit brengt ons bij het begrip richtingsveld, ook wel vectorveld genaamd, bij het gegeven stelsels van eerste-orde differentiaalvergelijkingen: je tekent in elk punt $(x,y)$ een veelvoud van de vector $\cv{x \\ 2y}$, bijvoorbeeld een vector met dezelfde richting maar lengte 1 (een zogenaamde genormaliseerde vector). Een parameterkromme door een zeker punt krijg je dan door 'de pijltjes te volgen' oftewel door 'met de stroom mee te gaan'.

Onderstaande figuur toont een richtingsveld en enkele oplossingskrommen voor

$$\frac{\dd x}{\dd t}=x,\qquad \frac{\dd y}{\dd t}=2y$$ Het richtingsveld heet een faseportret van de differentiaalvergelijkingen als we nog met een open cirkel in de oorsprong aan zouden geven dat $(x_0,y_0)=(0,0)$ past bij een afstotend evenwicht. Het $xy$ vlak noemen we in deze context het fasevlak.